編程開發中如何實現堆

這篇文章主要介紹了編程開發中如何實現堆，具有一定借鑒價值，感興趣的朋友可以參考下，希望大家閱讀完這篇文章之后大有收獲，下面讓小編帶著大家一起了解一下。

一、堆的概念  

  堆數據結構是一種數組對象，它可以被視為一棵完全二叉樹結構。

  堆結構的二叉樹存儲是：

  最大堆：每個父節點的都大于孩子節點。

  最小堆：每個父節點的都小于孩子節點。

     堆棧中的物體具有一個特性： 最后一個放入堆棧中的物體總是被最先拿出來， 這個特性通常稱為后進先出(LIFO)隊列。 堆棧中定義了一些操作。 兩個最重要的是PUSH和POP。 PUSH操作在堆棧的頂部加入一 個元素。POP操作相反， 在堆棧頂部移去一個元素， 并將堆棧的大小減一。

    在此，用vector容器來實現存儲，vector容器是一個模板類，可以存放任何類型的對象（但必須是同一類對象）。vector對象可以在運行時高效地添加元素，并且vector中元素是連續存儲的。當容量不夠時，它能夠自己去擴容。故我們在push數據時就不用考慮一些其他容量不足等等因素。

二、堆的實現

  通過二叉樹來實現堆的結構。

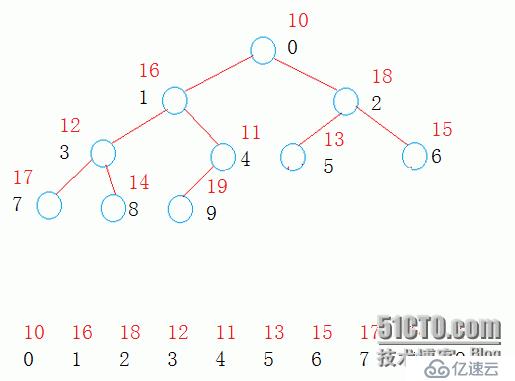
先實現一個compare，如果實現大小堆用對象調其對應類運算符“（）”重載

template<class T>
struct Less
{
	bool operator()(const T& l, const T& r)
	{
		return l < r;
	}
};
template<class T>
struct Big
{
	bool operator()(const T& l, const T& r)
	{
		return l > r;
	}
};

先定義一個堆：

  用模板的模板參數：

   如：當 測試用例為：

      int arr[] = { 12, 10, 43, 23, 22, 45, 67,9 };

 Heap<int,Big>  N(arr, sizeof(arr)/sizeof(arr[0])); 

 當你給定compare為Big時它會按照大堆去排序

 Heap<int,Less>  N(arr, sizeof(arr)/sizeof(arr[0])); 

 當你給定compare為Big時它會按照小堆去排序

template<class T , template<class>  class compare >  //模板的模板參數
class Heap
{

public:
	Heap()
	{}
	Heap(T* a, size_t size)
	{
		_a.reserve(size);
		for (size_t i = 0; i < size; ++i)
		{
			_a.push_back(a[i]);
		}
		//建堆
		
		for (int i = (_a.size() -2)/2; i >= 0; --i)
		{
			_AdjustDown(i);
		}
	    Disp(_a, size);
	}
	//Pop時，先將第一個與最后一個交換，（這樣不至于打亂其他子堆的順序），然后
	//刪除最后一個，再讓它下調重新調整順序
	void Pop()       
	{
		size_t _size = _a.size();
		assert(_size > 0);
		swap(_a[0], _a[_size-1]);
		_a.pop_back();
		_size = _a.size();
		_AdjustDown(0);
		Disp(_a, _size);
	}
	//push一個數據后，讓其上調，以調整順序
	void Push(const T& x)
	{
		_a.push_back(x);
		size_t _size = _a.size();
		_AdjustUp(_size-1);
		Disp(_a, _size);
	}
	T& Top()
	{
		assert(!_a.empty());
	    return _a[0];
	}
	bool empty()
	{
		return _a.size() == 0;
	}
	void Disp(vector<T> a, size_t k)//打印
	{
		for (size_t j = 0; j < k; j++)
		{
			cout << a[j] << " ";
		}
		cout << endl;
	}

在建堆時，首先來定義一個下調函數_AdjustDown（）；用來調整已實現大小堆順序。

 實現思想：

     1、找最后一個非葉子結點

2、如果當前結點的孩子結點左孩子大于右孩子，就讓child指向最大孩子結點（在此必須滿足存在右孩子）

3、如果當前結點小于孩子結點，就交換，下調，將孩子給父親，孩子結點下移

4、不滿足  就break；

	void _AdjustDown(size_t parent)    //     下調
	{
		size_t child = parent * 2 + 1;
		while (child < _a.size())
		{
			compare<T> _com;  
			if ( child + 1 < _a.size()&&_com(_a[child + 1], _a[child]) )
			{
				++child;
			}
			if (_com(_a[child],_a[parent]))
			{
				swap(_a[child], _a[parent]);
				parent = child;
				child = parent * 2 + 1;
			}
			else
			{
				break;
			}
		}
	}

再寫一個上調函數_AdjustUp（）當Push一個數時，讓它上調，以調整整個堆的順序。

實現思想：

     1、上調，傳當前結點，令當前節點為孩子結點，上一結點為父結點，

2、在這里不用考慮左右結點誰大誰小

3、如果孩子結點大于父親結點，交換，上移

4、不滿足  就break；

注意：在此不用考慮左右子數誰大誰小，上調是如果孩子結點比父結點大，那它肯定比兄弟結點大。

void _AdjustUp(size_t child)   //上調
	{
		compare<T> _com;
		size_t parent = (child - 1) / 2;
		while (child > 0)
		{
			if (_com(_a[child], _a[parent]))
			{
				swap(_a[child], _a[parent]);
				child = parent;
				parent = (child - 1) / 2;
			}
			else
			{
				break;
			}
		}
	}

三、優先隊列

template<class T, template<class>  class compare = Big>//利用模板的模板參數
class PriorityQueue  //優先隊列
{
protected:
	Heap<T, compare> _hP;
public:
	void _push(const T& x)
	{
		_hP.Push(x);
	}
	void Pop()
	{
		_hP.Pop();
	}
	T& Top()
	{
		return _hP.Top();
	}
};

測試用例：
PriorityQueue<int,Big> s;
	s._push(3);
	s._push(12);
	s._push(5);
	s._push(78);
	s._push(43);
	s._push(10);
	s._push(32);	

結果會以大堆形式實現為：

如果將測試用例改為：

PriorityQueue<int,Less> s;
	s._push(3);
	s._push(12);
	s._push(5);
	s._push(78);
	s._push(43);
	s._push(10);
	s._push(32);

  結果會以小堆實現 為：

感謝你能夠認真閱讀完這篇文章，希望小編分享的“編程開發中如何實現堆”這篇文章對大家有幫助，同時也希望大家多多支持億速云，關注億速云行業資訊頻道，更多相關知識等著你來學習!