您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“從0手寫一個力導向關系圖的方法教程”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“從0手寫一個力導向關系圖的方法教程”吧!
下圖,是本次要講的項目動態實例:
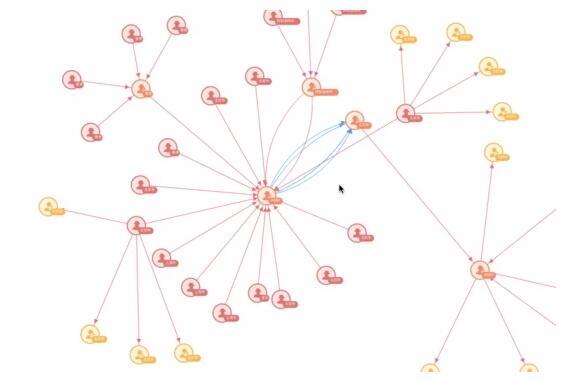
力導向圖大家都不陌生,力導向圖缺少不了力,而在數據量很大的情況下初始化節點以及對節點進行拖動時會導致整個力導圖都在一直在動,密集的情況會更加嚴重,并且本著可以對點更好,靈活的控制,滿足不同的需求,所以打算自己實現一個簡單的力導向圖,并在過程中對碰撞檢測進行一次探索。
整體內容分為兩個部分
鴻蒙官方戰略合作共建——HarmonyOS技術社區
兩點之間多條邊的處理
點的框選
點的刪除
縮略圖
主圖的拖拽、縮放與縮略圖
鴻蒙官方戰略合作共建——HarmonyOS技術社區
碰撞檢測
矩形與矩形的檢測
圓形與圓形
圓形與矩形
點的分配
碰撞后點的移動
拖動
一 使用d3.js 開發力導向圖出現的問題
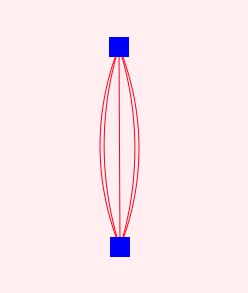
思路為 ,將兩點之間的線進行分組,中間,左右分別為三組,分好組后,當tick 進行渲染時,通過分組內容的數量,對分組內容改變path 的彎曲程度。
拖拽中創建一個矩形框,拖拽后判斷中心點是否在矩形框中則為被框選中. 注: 位置需要與d3 縮放的scale 配合計算
點的刪除實際上 就是把 相關點與線全部刪除, 并且清空畫布后, 重新用刪除后的數據重新繪制。
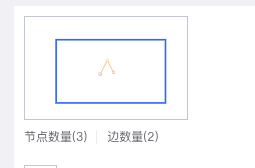
縮略圖目前的邏輯是主圖的最大倍數作為背景,主圖的寬高作為縮略圖視野(藍框)的寬高。因為縮略圖的dom 的寬高是css 定死的,viewbox 是實際寬高,所以給定主圖(正常)的寬高 會自動縮放。在拖拽主圖的點與相應操作時,對縮略圖的點也進行相應的變動,實際上就是在縮略圖中又畫了一遍主圖的內容
/** * @params * width 縮略圖寬度 * height 縮略圖高度 * mainWidth 主圖的寬度 * mainHeight 主圖的高度 * zoomMax 最大縮放比例 * */ thumbSvg.attr('width', width) .attr('height', height).attr('viewBox', () => { // 縮略圖的寬高為 主圖的 最大縮略比例 w = mainWidth * zoomMax; h = mainHeight * zoomMax; // 設置偏移 讓背景圖移至中心,縮略圖與主圖的差/ 2 就是需要移動的距離 x = -(w - mainWidth) / 2; y = -(h - mainHeight) / 2; return `${x} ${y} ${w} ${h}`; }); dragThumb.attr('width', mainWidth) .attr('height', mainHeight);調用主圖的縮放時(zoom) 會得到縮放以及拖拽信息,縮略圖使用拖拽的信息,因為viewbox 的原因,拖拽信息會自動縮放。但是需要注意主圖的縮放會對translate 進行變化 所以需要自己去處理 縮放過程中產生的位移
因為縮放會造成 主圖的 translate 發生變化 與手動拖拽造成的translate 會有差 所以 要扣除縮放造成的偏移
/** * @params * innerZoomInfo 縮略圖的縮放信息 * mainTransform 主圖的縮放信息 * mainWidth,mainHeight 主圖的寬高 */ const { innerZoomInfo, mainWidth, mainHeight, } = this; // 如果傳入的 縮放值與之前記錄的縮放值不一致 則認為發生了縮放 記錄發生縮放后偏移值 if (!innerZoomInfo || innerZoomInfo.k !== mainTransform.k) { this.moveDiff = { x: (mainWidth - innerZoomInfo.k * mainWidth) / 2, //縮放產生的 位移 y: (mainHeight - innerZoomInfo.k * mainHeight) / 2, }; } const { x: diffX, y: diffY } = this.moveDiff; const { x, y, k } = mainTransform; // 主圖偏移以及縮放數據 this.dragThumb .attr('width', mainWidth / k) .attr('height', mainHeight / k) .attr('transform', () => setTransform({ x: -((x - diffX) / k), // 這個地方應該不能直接 除 k 這里的x,y 應該是放大后的x,y應該減去縮放的差值 再 除K y: -((y - diffY) / k), }));矩形與矩形的碰撞是最好檢測的
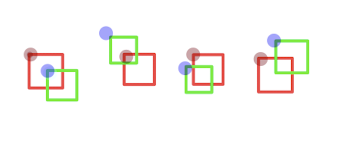
通過上面的圖基本就涵蓋了規則矩形相交的情況 圖可以得知 A:紅色矩形 B:綠色矩形 上下是通過Y,左右是通過X
A.x < B.x + B.width && A.x + A.width > B.x && A.y < B.y + B.h && A.h + A.y > B.y
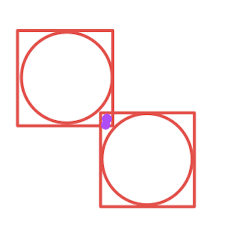
但是如果內部是一個圓形的話,那么如果 紫色的區域則會被判定為碰撞則 則準確性有一定的偏差,需要有圓形的檢測
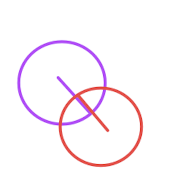
圓形與圓形的邏輯也比較簡單,就是兩點之間的距離小于兩點半徑之和 則為碰撞
var a = dot2.x-dot1.x; var b = dot2.y-dot1.y; return Math.sqrt(a*a+b*b) < a.radius + b.radius;
首先來看 矩形與圓形相交是什么樣,從圖所知矩形與圓形相交,表現為圓點距離矩形最近的點小于圓點半徑 則為相交 那么如何得到圓點距離矩形最近的點
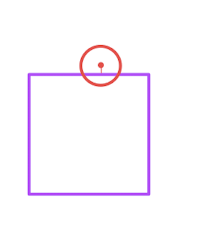
從下圖就知道了 圓點的延伸是圓點邊的一點。crashX = 如果 圓點位于矩形 左側 矩形(rect).x; 右側 = rect.x + rect.w 上下 圓點(circle).x
crashY = 如果 圓點位于矩形 左右 circle.y; 上 rect.y 上下 rect.y + h
那么兩點有了,可以得出兩點之間的距離套用圓與圓的公式
var a = crash.x-dot1.x; var b = crash.y-dot1.y; return Math.sqrt(a*a+b*b) < a.radius;
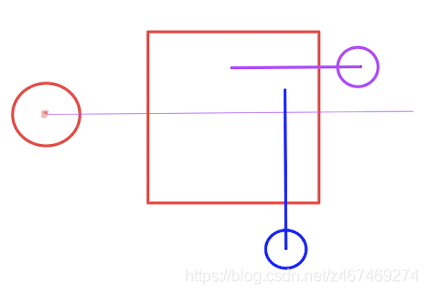
上面就是基本的碰撞邏輯,更復雜的邏輯可以看下面參考文章 [1]

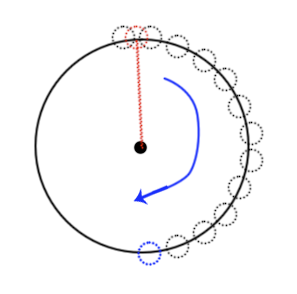
點的位置的分配 就是確定中心點后,將關系最多的點作為中心點,其關系點向四周分散,沒有關系的同級點,則向中心點四周進行分散,其關系點以確定后位置的點的坐標向周圍分散。
根據三角形的正玄、余弦來得值;假設一個圓的圓心坐標是(a,b),半徑為r,角度為d 則圓上每個點的坐標可以通過下面的公式得到
/* * @params * d 角度 * r 半徑長度 */ X = a + Math.cos(((Math.PI * 2) / 360) * d) * r; Y = b + Math.sin(((Math.PI * 2) / 360) * d) * r;
角度可以通過 關系邊進行得到. d = 360/關系邊的數量,確定第一圈點的角度。拿到角度后 ,維持一個所有點坐標的對象,再結合圓形與圓形碰撞檢測,我們就可以遍歷 獲取所有點的坐標了

/* * @params * dotsLocations 所有點的坐標信息 */ initNodes() { const { x: centerX, y: centerY } = this.center; const { distance } = this; const getDeg = (all, now) => 360 / (all - (now || 0)); // 把中心點分配給線最多的點 const centerdot = this.dots[0]; centerdot.x = centerX; centerdot.y = centerY; this.dotsLocations[centerdot.id] = { x: centerX, y: centerY }; this.dots.forEach((dot) => { const { x: outx, y: outy } = dot; if (!outx && !outy) { // 兄弟點 (無關系的點) 默認以中心店的10度進行遍歷 dot = this.getLocation(dot, centerX, centerY,10, distance).dot; } const { x: cx, y: cy } = dot; const dotsLength = dot.relationDots.length; let { distance: innerDistance } = this; // 獲取剩余點的角度 let addDeg = getDeg(dotsLength); dot.relationDots.forEach((relationId, index) => { let relationDot = this.findDot(relationId); if (!relationDot.x && !relationDot.y) { const { dot: resultDot, isPlus, outerR, } = this.getLocation(relationDot, cx, cy, addDeg, innerDistance); if (isPlus) { // 如果第一圈遍歷完畢,則開始以 半徑 * 2 為第二圈開始遍歷 innerDistance = outerR; addDeg = getDeg(dotsLength, index); addDeg += randomNumber(5, 9); //防止第一圈與第二圈的點所生成的角度一致 造成鏈接的線重疊在一起 } relationDot = resultDot; } }); }); }// 分配位置 getLocation(dot, cx, cy, addDeg, distance) { // 由第一張圖 得知 -90度為最上面 從最上面開始循環 let outerDeg = -90; let outerR = distance; const { distance: addDistance } = this; let firsted; // 用于分布完后一周 while (Object.keys(this.checkDotLocation(dot)).length !== 0) { outerDeg += addDeg; if (outerDeg > 360) { // 轉完一圈 隨機生成第二圈的角度再開始對當前點進行定位 addDeg = randomNumber(10, 35); outerDeg = addDeg; if (firsted) { outerR += addDistance; } firsted = true; } const innerLocation = getDegXy(cx, cy, outerDeg, outerR); dot = Object.assign(dot, innerLocation); } this.dotsLocations[dot.id] = { x: dot.x, y: dot.y }; return { dot, isPlus: firsted, outerR, }; } // 碰撞檢測 checkDotLocation(circleA) { let repeat = false; if (!circleA.x || !circleA.y) return true; const { forceCollide } = this; console.log(this.dotsLocations) Object.keys(this.dotsLocations).forEach((key) => { if (key === circleA.id) { return; } const circleB = this.dotsLocations[key]; let isRepeat = Math.sqrt(Math.pow(circleA.x - circleB.x, 2) + Math.pow(circleA.y - circleB.y, 2)) < forceCollide * 2; if(isRepeat)repeat = true; }); return repeat; } }生成時間與D3 的差不多
碰撞后的邏輯呢 簡單的就是已拖動點為圓點,計算碰撞點與圓點的夾角,再通過角度與距離得出碰撞后被碰撞點的x,y的坐標
changeLocation(data, x, y, eliminate) { // 先對原來的點進行賦值 data.x = x; data.y = y; // 對點的坐標進行賦值,使之后的碰撞使用新值進行計算 this.dotsLocations[data.id] = { x, y }; let crashDots = this.checkDotLocation(data); // 獲得所有被碰撞的點 Object.keys(crashDots).forEach((crashId) => { if (eliminate === crashId) return; // 碰撞后的碰撞防止 更改當前拖拽元素 const crashDot = this.findDot(crashId); // 獲取被碰撞的x,y 值 const { x: crashX, y: crashY } = crashDot; // 此處的角度是要移動的方向的角度 let deg = getDeg(crashDot.x,crashDot.y,data.x,data.y); // - 180 的目的是為了 與上面的黑圖角度一致 // 2是碰撞后 移動2個像素的半徑 const {x:endX,y:endY} = getDegXy(crashDot.x, crashDot.y, deg - 180, 2); // 講被碰撞的點作為圓點 改變值 并進行碰撞點的碰撞的碰撞檢測(禁止套娃 ) this.changeLocation(crashDot, endX, endY, data.id); }); }獲取夾角角度
function getDeg(x1,y1,x2,y2){ //中心點 let cx = x1; let cy = y1; //2個點之間的角度獲取 let c1 = Math.atan2(y1 - cy, x1 - cx) * 180 / (Math.PI); let c2 = Math.atan2(y2 - cy, x2 - cx) * 180 / (Math.PI); let angle; c1 = c1 <= -90 ? (360 + c1) : c1; c2 = c2 <= -90 ? (360 + c2) : c2; //夾角獲取 angle = Math.floor(c2 - c1); angle = angle < 0 ? angle + 360 : angle; return angle; }到此實現一個簡單的拓撲圖就搞定了。使用我們自己的force 代替 d3.js 的效果,后期想要什么效果就可以自己再加了 如 拖動主點相關點動,其他關聯點不動的需求。tick方法需要自己手動去調用了
let force = new Force({ x: svgW / 2, y: svgH / 2, distance: 200, forceCollide:30, }); force.nodes(dot); force.initLines(line);這邊的tick 是當 點的xy 發生變化的時候 自己去重新構建點和線。再實際項目中每一次拖動就會構建,會比較卡,可以丟到requestAnimationFrame 去調用
dotDoms.on("mousedown", function (d) { dragDom = { data: d, dom: this, }; }); d3.select("svg").on("mousemove", function (d) { if (!dragDom) return; const { offsetX: x, offsetY: y } = d3.event; if (x < -1 || y < -1 || x >= svgH - 10 || y >= svgH - 10) { //邊界 dragDom = null; return; } force.changeLocation(dragDom.data, x, y); tick(); }); d3.select("svg").on("mouseup", function (d) { dragDom = null; });感謝各位的閱讀,以上就是“從0手寫一個力導向關系圖的方法教程”的內容了,經過本文的學習后,相信大家對從0手寫一個力導向關系圖的方法教程這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。