溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
堆數據結構是一種數組對象,它可以被視為一棵完全二叉樹結構。
堆結構的二叉樹存儲是
最大堆:每個父節點的都大于孩子節點。
最小堆:每個父節點的都小于孩子節點。

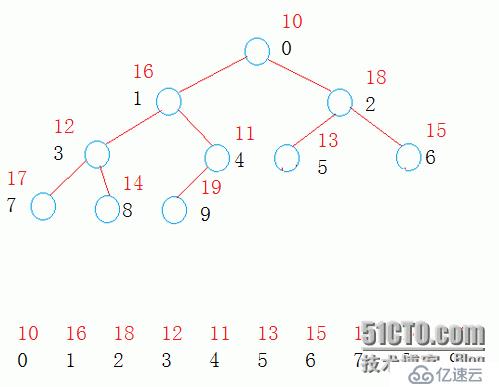
這是一個普通的堆,我們想把它變成最大堆,就必須了解最大堆的特點。然后我們對它進行調整,保證每個父節點的都大于孩子節點。
我們先調整這個二叉樹的一部分,從它的最后一個節點開始調整,圖中紅色箭頭開始調整,如果父節點小于孩子節點,就交換,否則結束。在看下一個節點,一直這樣循環,直到全部調整完。
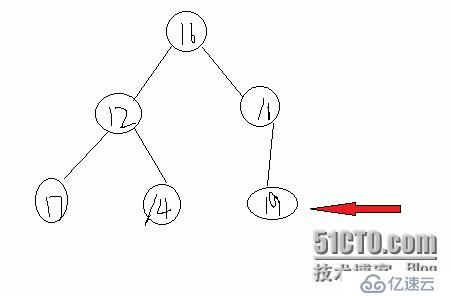
代碼如下:
void _AdjustDown(size_t parent, size_t size)
{
size_t child = 2 * parent + 1;
while (child < size)
{
//child + 1 < size保證是最后一個節點
if (child + 1 < size&&_arr[child] < _arr[child + 1])
{
child++;//孩子節點最大的一個節點
}
//交換
if (_arr[child]>_arr[parent])
{
swap(_arr[child],_arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}如果想把它調整成最小堆,必須符合每個父節點的都小于孩子節點,代碼原理和最大堆相似。
代碼如下:
void _AdjustUp(int child)
{
int parent = (child - 1) / 2;
int size = _arr.size();
while (child > 0)
{
if (_arr[child] > _arr[parent])
{
swap(_arr[child], _arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}下面我給出完整代碼,構造函數用的是調整成大堆。為了讓代碼更簡潔,實現過程借用了庫函數中的vector。
代碼如下:
Heap.h中
#include<assert.h>
#include <vector>
template <class T>
class Heap
{
public:
Heap()
:_arr(NULL)
{}
//構造函數
Heap(const T*arr, size_t size)
{
_arr.reserve(size);
for (size_t i = 0; i < size; i++)
{
_arr.push_back(arr[i]);
}
for (int j = (_arr.size() - 2) / 2; j >= 0; j--)
{
_AdjustDown(j, size);
}
}
//拷貝構造
Heap(const vector<T>& h)
{
_arr.reserve(_arr.size());
for (size_t i = 0; i < _arr.size(); i++)
{
_arr.push_back(h[i]);
}
}
//先儲存在順序表中,在進行下調
void push(const T& x)
{
_arr.push_back(x);
_AdjustUp(_arr.size()-1);
}
//刪除
void pop()
{
size_t size = _arr.size();
assert(size > 0);
swap(_arr[0], _arr[size - 1]);//先把根結點和要刪除的結點交換
_arr.pop_back();//然后刪除
size = _arr.size();
_AdjustDown(0, size);//最后上調
}
//堆是否為空
bool Empty()
{
size_t size = _arr.size();
assert(size >= 0);
return size == 0;
}
//堆的大小
size_t Size()
{
size_t size = _arr.size();
assert(size >= 0);
return size;
}
//訪問根結點
T& Top()
{
size_t size = _arr.size();
assert(size > 0);
return _arr[0];
}
void Print()
{
for (int i = 0; i < Size(); i++)
{
cout << _arr[i] << " ";
}
cout << endl;
}
protected:
//下調
void _AdjustDown(size_t parent, size_t size)
{
size_t child = 2 * parent + 1;
while (child < size)
{
//child + 1 < size保證是最后一個節點
if (child + 1 < size&&_arr[child] < _arr[child + 1])
{
child++;//孩子節點最大的一個節點
}
//交換
if (_arr[child]>_arr[parent])
{
swap(_arr[child],_arr[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
//上調
void _AdjustUp(int child)
{
int parent = (child - 1) / 2;
int size = _arr.size();
while (child > 0)
{
if (_arr[child] > _arr[parent])
{
swap(_arr[child], _arr[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
protected:
vector<T> _arr;
};test.cpp中
#include<iostream>
using namespace std;
#include"Heap.h"
void Test()
{
int a[] = { 10, 16, 18, 12, 11, 13, 15, 17, 14, 19 };
Heap<int> h(a, sizeof(a) / sizeof(a[0]));
h.Print();
h.push(20);
h.Print();
h.pop();
h.Print();
Heap<int> h2(h);
h2.Print();
}
int main()
{
Test();
system("pause");
return 0;
}免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。