您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹PHP如何實現繪制二叉樹圖形顯示功能,文中介紹的非常詳細,具有一定的參考價值,感興趣的小伙伴們一定要看完!
PHP實現繪制二叉樹圖形顯示功能,具體如下:
前言:
最近老師布置了一個作業:理解并實現平衡二叉樹和紅黑樹,本來老師是說用C#寫的,但是我學的C#基本都還給老師了,怎么辦?那就用現在最熟悉的語言PHP來寫吧!
有一個問題來了,書上在講解樹的時候基本上會給出形象的樹形圖。但是當我們自己試著實現某種樹,在調試、輸出的時候確只能以字符的形式順序地輸出。這給調試等方面帶來了很大的不便。然后在各種百度之后,我發現利用PHP實現二叉樹的圖形顯示的資源幾乎是零!好吧,那我就自己個兒實現一個!
效果顯示:
如果我是直接在這一步擺代碼的話,估計大家會比較煩悶,那我就直接上結果吧,后面在補代碼,先激發激發大家的閱讀興趣:
1、搜索二叉樹:
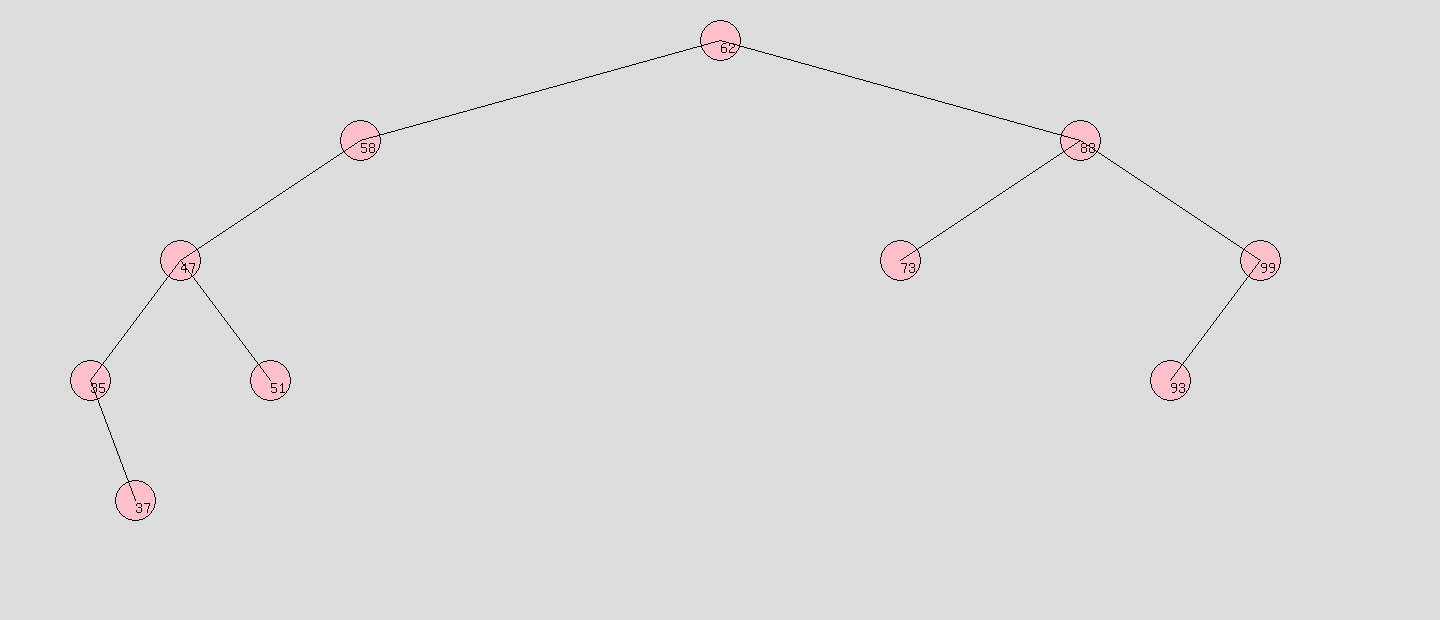
2、平衡二叉樹:
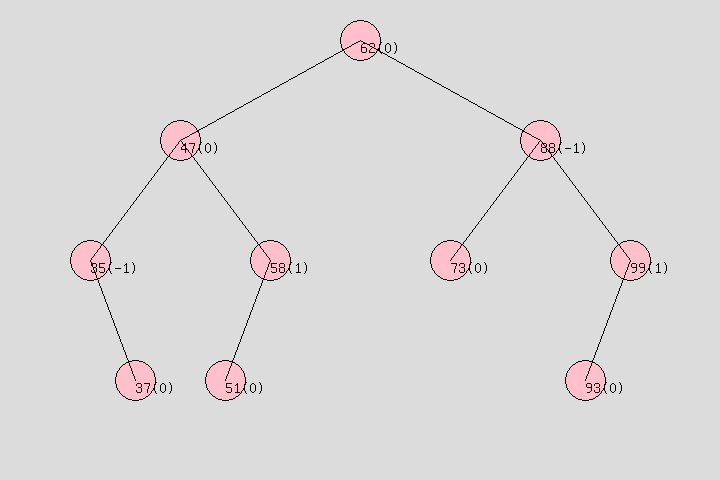
3、紅黑樹:
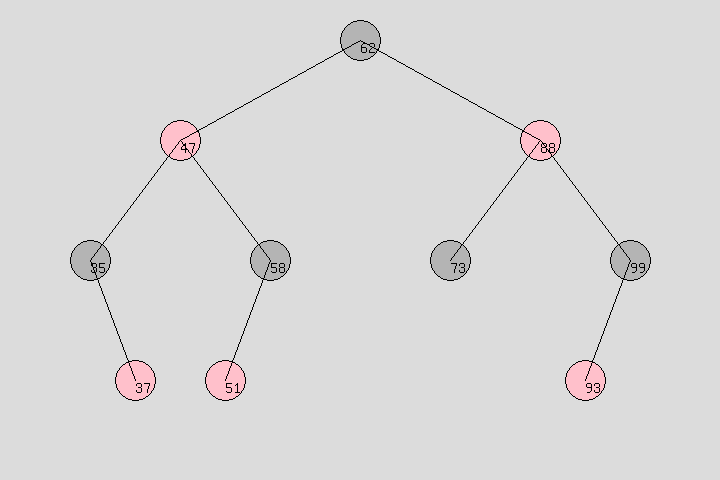
上代碼:
我們給圖片創建一個類吧,顯得稍微的小高級:
image.php 文件:
<?php
/**
* author:LSGOZJ
* description: 繪制二叉樹圖像
*/
class image
{
//樹相關設置
//每層之間的間隔高度
private $level_high = 100;
//最底層葉子結點之間的寬度
private $leaf_width = 50;
//結點圓的半徑
private $rad = 20;
//根節點離邊框頂端距離
private $leave = 20;
//樹(保存樹對象的引用)
private $tree;
//樹的層數
private $level;
//完全二叉樹中最底層葉子結點數量(計算圖像寬度時用到,論如何實現圖片大小自適應)
private $maxCount;
//圖像相關設置
//畫布寬度
private $width;
//畫布高度
private $height;
//畫布背景顏色(RGB)
private $bg = array(
220, 220, 220
);
//節點顏色(搜索二叉樹和平衡二叉樹時用)
private $nodeColor = array(
255, 192, 203
);
//圖像句柄
private $image;
/**
* 構造函數,類屬性初始化
* @param $tree 傳遞一個樹的對象
* @return null
*/
public function __construct($tree)
{
$this->tree = $tree;
$this->level = $this->getLevel();
$this->maxCount = $this->GetMaxCount($this->level);
$this->width = ($this->rad * 2 * $this->maxCount) + $this->maxCount * $this->leaf_width;
$this->height = $this->level * ($this->rad * 2) + $this->level_high * ($this->level - 1) + $this->leave;
//1.創建畫布
$this->image = imagecreatetruecolor($this->width, $this->height); //新建一個真彩色圖像,默認背景是黑色
//填充背景色
$bgcolor = imagecolorallocate($this->image, $this->bg[0], $this->bg[1], $this->bg[2]);
imagefill($this->image, 0, 0, $bgcolor);
}
/**
* 返回傳進來的樹對象對應的完全二叉樹中最底層葉子結點數量
* @param $level 樹的層數
* @return 結點數量
*/
function GetMaxCount($level)
{
return pow(2, $level - 1);
}
/**
* 獲取樹對象的層數
* @param null
* @return 樹的層數
*/
function getLevel()
{
return $this->tree->Depth();
}
/**
* 顯示二叉樹圖像
* @param null
* @return null
*/
public function show()
{
$this->draw($this->tree->root, 1, 0, 0);
header("Content-type:image/png");
imagepng($this->image);
imagedestroy($this->image);
}
/**
* (遞歸)畫出二叉樹的樹狀結構
* @param $root,根節點(樹或子樹) $i,該根節點所處的層 $p_x,父節點的x坐標 $p_y,父節點的y坐標
* @return null
*/
private function draw($root, $i, $p_x, $p_y)
{
if ($i <= $this->level) {
//當前節點的y坐標
$root_y = $i * $this->rad + ($i - 1) * $this->level_high;
//當前節點的x坐標
if (!is_null($parent = $root->parent)) {
if ($root == $parent->left) {
$root_x = $p_x - $this->width / (pow(2, $i));
} else {
$root_x = $p_x + $this->width / (pow(2, $i));
}
} else {
//根節點
$root_x = (1 / 2) * $this->width;
$root_y += $this->leave;
}
//畫結點(確定所畫節點的類型(平衡、紅黑、排序)和方法)
$method = 'draw' . get_class($this->tree) . 'Node';
$this->$method($root_x, $root_y, $root);
//將當前節點和父節點連線(黑色線)
$black = imagecolorallocate($this->image, 0, 0, 0);
if (!is_null($parent = $root->parent)) {
imageline($this->image, $p_x, $p_y, $root_x, $root_y, $black);
}
//畫左子節點
if (!is_null($root->left)) {
$this->draw($root->left, $i + 1, $root_x, $root_y);
}
//畫右子節點
if (!is_null($root->right)) {
$this->draw($root->right, $i + 1, $root_x, $root_y);
}
}
}
/**
* 畫搜索二叉樹結點
* @param $x,當前節點的x坐標 $y,當前節點的y坐標 $node,當前節點的引用
* @return null
*/
private function drawBstNode($x, $y, $node)
{
//節點圓的線顏色
$black = imagecolorallocate($this->image, 0, 0, 0);
$nodeColor = imagecolorallocate($this->image, $this->nodeColor[0], $this->nodeColor[1], $this->nodeColor[2]);
//畫節點圓
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
//節點圓顏色填充
imagefill($this->image, $x, $y, $nodeColor);
//節點對應的數字
imagestring($this->image, 4, $x, $y, $node->key, $black);
}
/**
* 畫平衡二叉樹結點
* @param $x,當前節點的x坐標 $y,當前節點的y坐標 $node,當前節點的引用
* @return null
*/
private function drawAvlNode($x, $y, $node)
{
$black = imagecolorallocate($this->image, 0, 0, 0);
$nodeColor = imagecolorallocate($this->image, $this->nodeColor[0], $this->nodeColor[1], $this->nodeColor[2]);
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
imagefill($this->image, $x, $y, $nodeColor);
imagestring($this->image, 4, $x, $y, $node->key . '(' . $node->bf . ')', $black);
}
/**
* 畫紅黑樹結點
* @param $x,當前節點的x坐標 $y,當前節點的y坐標 $node,當前節點的引用
* @return null
*/
private function drawRbtNode($x, $y, $node)
{
$black = imagecolorallocate($this->image, 0, 0, 0);
$gray = imagecolorallocate($this->image, 180, 180, 180);
$pink = imagecolorallocate($this->image, 255, 192, 203);
imageellipse($this->image, $x, $y, $this->rad * 2, $this->rad * 2, $black);
if ($node->IsRed == TRUE) {
imagefill($this->image, $x, $y, $pink);
} else {
imagefill($this->image, $x, $y, $gray);
}
imagestring($this->image, 4, $x, $y, $node->key, $black);
}
}好,現在我們來看看在客戶端如何調用:
client.php
class Client
{
public static function Main()
{
try {
//實現文件的自動加載
function autoload($class)
{
include strtolower($class) . '.php';
}
spl_autoload_register('autoload');
$arr = array(62, 88, 58, 47, 35, 73, 51, 99, 37, 93);
// $tree = new Bst(); //搜索二叉樹
$tree = new Avl(); //平衡二叉樹
// $tree = new Rbt(); //紅黑樹
$tree->init($arr); //樹的初始化
// $tree->Delete(62);
// $tree->Insert(100);
// $tree->MidOrder(); //樹的中序遍歷(這也是調試的一個手段,看看數字是否從小到大排序)
$image = new image($tree);
$image->show(); //顯示圖像
} catch (Exception $e) {
echo $e->getMessage();
}
}
}
Client::Main();這里用到的那三個樹的類如下:
二叉搜索樹bst.php:
<?php
/**
* author:zhongjin
* description: 二叉查找樹
*/
//結點
class Node
{
public $key;
public $parent;
public $left;
public $right;
public function __construct($key)
{
$this->key = $key;
$this->parent = NULL;
$this->left = NULL;
$this->right = NULL;
}
}
//二叉搜索樹
class Bst
{
public $root;
/**
* 初始化樹結構
* @param $arr 初始化樹結構的數組
* @return null
*/
public function init($arr)
{
$this->root = new Node($arr[0]);
for ($i = 1; $i < count($arr); $i++) {
$this->Insert($arr[$i]);
}
}
/**
* (對內)中序遍歷
* @param $root (樹或子樹的)根節點
* @return null
*/
private function mid_order($root)
{
if ($root != NULL) {
$this->mid_order($root->left);
echo $root->key . " ";
$this->mid_order($root->right);
}
}
/**
* (對外)中序遍歷
* @param null
* @return null
*/
public function MidOrder()
{
$this->mid_order($this->root);
}
/**
* 查找樹中是否存在$key對應的節點
* @param $key 待搜索數字
* @return $key對應的節點
*/
function search($key)
{
$current = $this->root;
while ($current != NULL) {
if ($current->key == $key) {
return $current;
} elseif ($current->key > $key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
return $current;
}
/**
* 查找樹中的最小關鍵字
* @param $root 根節點
* @return 最小關鍵字對應的節點
*/
function search_min($root)
{
$current = $root;
while ($current->left != NULL) {
$current = $current->left;
}
return $current;
}
/**
* 查找樹中的最大關鍵字
* @param $root 根節點
* @return 最大關鍵字對應的節點
*/
function search_max($root)
{
$current = $root;
while ($current->right != NULL) {
$current = $current->right;
}
return $current;
}
/**
* 查找某個$key在中序遍歷時的直接前驅節點
* @param $x 待查找前驅節點的節點引用
* @return 前驅節點引用
*/
function predecessor($x)
{
//左子節點存在,直接返回左子節點的最右子節點
if ($x->left != NULL) {
return $this->search_max($x->left);
}
//否則查找其父節點,直到當前結點位于父節點的右邊
$p = $x->parent;
//如果x是p的左孩子,說明p是x的后繼,我們需要找的是p是x的前驅
while ($p != NULL && $x == $p->left) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 查找某個$key在中序遍歷時的直接后繼節點
* @param $x 待查找后繼節點的節點引用
* @return 后繼節點引用
*/
function successor($x)
{
if ($x->right != NULL) {
return $this->search_min($x->right);
}
$p = $x->parent;
while ($p != NULL && $x == $p->right) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 將$key插入樹中
* @param $key 待插入樹的數字
* @return null
*/
function Insert($key)
{
if (!is_null($this->search($key))) {
throw new Exception('結點' . $key . '已存在,不可插入!');
}
$root = $this->root;
$inode = new Node($key);
$current = $root;
$prenode = NULL;
//為$inode找到合適的插入位置
while ($current != NULL) {
$prenode = $current;
if ($current->key > $inode->key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
$inode->parent = $prenode;
//如果$prenode == NULL, 則證明樹是空樹
if ($prenode == NULL) {
$this->root = $inode;
} else {
if ($inode->key < $prenode->key) {
$prenode->left = $inode;
} else {
$prenode->right = $inode;
}
}
//return $root;
}
/**
* 在樹中刪除$key對應的節點
* @param $key 待刪除節點的數字
* @return null
*/
function Delete($key)
{
if (is_null($this->search($key))) {
throw new Exception('結點' . $key . "不存在,刪除失敗!");
}
$root = $this->root;
$dnode = $this->search($key);
if ($dnode->left == NULL || $dnode->right == NULL) { #如果待刪除結點無子節點或只有一個子節點,則c = dnode
$c = $dnode;
} else { #如果待刪除結點有兩個子節點,c置為dnode的直接后繼,以待最后將待刪除結點的值換為其后繼的值
$c = $this->successor($dnode);
}
//無論前面情況如何,到最后c只剩下一邊子結點
if ($c->left != NULL) {
$s = $c->left;
} else {
$s = $c->right;
}
if ($s != NULL) { #將c的子節點的父母結點置為c的父母結點,此處c只可能有1個子節點,因為如果c有兩個子節點,則c不可能是dnode的直接后繼
$s->parent = $c->parent;
}
if ($c->parent == NULL) { #如果c的父母為空,說明c=dnode是根節點,刪除根節點后直接將根節點置為根節點的子節點,此處dnode是根節點,且擁有兩個子節點,則c是dnode的后繼結點,c的父母就不會為空,就不會進入這個if
$this->root = $s;
} else if ($c == $c->parent->left) { #如果c是其父節點的左右子節點,則將c父母的左右子節點置為c的左右子節點
$c->parent->left = $s;
} else {
$c->parent->right = $s;
}
#如果c!=dnode,說明c是dnode的后繼結點,交換c和dnode的key值
if ($c != $dnode) {
$dnode->key = $c->key;
}
#返回根節點
// return $root;
}
/**
* (對內)獲取樹的深度
* @param $root 根節點
* @return 樹的深度
*/
private function getdepth($root)
{
if ($root == NULL) {
return 0;
}
$dl = $this->getdepth($root->left);
$dr = $this->getdepth($root->right);
return ($dl > $dr ? $dl : $dr) + 1;
}
/**
* (對外)獲取樹的深度
* @param null
* @return null
*/
public function Depth()
{
return $this->getdepth($this->root);
}
}
?>平衡二叉樹avl.php:
<?php
/**
* author:zhongjin
* description: 平衡二叉樹
*/
//結點
class Node
{
public $key;
public $parent;
public $left;
public $right;
public $bf; //平衡因子
public function __construct($key)
{
$this->key = $key;
$this->parent = NULL;
$this->left = NULL;
$this->right = NULL;
$this->bf = 0;
}
}
//平衡二叉樹
class Avl
{
public $root;
const LH = +1; //左高
const EH = 0; //等高
const RH = -1; //右高
/**
* 初始化樹結構
* @param $arr 初始化樹結構的數組
* @return null
*/
public function init($arr)
{
$this->root = new Node($arr[0]);
for ($i = 1; $i < count($arr); $i++) {
$this->Insert($arr[$i]);
}
}
/**
* (對內)中序遍歷
* @param $root (樹或子樹的)根節點
* @return null
*/
private function mid_order($root)
{
if ($root != NULL) {
$this->mid_order($root->left);
echo $root->key . "-" . $root->bf . " ";
$this->mid_order($root->right);
}
}
/**
* (對外)中序遍歷
* @param null
* @return null
*/
public function MidOrder()
{
$this->mid_order($this->root);
}
/**
* 將以$root為根節點的最小不平衡二叉樹做右旋處理
* @param $root(樹或子樹)根節點
* @return null
*/
private function R_Rotate($root)
{
$L = $root->left;
if (!is_NULL($root->parent)) {
$P = $root->parent;
if ($root == $P->left) {
$P->left = $L;
} else {
$P->right = $L;
}
$L->parent = $P;
} else {
$L->parent = NULL;
}
$root->parent = $L;
$root->left = $L->right;
$L->right = $root;
//這句必須啊!
if ($L->parent == NULL) {
$this->root = $L;
}
}
/**
* 將以$root為根節點的最小不平衡二叉樹做左旋處理
* @param $root(樹或子樹)根節點
* @return null
*/
private function L_Rotate($root)
{
$R = $root->right;
if (!is_NULL($root->parent)) {
$P = $root->parent;
if ($root == $P->left) {
$P->left = $R;
} else {
$P->right = $R;
}
$R->parent = $P;
} else {
$R->parent = NULL;
}
$root->parent = $R;
$root->right = $R->left;
$R->left = $root;
//這句必須啊!
if ($R->parent == NULL) {
$this->root = $R;
}
}
/**
* 對以$root所指結點為根節點的二叉樹作左平衡處理
* @param $root(樹或子樹)根節點
* @return null
*/
public function LeftBalance($root)
{
$L = $root->left;
$L_bf = $L->bf;
switch ($L_bf) {
//檢查root的左子樹的平衡度,并作相應的平衡處理
case self::LH: //新結點插入在root的左孩子的左子樹上,要做單右旋處理
$root->bf = $L->bf = self::EH;
$this->R_Rotate($root);
break;
case self::RH: //新節點插入在root的左孩子的右子樹上,要做雙旋處理
$L_r = $L->right; //root左孩子的右子樹根
$L_r_bf = $L_r->bf;
//修改root及其左孩子的平衡因子
switch ($L_r_bf) {
case self::LH:
$root->bf = self::RH;
$L->bf = self::EH;
break;
case self::EH:
$root->bf = $L->bf = self::EH;
break;
case self::RH:
$root->bf = self::EH;
$L->bf = self::LH;
break;
}
$L_r->bf = self::EH;
//對root的左子樹作左平衡處理
$this->L_Rotate($L);
//對root作右平衡處理
$this->R_Rotate($root);
}
}
/**
* 對以$root所指結點為根節點的二叉樹作右平衡處理
* @param $root(樹或子樹)根節點
* @return null
*/
public function RightBalance($root)
{
$R = $root->right;
$R_bf = $R->bf;
switch ($R_bf) {
//檢查root的右子樹的平衡度,并作相應的平衡處理
case self::RH: //新結點插入在root的右孩子的右子樹上,要做單左旋處理
$root->bf = $R->bf = self::EH;
$this->L_Rotate($root);
break;
case self::LH: //新節點插入在root的右孩子的左子樹上,要做雙旋處理
$R_l = $R->left; //root右孩子的左子樹根
$R_l_bf = $R_l->bf;
//修改root及其右孩子的平衡因子
switch ($R_l_bf) {
case self::RH:
$root->bf = self::LH;
$R->bf = self::EH;
break;
case self::EH:
$root->bf = $R->bf = self::EH;
break;
case self::LH:
$root->bf = self::EH;
$R->bf = self::RH;
break;
}
$R_l->bf = self::EH;
//對root的右子樹作右平衡處理
$this->R_Rotate($R);
//對root作左平衡處理
$this->L_Rotate($root);
}
}
/**
* 查找樹中是否存在$key對應的節點
* @param $key 待搜索數字
* @return $key對應的節點
*/
public function search($key)
{
$current = $this->root;
while ($current != NULL) {
if ($current->key == $key) {
return $current;
} elseif ($current->key > $key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
return $current;
}
/**
* 查找樹中的最小關鍵字
* @param $root 根節點
* @return 最小關鍵字對應的節點
*/
function search_min($root)
{
$current = $root;
while ($current->left != NULL) {
$current = $current->left;
}
return $current;
}
/**
* 查找樹中的最大關鍵字
* @param $root 根節點
* @return 最大關鍵字對應的節點
*/
function search_max($root)
{
$current = $root;
while ($current->right != NULL) {
$current = $current->right;
}
return $current;
}
/**
* 查找某個$key在中序遍歷時的直接前驅節點
* @param $x 待查找前驅節點的節點引用
* @return 前驅節點引用
*/
private function predecessor($x)
{
//左子節點存在,直接返回左子節點的最右子節點
if ($x->left != NULL) {
return $this->search_max($x->left);
}
//否則查找其父節點,直到當前結點位于父節點的右邊
$p = $x->parent;
//如果x是p的左孩子,說明p是x的后繼,我們需要找的是p是x的前驅
while ($p != NULL && $x == $p->left) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 查找某個$key在中序遍歷時的直接后繼節點
* @param $x 待查找后繼節點的節點引用
* @return 后繼節點引用
*/
private function successor($x)
{
if ($x->left != NULL) {
return $this->search_min($x->right);
}
$p = $x->parent;
while ($p != NULL && $x == $p->right) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* (對內)插入結點,如果結點不存在則插入,失去平衡要做平衡處理
* @param $root 根節點 $key 待插入樹的數字
* @return null
*/
private function insert_node(&$root, $key)
{
//找到了插入的位置,插入新節點
if (is_null($root)) {
$root = new Node($key);
//插入結點成功
return TRUE;
} else {
//在樹中已經存在和$key相等的結點
if ($key == $root->key) {
//插入節點失敗
return FALSE;
} //在root的左子樹中繼續搜索
elseif ($key < $root->key) {
//插入左子樹失敗
if (!($this->insert_node($root->left, $key))) {
//樹未長高
return FALSE;
}
//成功插入,修改平衡因子
if (is_null($root->left->parent)) {
$root->left->parent = $root;
}
switch ($root->bf) {
//原來左右子樹等高,現在左子樹增高而樹增高
case self::EH:
$root->bf = self::LH;
//樹長高
return TRUE;
break;
//原來左子樹比右子樹高,需要做左平衡處理
case self::LH:
$this->LeftBalance($root);
//平衡后,樹并未長高
return FALSE;
break;
//原來右子樹比左子樹高,現在左右子樹等高
case self::RH:
$root->bf = self::EH;
//樹并未長高
return FALSE;
break;
}
} //在root的右子樹中繼續搜索
else {
//插入右子樹失敗
if (!$this->insert_node($root->right, $key)) {
//樹未長高
return FALSE;
}
//成功插入,修改平衡因子
if (is_null($root->right->parent)) {
$root->right->parent = $root;
}
switch ($root->bf) {
//原來左右子樹等高,現在右子樹增高而樹增高
case self::EH:
$root->bf = self::RH;
//樹長高
return TRUE;
break;
//原來左子樹比右子樹高,現在左右子樹等高
case self::LH:
$root->bf = self::EH;
return FALSE;
break;
//原來右子樹比左子樹高,要做右平衡處理
case self::RH:
$this->RightBalance($root);
//樹并未長高
return FALSE;
break;
}
}
}
}
/**
* (對外)將$key插入樹中
* @param $key 待插入樹的數字
* @return null
*/
public function Insert($key)
{
$this->insert_node($this->root, $key);
}
/**
* 獲取待刪除的節點(刪除的最終節點)
* @param $key 待刪除的數字
* @return 最終被刪除的節點
*/
private function get_del_node($key)
{
$dnode = $this->search($key);
if ($dnode == NULL) {
throw new Exception("結點不存在!");
return;
}
if ($dnode->left == NULL || $dnode->right == NULL) { #如果待刪除結點無子節點或只有一個子節點,則c = dnode
$c = $dnode;
} else { #如果待刪除結點有兩個子節點,c置為dnode的直接后繼,以待最后將待刪除結點的值換為其后繼的值
$c = $this->successor($dnode);
}
$dnode->key = $c->key;
return $c;
}
/**
* (對內)刪除指定節點,處理該結點往上結點的平衡因子
* @param $node 最終該被刪除的節點
* @return null
*/
private function del_node($node)
{
if ($node == $this->root) {
$this->root = NULL;
return;
}
$current = $node;
//現在的node只有兩種情況,要么只有一個子節點,要么沒有子節點
$P = $current->parent;
//刪除一個結點,第一個父節點的平衡都肯定會發生變化
$lower = TRUE;
while ($lower == TRUE && !is_null($P)) {
//待刪除結點是左節點
if ($current == $P->left) {
if($current == $node){
if (!is_null($current->left)) {
$P->left = $current->left;
} else {
$P->left = $current->left;
}
}
$P_bf = $P->bf;
switch ($P_bf) {
case self::LH:
$P->bf = self::EH;
$lower = TRUE;
$current = $P;
$P = $current->parent;
break;
case self::EH:
$P->bf = self::RH;
$lower = FALSE;
break;
case self::RH:
$this->RightBalance($P);
$lower = TRUE;
$current = $P->parent;
$P = $current->parent;
break;
}
} //右結點
else {
if($current == $node){
if (!is_null($current->left)) {
$P->right = $current->left;
} else {
$P->right = $current->left;
}
}
$P_bf = $P->bf;
switch ($P_bf) {
case self::LH:
$this->LeftBalance($P);
$lower = TRUE;
$current = $P->parent;
$P = $current->parent;
break;
case self::EH:
$P->bf = self::LH;
$lower = FALSE;
break;
case self::RH:
$P->bf = self::LH;
$lower = TRUE;
$current = $P;
$P = $current->parent;
break;
}
}
}
}
/**
* (對外)刪除指定節點
* @param $key 刪除節點的key值
* @return null
*/
public function Delete($key)
{
$del_node = $this->get_del_node($key);
$this->del_node($del_node);
}
/**
* (對內)獲取樹的深度
* @param $root 根節點
* @return 樹的深度
*/
private function getdepth($root)
{
if ($root == NULL) {
return 0;
}
$dl = $this->getdepth($root->left);
$dr = $this->getdepth($root->right);
return ($dl > $dr ? $dl : $dr) + 1;
}
/**
* (對外)獲取樹的深度
* @param null
* @return null
*/
public function Depth()
{
return $this->getdepth($this->root);
}
}
?>紅黑樹rbt.php:
<?php
/**
* author:zhongjin
* description: 紅黑樹
*/
//結點
class Node
{
public $key;
public $parent;
public $left;
public $right;
public $IsRed; //分辨紅節點或黑節點
public function __construct($key, $IsRed = TRUE)
{
$this->key = $key;
$this->parent = NULL;
$this->left = NULL;
$this->right = NULL;
//插入結點默認是紅色
$this->IsRed = $IsRed;
}
}
//紅黑樹
class Rbt
{
public $root;
/**
* 初始化樹結構
* @param $arr 初始化樹結構的數組
* @return null
*/
public function init($arr)
{
//根節點必須是黑色
$this->root = new Node($arr[0], FALSE);
for ($i = 1; $i < count($arr); $i++) {
$this->Insert($arr[$i]);
}
}
/**
* (對內)中序遍歷
* @param $root (樹或子樹的)根節點
* @return null
*/
private function mid_order($root)
{
if ($root != NULL) {
$this->mid_order($root->left);
echo $root->key . "-" . ($root->IsRed ? 'r' : 'b') . ' ';
$this->mid_order($root->right);
}
}
/**
* (對外)中序遍歷
* @param null
* @return null
*/
public function MidOrder()
{
$this->mid_order($this->root);
}
/**
* 查找樹中是否存在$key對應的節點
* @param $key 待搜索數字
* @return $key對應的節點
*/
function search($key)
{
$current = $this->root;
while ($current != NULL) {
if ($current->key == $key) {
return $current;
} elseif ($current->key > $key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
//結點不存在
return $current;
}
/**
* 將以$root為根節點的最小不平衡二叉樹做右旋處理
* @param $root(樹或子樹)根節點
* @return null
*/
private function R_Rotate($root)
{
$L = $root->left;
if (!is_null($root->parent)) {
$P = $root->parent;
if($root == $P->left){
$P->left = $L;
}else{
$P->right = $L;
}
$L->parent = $P;
} else {
$L->parent = NULL;
}
$root->parent = $L;
$root->left = $L->right;
$L->right = $root;
//這句必須啊!
if ($L->parent == NULL) {
$this->root = $L;
}
}
/**
* 將以$root為根節點的最小不平衡二叉樹做左旋處理
* @param $root(樹或子樹)根節點
* @return null
*/
private function L_Rotate($root)
{
$R = $root->right;
if (!is_null($root->parent)) {
$P = $root->parent;
if($root == $P->right){
$P->right = $R;
}else{
$P->left = $R;
}
$R->parent = $P;
} else {
$R->parent = NULL;
}
$root->parent = $R;
$root->right = $R->left;
$R->left = $root;
//這句必須啊!
if ($R->parent == NULL) {
$this->root = $R;
}
}
/**
* 查找樹中的最小關鍵字
* @param $root 根節點
* @return 最小關鍵字對應的節點
*/
function search_min($root)
{
$current = $root;
while ($current->left != NULL) {
$current = $current->left;
}
return $current;
}
/**
* 查找樹中的最大關鍵字
* @param $root 根節點
* @return 最大關鍵字對應的節點
*/
function search_max($root)
{
$current = $root;
while ($current->right != NULL) {
$current = $current->right;
}
return $current;
}
/**
* 查找某個$key在中序遍歷時的直接前驅節點
* @param $x 待查找前驅節點的節點引用
* @return 前驅節點引用
*/
function predecessor($x)
{
//左子節點存在,直接返回左子節點的最右子節點
if ($x->left != NULL) {
return $this->search_max($x->left);
}
//否則查找其父節點,直到當前結點位于父節點的右邊
$p = $x->parent;
//如果x是p的左孩子,說明p是x的后繼,我們需要找的是p是x的前驅
while ($p != NULL && $x == $p->left) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 查找某個$key在中序遍歷時的直接后繼節點
* @param $x 待查找后繼節點的節點引用
* @return 后繼節點引用
*/
function successor($x)
{
if ($x->left != NULL) {
return $this->search_min($x->right);
}
$p = $x->parent;
while ($p != NULL && $x == $p->right) {
$x = $p;
$p = $p->parent;
}
return $p;
}
/**
* 將$key插入樹中
* @param $key 待插入樹的數字
* @return null
*/
public function Insert($key)
{
if (!is_null($this->search($key))) {
throw new Exception('結點' . $key . '已存在,不可插入!');
}
$root = $this->root;
$inode = new Node($key);
$current = $root;
$prenode = NULL;
//為$inode找到合適的插入位置
while ($current != NULL) {
$prenode = $current;
if ($current->key > $inode->key) {
$current = $current->left;
} else {
$current = $current->right;
}
}
$inode->parent = $prenode;
//如果$prenode == NULL, 則證明樹是空樹
if ($prenode == NULL) {
$this->root = $inode;
} else {
if ($inode->key < $prenode->key) {
$prenode->left = $inode;
} else {
$prenode->right = $inode;
}
}
//將它重新修正為一顆紅黑樹
$this->InsertFixUp($inode);
}
/**
* 對插入節點的位置及往上的位置進行顏色調整
* @param $inode 插入的節點
* @return null
*/
private function InsertFixUp($inode)
{
//情況一:需要調整條件,父節點存在且父節點的顏色是紅色
while (($parent = $inode->parent) != NULL && $parent->IsRed == TRUE) {
//祖父結點:
$gparent = $parent->parent;
//如果父節點是祖父結點的左子結點,下面的else與此相反
if ($parent == $gparent->left) {
//叔叔結點
$uncle = $gparent->right;
//case1:叔叔結點也是紅色
if ($uncle != NULL && $uncle->IsRed == TRUE) {
//將父節點和叔叔結點都涂黑,將祖父結點涂紅
$parent->IsRed = FALSE;
$uncle->IsRed = FALSE;
$gparent->IsRed = TRUE;
//將新節點指向祖父節點(現在祖父結點變紅,可以看作新節點存在)
$inode = $gparent;
//繼續while循環,重新判斷
continue; //經過這一步之后,組父節點作為新節點存在(跳到case2)
}
//case2:叔叔結點是黑色,且當前結點是右子節點
if ($inode == $parent->right) {
//以父節點作為旋轉結點做左旋轉處理
$this->L_Rotate($parent);
//在樹中實際上已經轉換,但是這里的變量的指向還沒交換,
//將父節點和字節調換一下,為下面右旋做準備
$temp = $parent;
$parent = $inode;
$inode = $temp;
}
//case3:叔叔結點是黑色,而且當前結點是父節點的左子節點
$parent->IsRed = FALSE;
$gparent->IsRed = TRUE;
$this->R_Rotate($gparent);
} //如果父節點是祖父結點的右子結點,與上面完全相反
else {
//叔叔結點
$uncle = $gparent->left;
//case1:叔叔結點也是紅色
if ($uncle != NULL && $uncle->IsRed == TRUE) {
//將父節點和叔叔結點都涂黑,將祖父結點涂紅
$parent->IsRed = FALSE;
$uncle->IsRed = FALSE;
$gparent->IsRed = TRUE;
//將新節點指向祖父節點(現在祖父結點變紅,可以看作新節點存在)
$inode = $gparent;
//繼續while循環,重新判斷
continue; //經過這一步之后,組父節點作為新節點存在(跳到case2)
}
//case2:叔叔結點是黑色,且當前結點是左子節點
if ($inode == $parent->left) {
//以父節點作為旋轉結點做右旋轉處理
$this->R_Rotate($parent);
//在樹中實際上已經轉換,但是這里的變量的指向還沒交換,
//將父節點和字節調換一下,為下面右旋做準備
$temp = $parent;
$parent = $inode;
$inode = $temp;
}
//case3:叔叔結點是黑色,而且當前結點是父節點的右子節點
$parent->IsRed = FALSE;
$gparent->IsRed = TRUE;
$this->L_Rotate($gparent);
}
}
//情況二:原樹是根節點(父節點為空),則只需將根節點涂黑
if ($inode == $this->root) {
$this->root->IsRed = FALSE;
return;
}
//情況三:插入節點的父節點是黑色,則什么也不用做
if ($inode->parent != NULL && $inode->parent->IsRed == FALSE) {
return;
}
}
/**
* (對外)刪除指定節點
* @param $key 刪除節點的key值
* @return null
*/
function Delete($key)
{
if (is_null($this->search($key))) {
throw new Exception('結點' . $key . "不存在,刪除失敗!");
}
$dnode = $this->search($key);
if ($dnode->left == NULL || $dnode->right == NULL) { #如果待刪除結點無子節點或只有一個子節點,則c = dnode
$c = $dnode;
} else { #如果待刪除結點有兩個子節點,c置為dnode的直接后繼,以待最后將待刪除結點的值換為其后繼的值
$c = $this->successor($dnode);
}
//為了后面顏色處理做準備
$parent = $c->parent;
//無論前面情況如何,到最后c只剩下一邊子結點
if ($c->left != NULL) { //這里不會出現,除非選擇的是刪除結點的前驅
$s = $c->left;
} else {
$s = $c->right;
}
if ($s != NULL) { #將c的子節點的父母結點置為c的父母結點,此處c只可能有1個子節點,因為如果c有兩個子節點,則c不可能是dnode的直接后繼
$s->parent = $c->parent;
}
if ($c->parent == NULL) { #如果c的父母為空,說明c=dnode是根節點,刪除根節點后直接將根節點置為根節點的子節點,此處dnode是根節點,且擁有兩個子節點,則c是dnode的后繼結點,c的父母就不會為空,就不會進入這個if
$this->root = $s;
} else if ($c == $c->parent->left) { #如果c是其父節點的左右子節點,則將c父母的左右子節點置為c的左右子節點
$c->parent->left = $s;
} else {
$c->parent->right = $s;
}
$dnode->key = $c->key;
$node = $s;
//c的結點顏色是黑色,那么會影響路徑上的黑色結點的數量,必須進行調整
if ($c->IsRed == FALSE) {
$this->DeleteFixUp($node,$parent);
}
}
/**
* 刪除節點后對接點周圍的其他節點進行調整
* @param $key 刪除節點的子節點和父節點
* @return null
*/
private function DeleteFixUp($node,$parent)
{
//如果待刪結點的子節點為紅色,直接將子節點涂黑
if ($node != NULL && $node->IsRed == TRUE) {
$node->IsRed = FALSE;
return;
}
//如果是根節點,那就直接將根節點置為黑色即可
while (($node == NULL || $node->IsRed == FALSE) && ($node != $this->root)) {
//node是父節點的左子節點,下面else與這里相反
if ($node == $parent->left) {
$brother = $parent->right;
//case1:兄弟結點顏色是紅色(父節點和兄弟孩子結點都是黑色)
//將父節點涂紅,將兄弟結點涂黑,然后對父節點進行左旋處理(經過這一步,情況轉換為兄弟結點顏色為黑色的情況)
if ($brother->IsRed == TRUE) {
$brother->IsRed = FALSE;
$parent->IsRed = TRUE;
$this->L_Rotate($parent);
//將情況轉化為其他的情況
$brother = $parent->right; //在左旋處理后,$parent->right指向的是原來兄弟結點的左子節點
}
//以下是兄弟結點為黑色的情況
//case2:兄弟結點是黑色,且兄弟結點的兩個子節點都是黑色
//將兄弟結點涂紅,將當前結點指向其父節點,將其父節點指向當前結點的祖父結點。
if (($brother->left == NULL || $brother->left->IsRed == FALSE) && ($brother->right == NULL || $brother->right->IsRed == FALSE)) {
$brother->IsRed = TRUE;
$node = $parent;
$parent = $node->parent;
} else {
//case3:兄弟結點是黑色,兄弟結點的左子節點是紅色,右子節點為黑色
//將兄弟結點涂紅,將兄弟節點的左子節點涂黑,然后對兄弟結點做右旋處理(經過這一步,情況轉換為兄弟結點顏色為黑色,右子節點為紅色的情況)
if ($brother->right == NULL || $brother->right->IsRed == FALSE) {
$brother->IsRed = TRUE;
$brother->left->IsRed = FALSE;
$this->R_Rotate($brother);
//將情況轉換為其他情況
$brother = $parent->right;
}
//case4:兄弟結點是黑色,且兄弟結點的右子節點為紅色,左子節點為任意顏色
//將兄弟節點涂成父節點的顏色,再把父節點涂黑,將兄弟結點的右子節點涂黑,然后對父節點做左旋處理
$brother->IsRed = $parent->IsRed;
$parent->IsRed = FALSE;
$brother->right->IsRed = FALSE;
$this->L_Rotate($parent);
//到了第四種情況,已經是最基本的情況了,可以直接退出了
$node = $this->root;
break;
}
} //node是父節點的右子節點
else {
$brother = $parent->left;
//case1:兄弟結點顏色是紅色(父節點和兄弟孩子結點都是黑色)
//將父節點涂紅,將兄弟結點涂黑,然后對父節點進行右旋處理(經過這一步,情況轉換為兄弟結點顏色為黑色的情況)
if ($brother->IsRed == TRUE) {
$brother->IsRed = FALSE;
$parent->IsRed = TRUE;
$this->R_Rotate($parent);
//將情況轉化為其他的情況
$brother = $parent->left; //在右旋處理后,$parent->left指向的是原來兄弟結點的右子節點
}
//以下是兄弟結點為黑色的情況
//case2:兄弟結點是黑色,且兄弟結點的兩個子節點都是黑色
//將兄弟結點涂紅,將當前結點指向其父節點,將其父節點指向當前結點的祖父結點。
if (($brother->left == NULL || $brother->left->IsRed == FALSE) && ($brother->right == NULL || $brother->right->IsRed == FALSE)) {
$brother->IsRed = TRUE;
$node = $parent;
$parent = $node->parent;
} else {
//case3:兄弟結點是黑色,兄弟結點的右子節點是紅色,左子節點為黑色
//將兄弟結點涂紅,將兄弟節點的左子節點涂黑,然后對兄弟結點做左旋處理(經過這一步,情況轉換為兄弟結點顏色為黑色,右子節點為紅色的情況)
if ($brother->left == NULL || $brother->left->IsRed == FALSE) {
$brother->IsRed = TRUE;
$brother->right = FALSE;
$this->L_Rotate($brother);
//將情況轉換為其他情況
$brother = $parent->left;
}
//case4:兄弟結點是黑色,且兄弟結點的左子節點為紅色,右子節點為任意顏色
//將兄弟節點涂成父節點的顏色,再把父節點涂黑,將兄弟結點的右子節點涂黑,然后對父節點左左旋處理
$brother->IsRed = $parent->IsRed;
$parent->IsRed = FALSE;
$brother->left->IsRed = FALSE;
$this->R_Rotate($parent);
$node = $this->root;
break;
}
}
}
if ($node != NULL) {
$this->root->IsRed = FALSE;
}
}
/**
* (對內)獲取樹的深度
* @param $root 根節點
* @return 樹的深度
*/
private function getdepth($root)
{
if ($root == NULL) {
return 0;
}
$dl = $this->getdepth($root->left);
$dr = $this->getdepth($root->right);
return ($dl > $dr ? $dl : $dr) + 1;
}
/**
* (對外)獲取樹的深度
* @param null
* @return null
*/
public function Depth()
{
return $this->getdepth($this->root);
}
}
?>php,一個嵌套的縮寫名稱,是英文超級文本預處理語言(PHP:Hypertext Preprocessor)的縮寫。PHP 是一種 HTML 內嵌式的語言,PHP與微軟的ASP頗有幾分相似,都是一種在服務器端執行的嵌入HTML文檔的腳本語言,語言的風格有類似于C語言,現在被很多的網站編程人員廣泛的運用。
以上是“PHP如何實現繪制二叉樹圖形顯示功能”這篇文章的所有內容,感謝各位的閱讀!希望分享的內容對大家有幫助,更多相關知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。