Python進行數據相關性分析的三種方式是什么

本文小編為大家詳細介紹“Python進行數據相關性分析的三種方式是什么”，內容詳細，步驟清晰，細節處理妥當，希望這篇“Python進行數據相關性分析的三種方式是什么”文章能幫助大家解決疑惑，下面跟著小編的思路慢慢深入，一起來學習新知識吧。

相關性實現

統計和數據科學通常關注數據集的兩個或多個變量（或特征）之間的關系。數據集中的每個數據點都是一個觀察值，特征是這些觀察值的屬性或屬性。

這里主要介紹下面3種相關性的計算方式：

• Pearson’s r

• Spearman’s rho

• Kendall’s tau

NumPy 相關性計算

np.corrcoef() 返回 Pearson 相關系數矩陣。

import numpy as np
x = np.arange(10, 20)
x
array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])

y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
y
array([ 2,  1,  4,  5,  8, 12, 18, 25, 96, 48])

r = np.corrcoef(x, y)
r
array([[1.        , 0.75864029],
       [0.75864029, 1.        ]])

SciPy 相關性計算

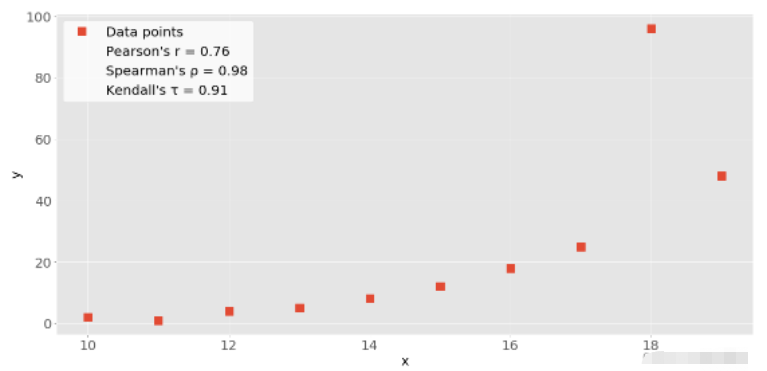
import numpy as np
import scipy.stats
x = np.arange(10, 20)
y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])

scipy.stats.pearsonr(x, y)    # Pearson's r
(0.7586402890911869, 0.010964341301680832)

scipy.stats.spearmanr(x, y)   # Spearman's rho
SpearmanrResult(correlation=0.9757575757575757, pvalue=1.4675461874042197e-06)

scipy.stats.kendalltau(x, y)  # Kendall's tau
KendalltauResult(correlation=0.911111111111111, pvalue=2.9761904761904762e-05)

在檢驗假設時，您可以在統計方法中使用p 值。p 值是一項重要的衡量標準，需要深入了解概率和統計數據才能進行解釋。

scipy.stats.pearsonr(x, y)[0]    # Pearson's r
0.7586402890911869
scipy.stats.spearmanr(x, y)[0]   # Spearman's rho
0.9757575757575757
scipy.stats.kendalltau(x, y)[0]  # Kendall's tau
0.911111111111111

Pandas 相關性計算

相對于來說計算比較簡單。

import pandas as pd
x = pd.Series(range(10, 20))
y = pd.Series([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])

x.corr(y)                     # Pearson's r
0.7586402890911867
y.corr(x)
0.7586402890911869
x.corr(y, method='spearman')  # Spearman's rho
0.9757575757575757
x.corr(y, method='kendall')   # Kendall's tau
0.911111111111111

線性相關實現

線性相關性測量變量或數據集特征之間的數學關系與線性函數的接近程度。如果兩個特征之間的關系更接近某個線性函數，那么它們的線性相關性更強，相關系數的絕對值也更高。

線性回歸：SciPy 實現

線性回歸是尋找盡可能接近特征之間實際關系的線性函數的過程。換句話說，您確定最能描述特征之間關聯的線性函數，這種線性函數也稱為回歸線。

import pandas as pd
x = pd.Series(range(10, 20))
y = pd.Series([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])

使用scipy.stats.linregress()對兩個長度相同的數組執行線性回歸。

result = scipy.stats.linregress(x, y)
scipy.stats.linregress(xy)
LinregressResult(slope=7.4363636363636365, intercept=-85.92727272727274, rvalue=0.7586402890911869, pvalue=0.010964341301680825, stderr=2.257878767543913)

result.slope # 回歸線的斜率
7.4363636363636365

result.intercept # 回歸線的截距
-85.92727272727274

result.rvalue # 相關系數
0.7586402890911869

result.pvalue #  p值
0.010964341301680825

result.stderr # 估計梯度的標準誤差
2.257878767543913

未來更多內容參考機器學習專欄中的線性回歸內容。

等級相關

比較與兩個變量或數據集特征相關的數據的排名或排序。如果排序相似則相關性強、正且高。但是如果順序接近反轉，則相關性為強、負和低。換句話說等級相關性僅與值的順序有關，而不與數據集中的特定值有關。

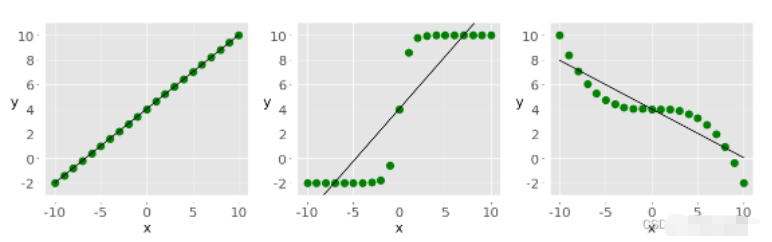
圖1和圖2顯示了較大的 x 值始終對應于較大的 y 值的觀察結果，這是完美的正等級相關。圖3說明了相反的情況即完美的負等級相關。

排名：SciPy 實現

使用 scipy.stats.rankdata() 來確定數組中每個值的排名。

import numpy as np
import scipy.stats
x = np.arange(10, 20)
y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])

# 獲取排名序
scipy.stats.rankdata(x)  # 單調遞增
array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])
scipy.stats.rankdata(y)
array([ 2.,  1.,  3.,  4.,  5.,  6.,  7.,  8., 10.,  9.])
scipy.stats.rankdata(z) # 單調遞減
array([10.,  9.,  8.,  7.,  6.,  5.,  4.,  3.,  2.,  1.])

rankdata() 將nan值視為極大。

scipy.stats.rankdata([8, np.nan, 0, 2])
array([3., 4., 1., 2.])

等級相關性：NumPy 和 SciPy 實現

使用 scipy.stats.spearmanr() 計算 Spearman 相關系數。

result = scipy.stats.spearmanr(x, y)
result
SpearmanrResult(correlation=0.9757575757575757, pvalue=1.4675461874042197e-06)

result.correlation
0.9757575757575757

result.pvalue
1.4675461874042197e-06

rho, p = scipy.stats.spearmanr(x, y)
rho
0.9757575757575757

p
1.4675461874042197e-06

等級相關性：Pandas 實現

使用 Pandas 計算 Spearman 和 Kendall 相關系數。

import numpy as np
import scipy.stats
x = np.arange(10, 20)
y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])

x, y, z = pd.Series(x), pd.Series(y), pd.Series(z)
xy = pd.DataFrame({'x-values': x, 'y-values': y})
xyz = pd.DataFrame({'x-values': x, 'y-values': y, 'z-values': z})

計算 Spearman 的 rho，method=spearman。

x.corr(y, method='spearman')
0.9757575757575757

xy.corr(method='spearman')
          x-values  y-values
x-values  1.000000  0.975758
y-values  0.975758  1.000000

xyz.corr(method='spearman')
          x-values  y-values  z-values
x-values  1.000000  0.975758 -1.000000
y-values  0.975758  1.000000 -0.975758
z-values -1.000000 -0.975758  1.000000

xy.corrwith(z, method='spearman')
x-values   -1.000000
y-values   -0.975758
dtype: float64

計算 Kendall 的 tau， method=kendall。

x.corr(y, method='kendall')
0.911111111111111

xy.corr(method='kendall')
          x-values  y-values
x-values  1.000000  0.911111
y-values  0.911111  1.000000

xyz.corr(method='kendall')
          x-values  y-values  z-values
x-values  1.000000  0.911111 -1.000000
y-values  0.911111  1.000000 -0.911111
z-values -1.000000 -0.911111  1.000000

xy.corrwith(z, method='kendall')
x-values   -1.000000
y-values   -0.911111
dtype: float64

相關性的可視化

數據可視化在統計學和數據科學中非常重要。可以幫助更好地理解的數據，并更好地了解特征之間的關系。

這里使用 matplotlib 來進行數據可視化。

import matplotlib.pyplot as plt
plt.style.use('ggplot')

import numpy as np
import scipy.stats
x = np.arange(10, 20)
y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
                [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
                [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])

帶有回歸線的 XY 圖

使用 linregress() 獲得回歸線的斜率和截距，以及相關系數。

slope, intercept, r, p, stderr = scipy.stats.linregress(x, y)

構建線性回歸公式。

line = f' y={intercept:.2f}+{slope:.2f}x, r={r:.2f}'
line
'y=-85.93+7.44x, r=0.76'

.plot() 繪圖

fig, ax = plt.subplots()
ax.plot(x, y, linewidth=0, marker='s', label='Data points')
ax.plot(x, intercept + slope * x, label=line)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(facecolor='white')
plt.show()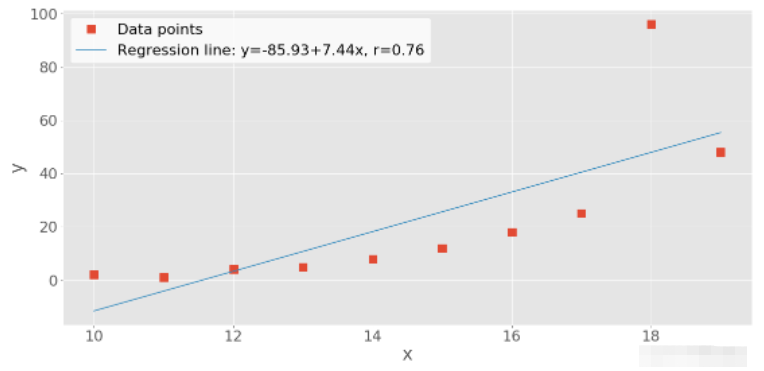

相關矩陣的熱圖 matplotlib

處理特征較多的相關矩陣用熱圖方式比較理想。

corr_matrix = np.corrcoef(xyz).round(decimals=2)
corr_matrix
array([[ 1.  ,  0.76, -0.97],
       [ 0.76,  1.  , -0.83],
       [-0.97, -0.83,  1.  ]])

其中為了表示方便將相關的數據四舍五入后用 .imshow() 繪制。

fig, ax = plt.subplots()
im = ax.imshow(corr_matrix)
im.set_clim(-1, 1)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1, 2), ticklabels=('x', 'y', 'z'))
ax.yaxis.set(ticks=(0, 1, 2), ticklabels=('x', 'y', 'z'))
ax.set_ylim(2.5, -0.5)
for i in range(3):
    for j in range(3):
        ax.text(j, i, corr_matrix[i, j], ha='center', va='center',
                color='r')
cbar = ax.figure.colorbar(im, ax=ax, format='% .2f')
plt.show()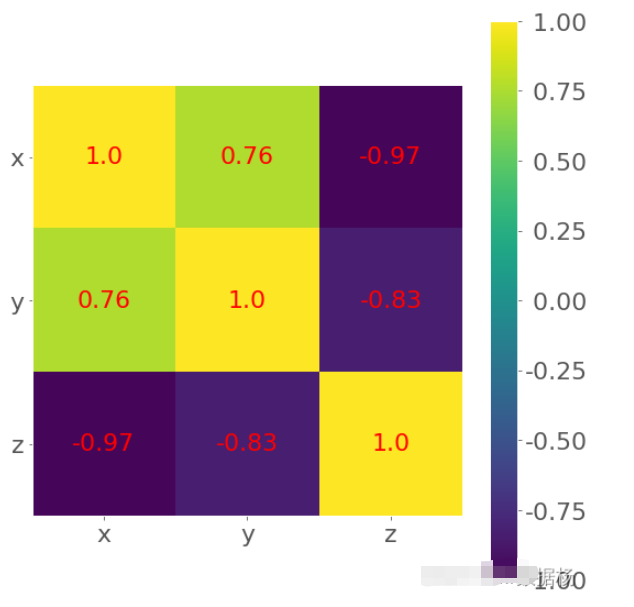

相關矩陣的熱圖 seaborn

import seaborn as sns

plt.figure(figsize=(11, 9),dpi=100)
sns.heatmap(data=corr_matrix,
            annot_kws={'size':8,'weight':'normal', 'color':'#253D24'},#數字屬性設置，例如字號、磅值、顏色        
           )

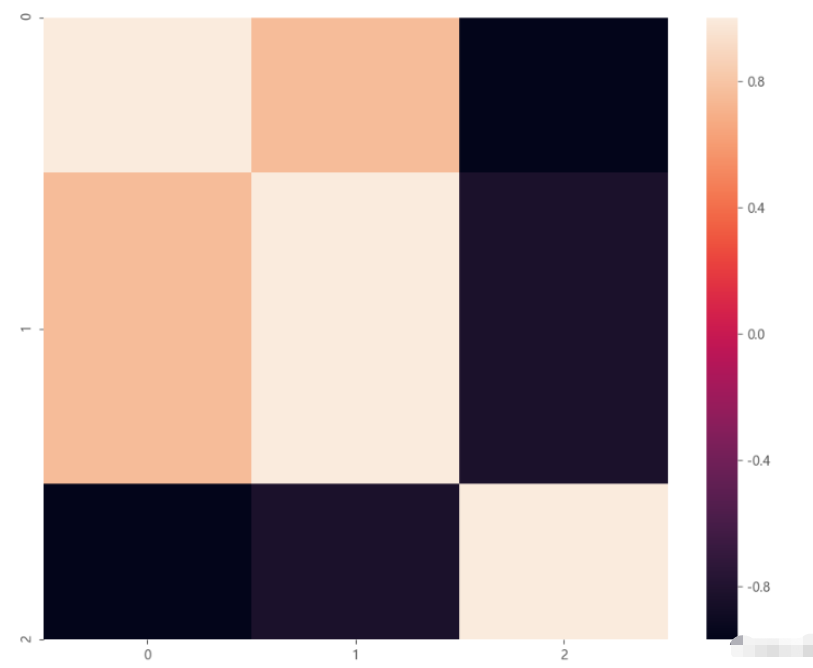
讀到這里，這篇“Python進行數據相關性分析的三種方式是什么”文章已經介紹完畢，想要掌握這篇文章的知識點還需要大家自己動手實踐使用過才能領會，如果想了解更多相關內容的文章，歡迎關注億速云行業資訊頻道。