如何用Python對數據進行相關性分析

這期內容當中小編將會給大家帶來有關如何用Python對數據進行相關性分析，文章內容豐富且以專業的角度為大家分析和敘述，閱讀完這篇文章希望大家可以有所收獲。

在進行數據分析時，我們所用到的數據往往都不是一維的，而這些數據在分析時難度就增加了不少，因為我們需要考慮維度之間的關系。而這些維度關系的分析就需要用一些方法來進行衡量，相關性分析就是其中一種。本文就用python來解釋一下數據的相關性分析。

在進行相關性分析之前需要介紹幾個概念，一是維度，二是協方差，三是相關系數。首先來看維度，以圖1為例，這是一個員工信息統計表，這里有n個員工，分別是員工1、員工2、......、員工n，每個員工有5個屬性，分別是身高、體重、年齡、工齡和學歷。每個員工的信息都是一個觀測，也叫一個樣品，本文就統稱觀測，每個員工的一個屬性叫一個指標，也叫變量、維度或者屬性，本文統稱維度。所以這個圖中就有n個觀測和5個維度。

圖1. 員工信息表

而協方差的定義就是E{ [ X - E(X) ] [ Y - E(Y) ] }，記作Cov(X, Y)，也就是兩個維度與各自期望之差的乘積的期望，期望在離散型數據中通常是均值，比如圖1中身高代表X，體重代表Y，E(X)就是身高的均值，E(Y)就是體重的均值，在利用二者分別和E(X)與E(Y)的差求協方差。而相關系數就是Cov(X, Y)/[σ(X)σ(Y)]，記作ρXY，其中σ(X)和σ(Y)分別表示X和Y的標準差，所以相關系數就是兩個變量的協方差除以其標準差之積。類似的，假如某個觀測有p個維度，計算每個維度同所有維度之間的協方差，則會形成一個pxp的矩陣，矩陣的每個數是其相應維度之間的協方差，這個矩陣就稱為協方差矩陣，協方差矩陣按照上面的方法再進一步計算就可得到相關關系矩陣。

下面就以python代碼來解釋一下相關性分析。

首先是數據集，本文用的數據來自繪圖庫seaborn自帶的數據，是非常著名的鳶尾花的數據，獲取方式非常簡單，執行下面代碼即可。這里有一個問題要提示一下，部分人在load_dataset時會出錯，無法讀取數據，是因為iris這個數據集不存在，這可能是因為seaborn版本的問題，如果遇到這種情況，可以去seaborn的GitHub數據網站自行下載數據，網址是https://github.com/mwaskom/seaborn-data，把下載的數據解壓到seaborn-data文件夾即可，這個文件夾一般在seaborn安裝目錄下或者是當前工作目錄下。

import seaborn as sns  data = sns.load_dataset('iris')  df = data.iloc[:, :4] #取前四列數據

這次用到的數據集共有150行、5列，我們只用到前4列數據。數據集樣例如圖2所示。

圖2. 數據集樣例

接下來我們來進行相關性分析。

首先來做一個比較簡單的分析，即分析這個數據集中第1列和第3列的相關性，也就是sepal_length和petal_length這兩列之間的關系。這里我們可以用numpy、scipy和pandas三種方法。首先是numpy。

import numpy as np  X = df['sepal_length']  Y = df['petal_length']  result1 = np.corrcoef(X, Y)

得到的result1結果就是一個二維矩陣，如圖3所示。

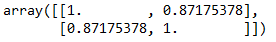
圖3. result1計算結果

其中矩陣主對角線上的數值都為1（主對角線就是從左上角到右下角的那條斜線），這是因為主對角線的數值都是每個觀測與自己的相關性，所以都是1，畢竟X=1X，Y=1Y，每個觀測都等于1乘以自身。而圖3中其他不為1的數字就是相關關系數值，一共有兩個，這兩個值相等，因為這兩個值分別表示ρXY和ρYX，其值相等。同理我們可以求df中4個維度的相關關系，代碼如下，這里rowvar代表以列為維度。

result2 = np.corrcoef(df, rowvar=False)

其結果如圖4所示。

圖4. result2計算結果

圖4是一個4x4的矩陣，共16個數據，代表每個維度同其他維度的相關關系（也包括每個維度與其自身），主對角線為1，其他數字關于主對角線對稱，是一個對稱矩陣。

接下來我們用scipy進行分析。代碼如下。

import scipy.stats as ss  result3 = ss.pearsonr(X, Y)

這個結果是(0.8717537758865831, 1.0386674194498099e-47)，其返回的是兩個數，第一個數是X和Y的相關關系數值，其值和前面numpy的計算結果相同，第二個是兩者不相關的概率，也就是我們統計學中常說的p值，但這個值是指不相關的概率，也就是值越小，代表越相關，我們這里的數值非常小，代表二者的線性相關程度比較大。當然如果相關關系數值為1，則p值為0。scipy中沒有計算相關矩陣的方法。

最后是pandas方法。

因為前面的df本身就是pandas的DataFrame格式，所以我們可以直接拿來用。代碼如下。

result4 = X.corr(Y)  result5 = df.corr()

result4結果是0.8717537758865833，result5結果如圖5所示。這兩個結果和前面所得的結果相同。

圖5. result5計算結果

接下來是作圖。對于分析相關關系，一般有兩種常見的圖形，一種是散點圖，一種是熱力圖。散點圖中可以清晰看到各個坐標點的分布及趨勢，對于數據分析者而言，其可以更直觀地了解各個維度數據之間的關系，但這種方法也有缺點，即不適合大數據量，因為數據量太大，生成圖片速度會很慢，同時圖片太多不利于觀察；而熱力圖則更多從數值或顏色方面，來準確描述各個維度的關系，其傳遞的信息較少，但比較適合大數據量。我們首先介紹一下散點圖。

生成散點圖可以用seaborn或者pandas。seaborn的代碼如下。

sns.pairplot(df)  sns.pairplot(df , hue ='sepal_width');

第一行代碼結果如圖6所示，是一張大圖，其中包含16個子圖，每個子圖都是每個維度和其他某個維度的相關關系圖，這其中主對角線上的圖，則是每個維度的數據分布直方圖。而第二行代碼是畫出同樣的圖形，但卻以sepal_width這個維度的數據為標準，來對各個數據點進行著色，其結果如圖7所示。從圖中可以看出，sepal_width這列數據共23個不同的數值，每個數值一種顏色，所以生成的圖是彩色的。

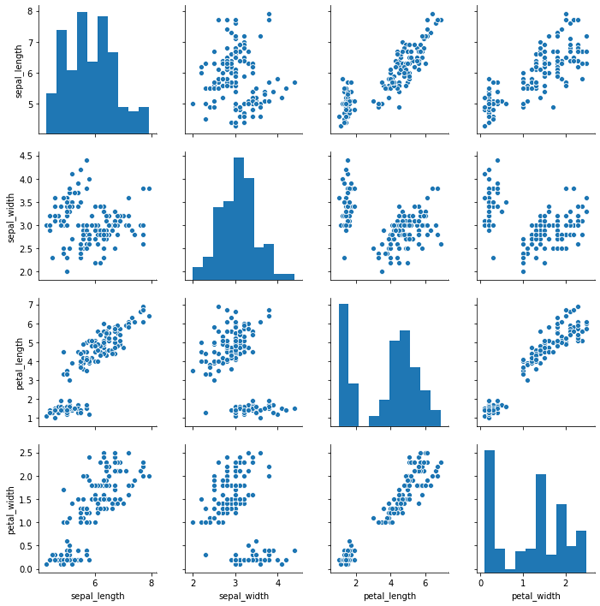
圖6. seaborn繪制的普通相關關系圖

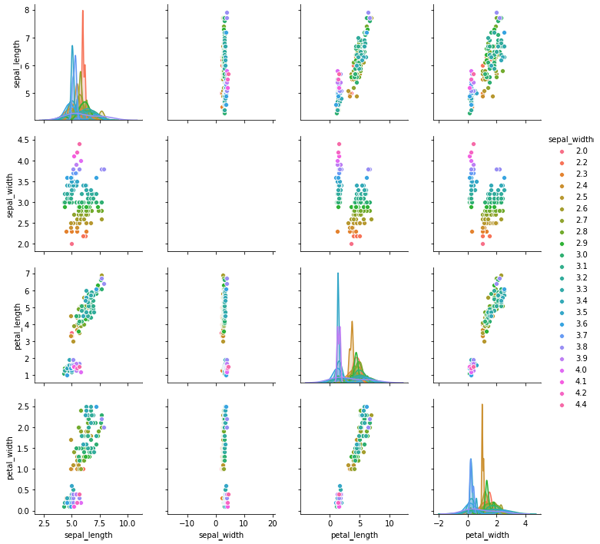
圖7. seaborn繪制的以某列數據為基準的相關關系圖

而另外一種繪圖方法是用pandas，其代碼如下。

import pandas as pd  pd.plotting.scatter_matrix(df, figsize=(12,12),range_padding=0.5);

結果如圖8所示，可以看到用pandas繪制的圖和seaborn的大體結果一樣，但圖片的可定制程度和精細度還是略差一些，所以一般情況下建議用seaborn。

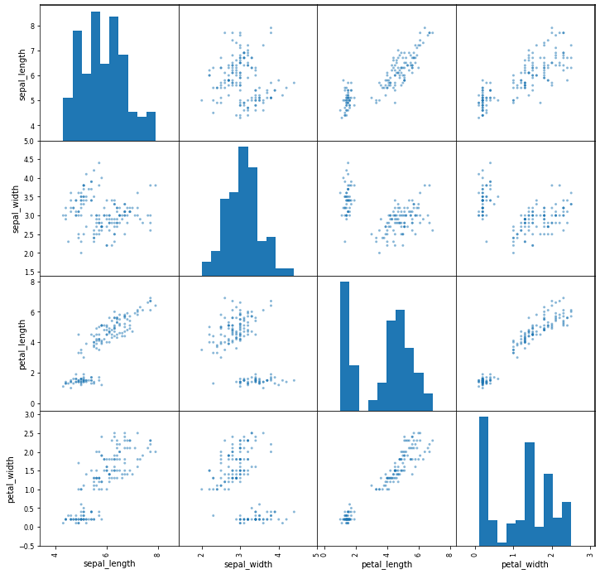
圖8. pandas生成的相關關系圖

最后就是熱力圖。其代碼如下。

import matplotlib.pyplot as plt  figure, ax = plt.subplots(figsize=(12, 12))  sns.heatmap(df.corr(), square=True, annot=True, axax=ax)

剛開始寫這段代碼時還出現了一個小問題，如圖9所示。圖9當中第一行和最后一行的子圖只顯示了一部分，而其他子圖都是完整顯示，這是matplotlib的一個bug，因為seaborn是基于matplotlib的庫，所以只要升級matplotlib就行了，剛開始筆者的matplotlib版本是3.1.1，現在已升級到3.2.2，這個bug已經被修復。正常圖如圖10所示。第二行代碼中square=True表示每個子圖是否以正方形顯示，這里設置為True，annot=True則表示是否在圖中顯示每個子圖的數值，這里同樣設置為True。

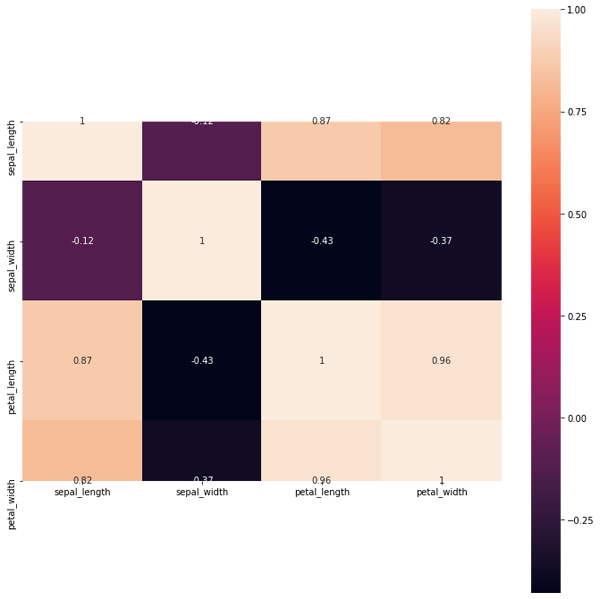
圖9. 老版本matplotlib生成的熱力圖

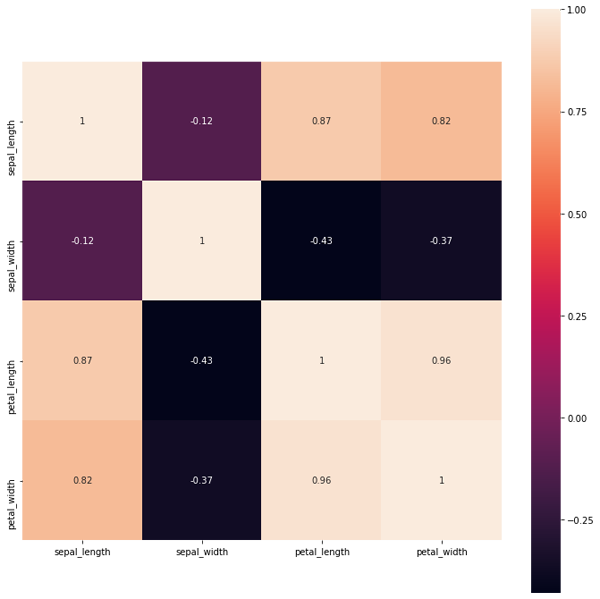
圖10. 新版本matplotlib生成的熱力圖

從數據計算到可視化，介紹了用python求多維數據間的相關關系的多種方法，我們可以根據自己的需求來選擇對應的方法。

上述就是小編為大家分享的如何用Python對數據進行相關性分析了，如果剛好有類似的疑惑，不妨參照上述分析進行理解。如果想知道更多相關知識，歡迎關注億速云行業資訊頻道。