您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關如何使用Python語言實現K-Means聚類算法的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
在一個典型的監督學習中,我們有一個有標簽的訓練集,我們的目標是找到能夠區分正
樣本和負樣本的決策邊界,在這里的監督學習中,我們有一系列標簽,我們需要據此擬合一
個假設函數。與此不同的是,在非監督學習中,我們的數據沒有附帶任何標簽,我們拿到的
數據就是這樣的:
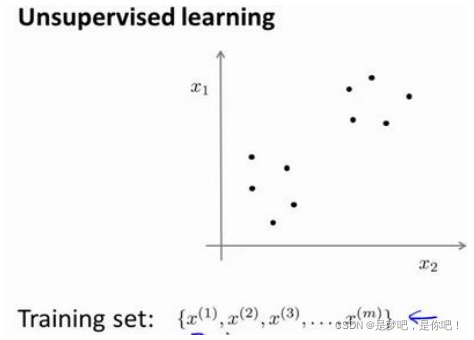
在這里我們有一系列點,卻沒有標簽。因此,我們的訓練集可以寫成只有:
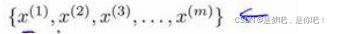
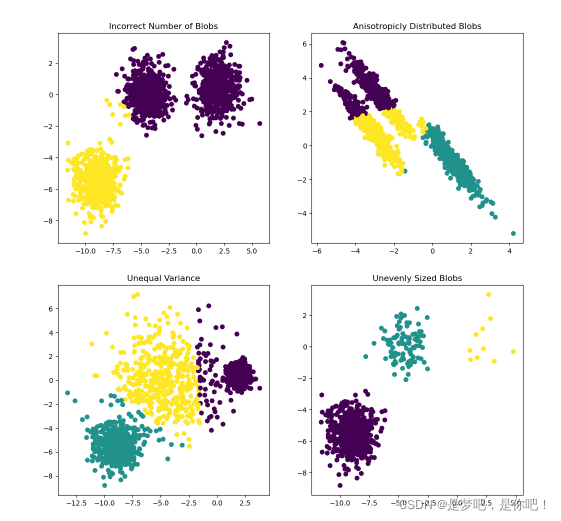
我們沒有任何標簽?。因此,圖上畫的這些點沒有標簽信息。也就是說,在非監 督學習中,我們需要將一系列無標簽的訓練數據,輸入到一個算法中,然后我們告訴這個算法,快去為我們找找這個數據的內在結構給定數據。我們可能需要某種算法幫助我們尋找一 種結構。圖上的數據看起來可以分成兩個分開的點集(稱為簇), 一個能夠找到我圈出的這 些點集的算法,就被稱為聚類算法 。
這將是我們介紹的第一個非監督學習算法。當然,此后我們還將提到其他類型的非監督
學習算法,它們可以為我們找到其他類型的結構或者其他的一些模式,而不只是簇。
我們將先介紹聚類算法。此后,我們將陸續介紹其他算法。那么聚類算法一般用來做什
么呢?

比如市場分割。也許你在數據庫中存儲了許多客戶的信息,而你希望將他們分成不同的客戶群,這樣你可以對不同類型的客戶分別銷售產品或者分別提供更適合的服務。社交網絡分析:事實上有許多研究人員正在研究這樣一些內容,他們關注一群人,關注社交網絡,例如 Facebook , Google+,或者是其他的一些信息,比如說:你經常跟哪些人聯系,而這些人又經常給哪些人發郵件,由此找到關系密切的人群。因此,這可能需要另一個聚類算法,你希望用它發現社交網絡中關系密切的朋友。 研究這個問題,希望使用聚類算法來更好的組織計算機集群,或者更好的管理數據中心。因為如果你知道數據中心中,那些計算機經常協作工作。那么,你可以重新分配資源,重新布局網絡。由此優化數據中心,優化數據通信。
最后,我實際上還在研究如何利用聚類算法了解星系的形成。然后用這個知識,了解一
些天文學上的細節問題。好的,這就是聚類算法。這將是我們介紹的第一個非監督學習算法,接下來,我們將開始介紹一個具體的聚類算法。
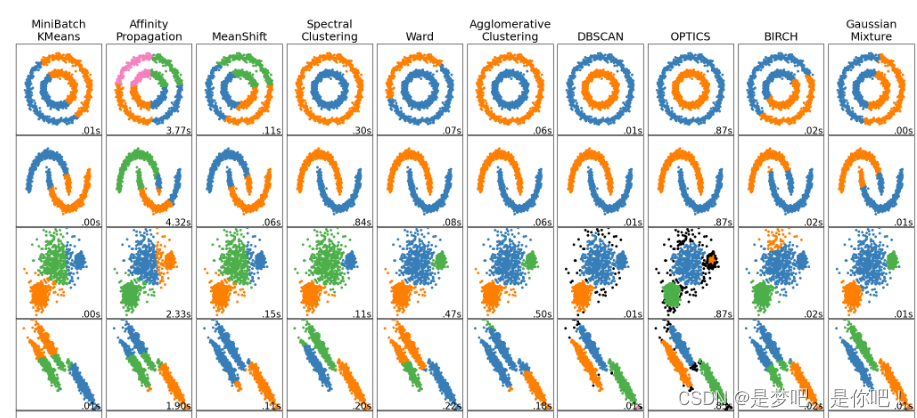

K- 均值 是最普及的聚類算法,算法接受一個未標記的數據集,然后將數據聚類成不同的
組
步驟:
設定 K 個類別的中心的初值;
計算每個樣本到 K個中心的距離,按最近距離進行分類;
以每個類別中樣本的均值,更新該類別的中心;
重復迭代以上步驟,直到達到終止條件(迭代次數、最小平方誤差、簇中心點變化率)。
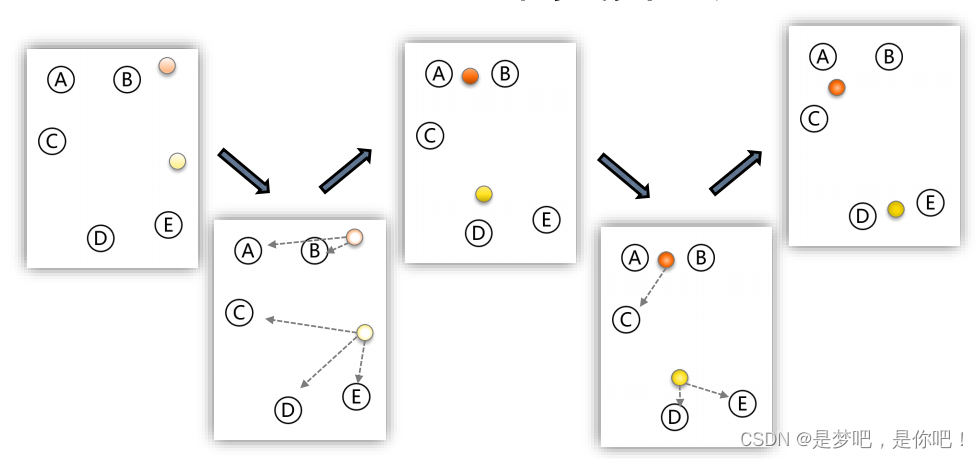
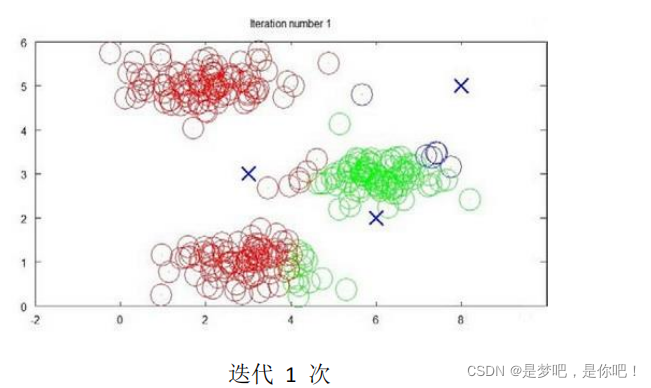
下面是一個聚類示例:
K-means聚類算法:
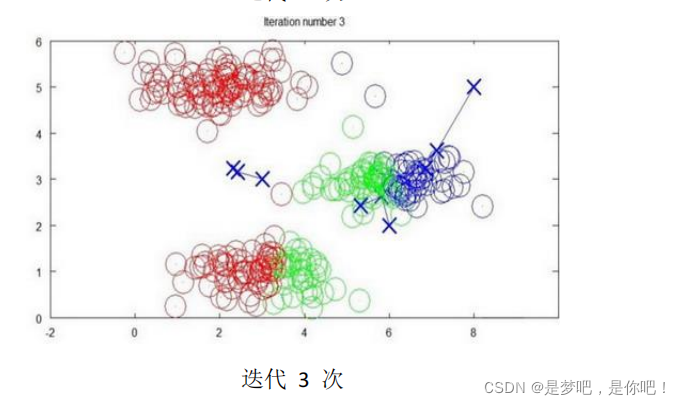

K-均值算法的偽代碼如下:
Repeat {
for i = 1 to m
c(i) := index (form 1 to K) of cluster centroid closest to x(i)
for k = 1 to K
μk := average (mean) of points assigned to cluster k
}算法分為兩個步驟,第一個 for 循環是賦值步驟,即:對于每一個樣例 i ,計算其應該屬
于的類。第二個 for 循環是聚類中心的移動,即:對于每一個類K ,重新計算該類的質心。
from sklearn.cluster import KMeans # 導入 sklearn.cluster.KMeans 類
import numpy as np
X = np.array([[1,2], [1,4], [1,0], [10,2], [10,4], [10,0]])
kmCluster = KMeans(n_clusters=2).fit(X) # 建立模型并進行聚類,設定 K=2
print("聚類中心坐標:",kmCluster.cluster_centers_) # 返回每個聚類中心的坐標
print("分類結果:",kmCluster.labels_) # 返回樣本集的分類結果
print("顯示預測判斷:",kmCluster.predict([[0, 0], [12, 3]])) # 根據模型聚類結果進行預測判斷聚類中心坐標: [[10. 2.] [ 1. 2.]] 分類結果: [1 1 1 0 0 0] 顯示預測判斷: [1 0] Process finished with exit code 0
對于樣本集巨大的問題,例如樣本量大于 10萬、特征變量大于100,K-Means算法耗費的速度和內存很大。SKlearn 提供了針對大樣本集的改進算法Mini Batch K-Means,并不使用全部樣本數據,而是每次抽樣選取小樣本集進行 K-Means聚類,進行循環迭代。Mini Batch K-Means 雖然性能略有降低,但極大的提高了運行速度和內存占用。
from sklearn.cluster import MiniBatchKMeans # 導入 .MiniBatchKMeans 類
import numpy as np
X = np.array([[1,2], [1,4], [1,0], [4,2], [4,0], [4,4],
[4,5], [0,1], [2,2],[3,2], [5,5], [1,-1]])
# fit on the whole data
mbkmCluster = MiniBatchKMeans(n_clusters=3,batch_size=6,max_iter=10).fit(X)
print("聚類中心的坐標:",mbkmCluster.cluster_centers_) # 返回每個聚類中心的坐標
print("樣本集的分類結果:",mbkmCluster.labels_) # 返回樣本集的分類結果
print("顯示判斷結果:樣本屬于哪個類別:",mbkmCluster.predict([[0,0], [4,5]])) # 根據模型聚類結果進行預測判斷聚類中心的坐標: [[ 2.55932203 1.76271186] [ 0.75862069 -0.20689655] [ 4.20588235 4.5 ]] 樣本集的分類結果: [0 0 1 0 0 2 2 1 0 0 2 1] 顯示判斷結果:樣本屬于哪個類別: [1 2] Process finished with exit code 0
from sklearn.cluster import kmeans_plusplus
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# Generate sample data
n_samples = 4000
n_components = 4
X, y_true = make_blobs(
n_samples=n_samples, centers=n_components, cluster_std=0.60, random_state=0
)
X = X[:, ::-1]
# Calculate seeds from kmeans++
centers_init, indices = kmeans_plusplus(X, n_clusters=4, random_state=0)
# Plot init seeds along side sample data
plt.figure(1)
colors = ["#4EACC5", "#FF9C34", "#4E9A06", "m"]
for k, col in enumerate(colors):
cluster_data = y_true == k
plt.scatter(X[cluster_data, 0], X[cluster_data, 1], c=col, marker=".", s=10)
plt.scatter(centers_init[:, 0], centers_init[:, 1], c="b", s=50)
plt.title("K-Means++ Initialization")
plt.xticks([])
plt.yticks([])
plt.show()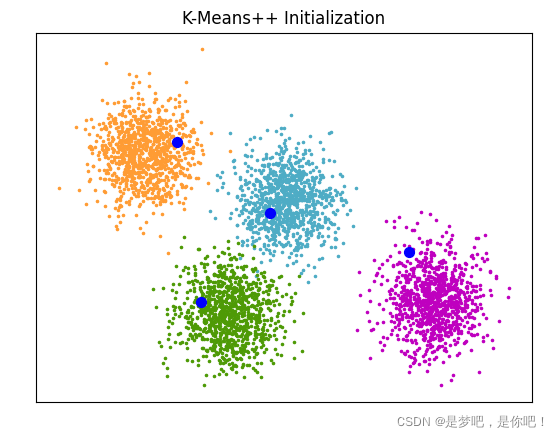
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
from sklearn.cluster import KMeans, MiniBatchKMeans
def main():
# 讀取數據文件
file = pd.read_excel('K-Means.xlsx', header=0) # 首行為標題行
file = file.dropna() # 刪除含有缺失值的數據
# print(file.dtypes) # 查看 df 各列的數據類型
# print(file.shape) # 查看 df 的行數和列數
print(file.head())
# 數據準備
z_scaler = lambda x:(x-np.mean(x))/np.std(x) # 定義數據標準化函數
dfScaler = file[['D1','D2','D3','D4','D5','D6','D7','D8','D9','D10']].apply(z_scaler) # 數據歸一化
dfData = pd.concat([file[['地區']], dfScaler], axis=1) # 列級別合并
df = dfData.loc[:,['D1','D2','D3','D4','D5','D6','D7','D8','D9','D10']] # 基于全部 10個特征聚類分析
# df = dfData.loc[:,['D1','D2','D7','D8','D9','D10']] # 降維后選取 6個特征聚類分析
X = np.array(df) # 準備 sklearn.cluster.KMeans 模型數據
print("Shape of cluster data:", X.shape)
# KMeans 聚類分析(sklearn.cluster.KMeans)
nCluster = 4
kmCluster = KMeans(n_clusters=nCluster).fit(X) # 建立模型并進行聚類,設定 K=4
print("Cluster centers:\n", kmCluster.cluster_centers_) # 返回每個聚類中心的坐標
print("Cluster results:\n", kmCluster.labels_) # 返回樣本集的分類結果
# 整理聚類結果(太棒啦!)
listName = dfData['地區'].tolist() # 將 dfData 的首列 '地區' 轉換為 list
dictCluster = dict(zip(listName,kmCluster.labels_)) # 將 listName 與聚類結果關聯,組成字典
listCluster = [[] for k in range(nCluster)]
for v in range(0, len(dictCluster)):
k = list(dictCluster.values())[v] # 第v個城市的分類是 k
listCluster[k].append(list(dictCluster.keys())[v]) # 將第v個城市添加到 第k類
print("\n聚類分析結果(分為{}類):".format(nCluster)) # 返回樣本集的分類結果
for k in range(nCluster):
print("第 {} 類:{}".format(k, listCluster[k])) # 顯示第 k 類的結果
return
if __name__ == '__main__':
main()地區 D1 D2 D3 D4 D5 D6 D7 D8 D9 D10
0 北京 5.96 310 461 1557 931 319 44.36 2615 2.20 13631
1 上海 3.39 234 308 1035 498 161 35.02 3052 0.90 12665
2 天津 2.35 157 229 713 295 109 38.40 3031 0.86 9385
3 陜西 1.35 81 111 364 150 58 30.45 2699 1.22 7881
4 遼寧 1.50 88 128 421 144 58 34.30 2808 0.54 7733
Shape of cluster data: (30, 10)
Cluster centers:
[[-3.04626787e-01 -2.89307971e-01 -2.90845727e-01 -2.88480032e-01
-2.85445404e-01 -2.85283077e-01 -6.22770669e-02 1.12938023e-03
-2.71308432e-01 -3.03408599e-01]
[ 4.44318512e+00 3.97251590e+00 4.16079449e+00 4.20994153e+00
4.61768098e+00 4.65296699e+00 2.45321197e+00 4.02147595e-01
4.22779099e+00 2.44672575e+00]
[ 1.52987871e+00 2.10479182e+00 1.97836141e+00 1.92037518e+00
1.54974999e+00 1.50344182e+00 1.13526879e+00 1.13595799e+00
8.39397483e-01 1.38149832e+00]
[ 4.17353928e-01 -6.60092295e-01 -5.55528420e-01 -5.50211065e-01
-2.95600461e-01 -2.42490616e-01 -3.10454580e+00 -2.70342746e+00
1.14743326e+00 2.67890118e+00]]
Cluster results:
[1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0]
聚類分析結果(分為4類):
第 0 類:['陜西', '遼寧', '吉林', '黑龍江', '湖北', '江蘇', '廣東', '四川', '山東', '甘肅', '湖南', '浙江', '新疆', '福建', '山西', '河北', '安徽', '云南', '江西', '海南', '內蒙古', '河南', '廣西', '寧夏', '貴州', '青海']
第 1 類:['北京']
第 2 類:['上海', '天津']
第 3 類:['西藏']
Process finished with exit code 0
(1)數據介紹:
現有1999年全國31個省份城鎮居民家庭平均每人全年消費性支出的八個主要變量數據,這八個變量分別是:食品、衣著、家庭設備用品及服務、醫療保健、交通和通訊、娛樂教育文化服務、居住以及雜項商品和服務。利用已有數據,對31個省份進行聚類。
(2)實驗目的:
通過聚類,了解 1999 年各個省份的消費水平在國內的情況
1999年全國31個省份城鎮居民家庭平均每人全年消費性支出數據:

#*========================1. 建立工程,導入sklearn相關包======================================**
import numpy as np
from sklearn.cluster import KMeans
#*======================2. 加載數據,創建K-means算法實例,并進行訓練,獲得標簽====================**
def loadData(filePath):
fr = open(filePath, 'r+') #r+:讀寫打開一個文本文件
lines = fr.readlines() #.readlines() 一次讀取整個文件(類似于 .read() ) .readline() 每次只讀.readlines() 慢得多。
retData = [] #retData:用來存儲城市的各項消費信息
retCityName = [] #retCityName:用來存儲城市名稱
for line in lines:
items = line.strip().split(",")
retCityName.append(items[0])
retData.append([float(items[i]) for i in range(1, len(items))])
return retData, retCityName #返回值:返回城市名稱,以及該城市的各項消費信息
def main():
data, cityName = loadData('city.txt') #1.利用loadData方法讀取數據
km = KMeans(n_clusters=4) #2.創建實例
label = km.fit_predict(data) #3.調用Kmeans()fit_predict()方法進行計算
expenses = np.sum(km.cluster_centers_, axis=1)
# print(expenses)
CityCluster = [[], [], [], []] #將城市按label分成設定的簇
for i in range(len(cityName)):
CityCluster[label[i]].append(cityName[i]) #將每個簇的城市輸出
for i in range(len(CityCluster)): #將每個簇的平均花費輸出
print("Expenses:%.2f" % expenses[i])
print(CityCluster[i])
if __name__ == '__main__':
main()
#*=============3. 輸出標簽,查看結果========================================**
#將城市按照消費水平n_clusters類,消費水平相近的城市聚集在一類中
#expense:聚類中心點的數值加和,也就是平均消費水平
(1)聚成2類:km = KMeans(n_clusters=2)

(2)聚成3類:km = KMeans(n_clusters=3)

(3)聚成4類:km = KMeans(n_clusters=4)

從結果可以看出消費水平相近的省市聚集在了一類,例如消費最高的“北京”“上海”“廣東”
聚集在了消費最高的類別。聚4類時,結果可以比較明顯的看出消費層級。
計算兩條數據相似性時,Sklearn 的K-Means默認用的是歐式距離。雖然還有余弦相似度,馬氏距離等多種方法,但沒有設定計算距離方法的參數。
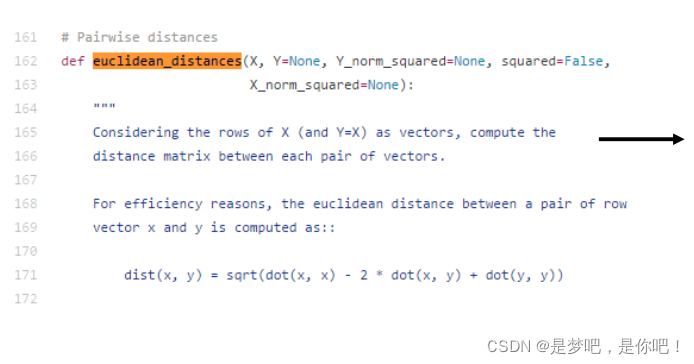
(1)如果想要自定義計算距離的方式時,可以更改此處源碼。
(2)建議使用 scipy.spatial.distance.cdist 方法。
使用形式:scipy.spatial.distance.cdist(A, B, metric=‘cosine’):

重要參數:
A:A向量
B:B向量
metric: 計算A和B距離的方法,更改此參數可以更改調用的計算距離的方法
感謝各位的閱讀!關于“如何使用Python語言實現K-Means聚類算法”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。