Python機器學習之邏輯回歸的示例分析

這篇文章主要介紹了Python機器學習之邏輯回歸的示例分析，具有一定借鑒價值，感興趣的朋友可以參考下，希望大家閱讀完這篇文章之后大有收獲，下面讓小編帶著大家一起了解一下。

Python主要用來做什么

Python主要應用于：1、Web開發；2、數據科學研究；3、網絡爬蟲；4、嵌入式應用開發；5、游戲開發；6、桌面應用開發。

一、題目

1.主題：邏輯回歸

2.描述：假設你是某大學招生主管，你想根據兩次考試的結果決定每個申請者的錄取
機會。現有以往申請者的歷史數據，可以此作為訓練集建立邏輯回歸模型，并用
其預測某學生能否被大學錄取。

3.數據集：文件 ex2data1.txt ，第一列、第二列分別表示申請者兩次
考試的成績，第三列表示錄取結果（1 表示錄取，0 表示不錄取）。

二、目的

1.理解邏輯回歸模型

2.掌握邏輯回歸模型的參數估計算法

三、平臺

1.硬件：計算機

2.操作系統：WINDOWS

3.編程軟件：Pycharm

4.開發語言：python

四、基本原理

注：基本原理是我們在學習邏輯回歸過程中的一些總結，包括為什么要選擇對數損失函數等。

4.1 邏輯回歸

邏輯回歸就是將樣本的特征可樣本發生的概率聯合起來，概率就是一個數，所以就是解決分類問題，一般解決二分類問題。
對于線性回歸中，f ( x ) = w T x + b ，這里 f ( x ) 的范圍為[ ? ∞ , + ∞ ]，說明通過線性回歸中我們可以求得任意的一個值。對于邏輯回歸來說就是概率，這個概率取值需要在區間[0,1]內，通常我們使用Sigmoid函數表示。

Sigmoid函數其表達式為（2）

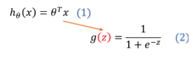
最終我們可以通過Sigmoid函數求出對于每組自變量使得因變量預測為1的概率P；

即：

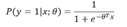
（當P>0.5時預測為1，小于0.5為0）
在分類情況下，經過學習后的LR分類器其實就是一組權值θ ，當有測試樣本輸入時，這組權值與測試數據按照加權得到

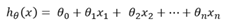
之后按照Sigmoid函數的形式求出

從而去判斷每個測試樣本所屬的類別。

4.2 損失函數

實驗一我們做線性回歸模型時，給出了線性回歸的代價函數的形式（誤差平方和函數），具體形式如：

但是并不能應用到邏輯回歸中，這是因為LR的假設函數的外層函數是Sigmoid函數，Sigmoid函數是一個復雜的非線性函數，這就使得我們將邏輯回歸的假設函數

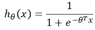
帶入上式時，我們得到的 是一個非凸函數，如下圖：

因此，此處我們需要重新考慮損失函數；
在邏輯回歸中，我們最常用的損失函數為對數損失函數，對數損失函數可以為LR提供一個凸的代價函數，有利于使用梯度下降對參數求解。對數函數圖像如圖：

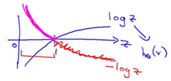
藍色的曲線表示的是對數函數的圖像，紅色的曲線表示的是負對數 的圖像，該圖像在0-1區間上有一個很好的性質，如圖粉紅色曲線部分。在0-1區間上當z=1時，函數值為0，而z=0時，函數值為無窮大。這就可以和代價函數聯系起來，在預測分類中當算法預測正確其代價函數應該為0；當預測錯誤，我們就應該用一個很大代價（無窮大）來懲罰我們的學習算法，使其不要輕易預測錯誤。
因此，我們重新定義邏輯回歸的代價函數為：

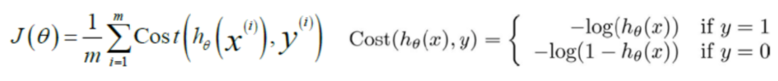
損失函數的求解為：

五、實驗步驟

1.數據可視化

在python中通過文件導入數據，并使用matlibplot工具建立對應散點圖：

需要注意的是，我們的theta是三元組，θ0對應的X特征值固定為1，因此讀取數據時，如上圖最左側加入一個1；

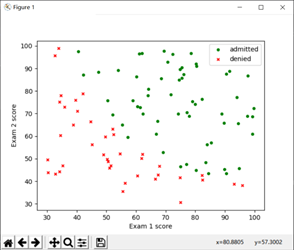
可以看到，被錄取與不被錄取的數據有較為清晰的一個界限，接下來我們要求解的就是這條界線；

2. 將線性回歸參數初始化為0，計算代價函數(cost function)的初始值

根據基本原理中的代價計算公式，這里將sigmoid、損失公式代碼化：

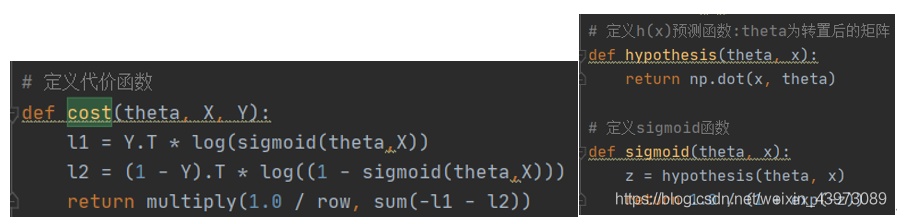
將theta初始化為（0，0，0）后，直接調用cost函數求值：

得到代價函數初始值：

3. 選擇一種優化方法求解邏輯回歸參數

梯度下降法

我們選擇先用梯度下降法來觀察theta參數結果；
梯度下降算法代碼實現如圖：

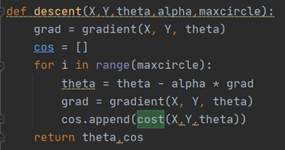
X：對于線性回歸中的常量b，我們可以將它的系數視為1，然后和變量x組成一個m行3列的矩陣，其中m是數據規模，這個矩陣就是X。
Y：一個m行1列的矩陣，對應是否錄取。
alpha：學習率
第一步，將我們的Θ初始化為[[0][0][0]]。
第二步，對于給定的步長alpha和此時的梯度gradient，更新我們的theta。然后計算此時thrta對應的梯度更新gradient。
第三步，重復第二步30萬次
第四步，返回theta，即為我們線性回歸的參數。

但是，對于邏輯回歸來說，這里遇到了一個問題，那就是alpha和迭代次數的取值，如果alpha過小，損失函數將收斂的非常慢，迭代次數達到40萬時才勉強收斂，但如果alpha過大，又會導致過大的步長使得準確率下降；
alpha = 0.001時的收斂函數，在50萬次時收斂： 0.005時在25萬次時收斂；

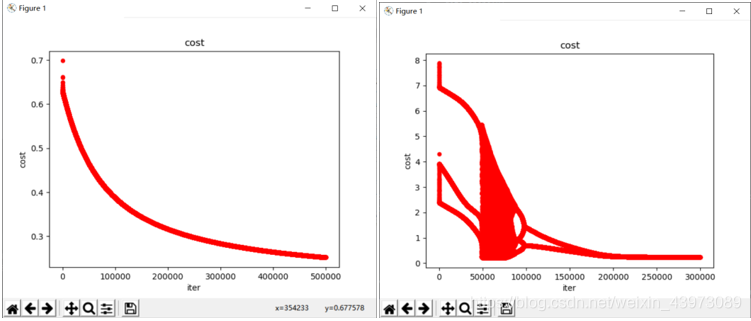
而如果alpha繼續增大（如0.01），將導致不夠準確，其界限與收斂圖形如下：

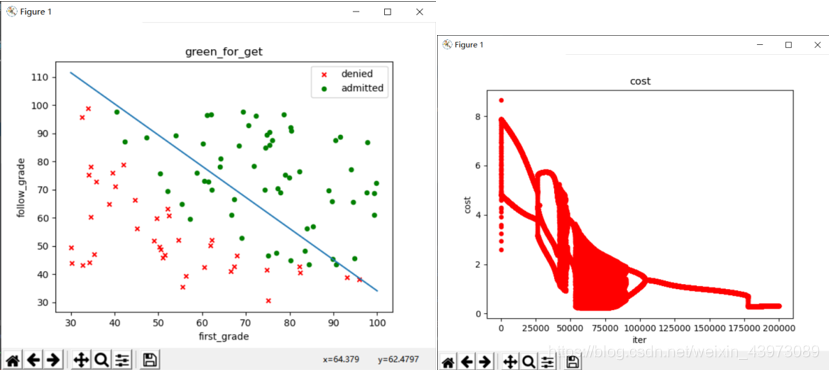
（界限太差，僅80%準確率，且需要20萬次迭代）
因此，我們在運行該數據時需要運行稍長的時間；alpha=0.005，迭代次數為30萬時可以得到一組回歸參數：

它的劃分邊界如圖所示，其準確率為92%：該參數的劃分準確率計算方法如下：

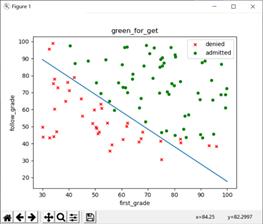
測試準確率：

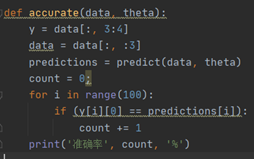
比較簡單，預測正確則加一，最后除以全部樣本數。

牛頓迭代法

因為上述的迭代下降法所需迭代次數過多，因此這里使用一種優化方法來求解參數；

方法介紹

牛頓迭代法的原理較為復雜，因此不在這里寫出來。
對比這牛頓迭代法方法與梯度下降法的參數更新公式可以發現，兩種方法不同在于牛頓法中多了一項二階導數，這項二階導數對參數更新的影響主要體現在 改變參數更新方向上。

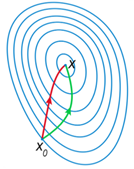
如圖所示，紅色是牛頓法參數更新的方向，綠色為梯度下降法參數更新方向，因為牛頓法考慮了二階導數，因而可以找到更優的參數更新方向，在每次更新的步幅相同的情況下，可以比梯度下降法節省很多的迭代次數。
迭代過程：

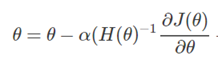
代碼實現

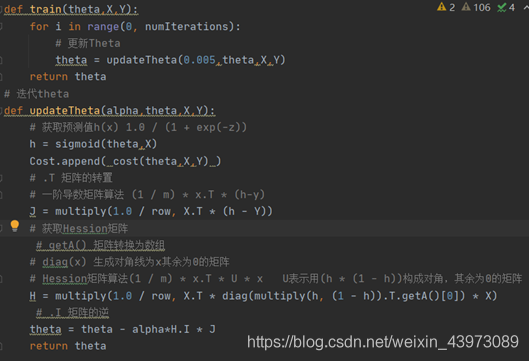
h值為sigmoid函數求得的概率；
J為一階偏導數
H為Hession矩陣（海森矩陣），二階偏導數

牛頓迭代法得到的theta：

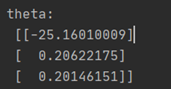
優點

對于同樣的學習率alpha = 0.005，cost僅需要1000次迭代就差不多收斂了；
而如果放大alpha，如alpha = 0.5，那么它只需要迭代10次即可收斂。

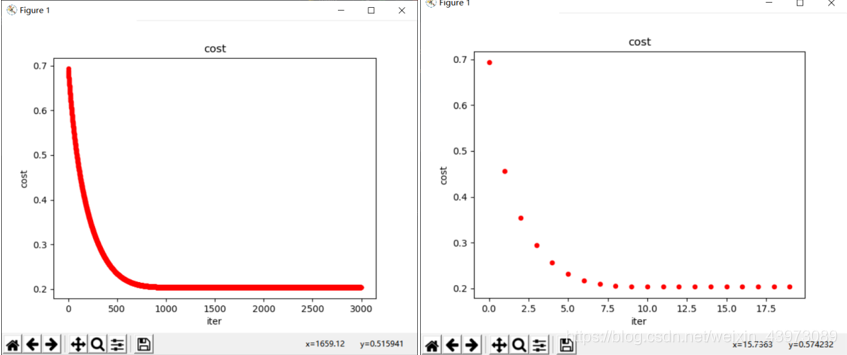
并且準確率保持在89%（數據較小）；

4. 某學生兩次考試成績分別為 42、85，預測其被錄取的概率

這里直接使用sigmoid函數以及牛頓迭代法求得的theta來進行其概率的計算：

得到結果：

即，y=1的概率為0.65145509，也就是被錄取的概率

5. 畫出分類邊界

在上面已經畫出了梯度下降法的分類邊界，這里給出牛頓迭代法的邊界

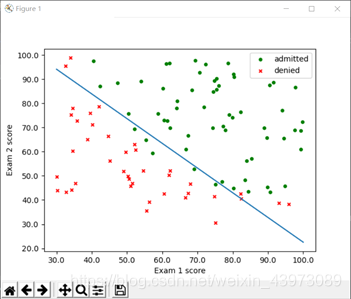
感謝你能夠認真閱讀完這篇文章，希望小編分享的“Python機器學習之邏輯回歸的示例分析”這篇文章對大家有幫助，同時也希望大家多多支持億速云，關注億速云行業資訊頻道，更多相關知識等著你來學習!