您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關python中邏輯回歸與非監督學習的示例分析,小編覺得挺實用的,因此分享給大家做個參考,希望大家閱讀完這篇文章后可以有所收獲。
模型訓練好之后,可以直接保存,需要用到joblib庫。保存的時候是pkl格式,二進制,通過dump方法保存。加載的時候通過load方法即可。
安裝joblib:conda install joblib
保存:joblib.dump(rf, 'test.pkl')
加載:estimator = joblib.load('模型路徑')
加載后直接將測試集代入即可進行預測。
邏輯回歸是一種分類算法,但該分類的標準,是通過h(x)輸入后,使用sigmoid函數進行轉換,同時根據閾值,就能夠針對不同的h(x)值,輸出0-1之間的數。我們將這個0-1之間的輸出,認為是概率。假設閾值是0.5,那么,大于0.5的我們認為是1,否則認為是0。邏輯回歸適用于二分類問題。
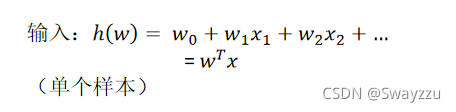
可以看出,輸入還是線性回歸的模型,里面還是有權重w,以及特征值x,我們的目標依舊是找出最合適的w。
該函數圖像如下:
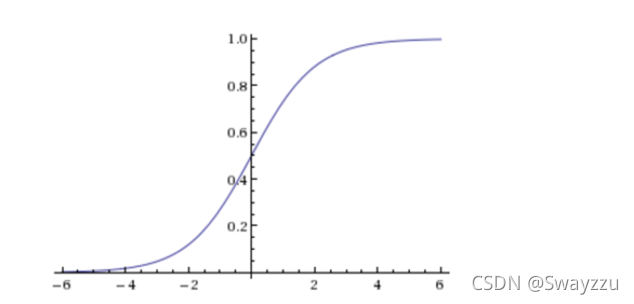
該函數公式如下:

z就是回歸的結果h(x),通過sigmoid函數的轉化,無論z是什么值,輸出都是在0-1之間。那么我們需要選擇最合適的權重w,使得輸出的概率及所得結果,能夠盡可能地貼近訓練集的目標值。因此,邏輯回歸也有一個損失函數,稱為對數似然損失函數。將其最小化,便可求得目標w。

損失函數在y=1和0的時候的函數圖像如下:
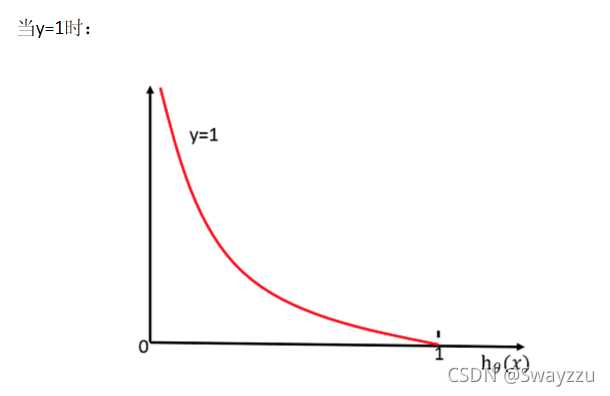
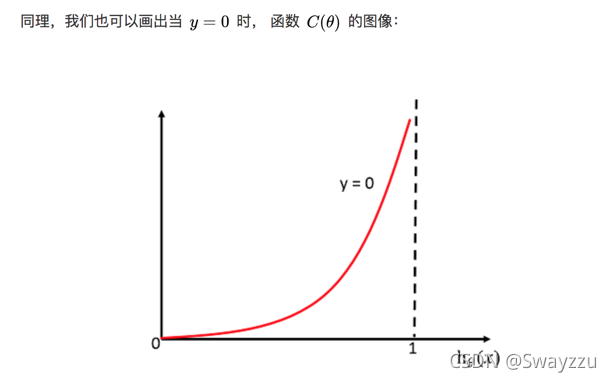
由上圖可看出,若真實值類別是1,則h(x)給出的輸出,越接近于1,損失函數越小,反之越大。當y=0時同理。所以可據此,當損失函數最小的時候,我們的目標就找到了。
邏輯回歸也是通過梯度下降進行的求解。對于均方誤差來說,只有一個最小值,不存在局部最低點;但對于對數似然損失,可能會出現多個局部最小值,目前沒有一個能完全解決局部最小值問題的方法。因此,我們只能通過多次隨機初始化,以及調整學習率的方法來盡量避免。不過,即使最后的結果是局部最優解,依舊是一個不錯的模型。
sklearn.linear_model.LogisticRegression

其中penalty是正則化方式,C是懲罰力度。
給定的數據中,是通過多個特征,綜合判斷腫瘤是否為惡性。
由于算法的流程基本一致,重點都在于數據和特征的處理,因此本文中不再詳細闡述,代碼如下:
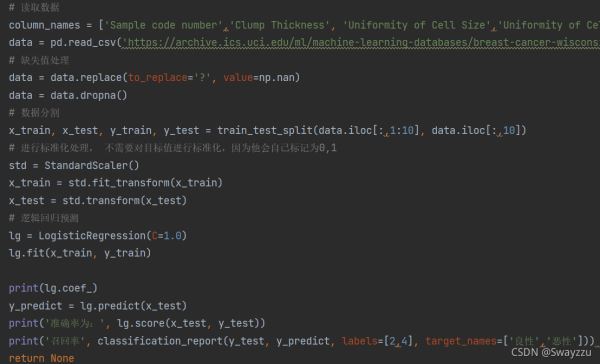
注意:
邏輯回歸的目標值不是0和1,而是2和4,但不需要進行處理,算法中會自動標記為0和1
算法預測完畢后,如果想看召回率,需要注意對所分的類別給出名字,但給名字之前需要先貼標簽。見上圖。否則方法不知道哪個是良性,哪個是惡性。貼標簽的時候順序需對應好。
一般情況下,哪個類別的樣本少,就按照哪個來去判定。比如惡性的少,就以“判斷屬于惡性的概率是多少”來去判斷
應用:廣告點擊率預測、是否患病等二分類問題
優點:適合需要得到一個分類概率的場景
缺點:當特征空間很大時,邏輯回歸的性能不是很好 (看硬件能力)
非監督學習就是,不給出正確答案。也就是說數據中沒有目標值,只有特征值。
假設聚類的類別為3類,流程如下:
①隨機在數據中抽取三個樣本,作為類別的三個中心點
②計算剩余的點分別道三個中心點的距離,從中選出距離最近的點作為自己的標記。形成三個族群
③分別計算這三個族群的平均值,把三個平均值與之前的三個中心點進行比較。如果相同,結束聚類,如果不同,把三個平均值作為新的聚類中心,重復第二步。
sklearn.cluster.KMeans

通常情況下,聚類是做在分類之前。先把樣本進行聚類,對其進行標記,接下來有新的樣本的時候,就可以按照聚類所給的標準進行分類。
簡單來說,就是類中的每一個點,與“類內的點”的距離,以及“類外的點”的距離。距離類內的點,越近越好。而距離類外的點,越遠越好。

如果sc_i 小于0,說明a_i 的平均距離大于最近的其他簇。 聚類效果不好
如果sc_i 越大,說明a_i 的平均距離小于最近的其他簇。 聚類效果好
輪廓系數的值是介于 [-1,1] ,越趨近于1代表內聚度和分離度都相對較優
sklearn.metrics.silhouette_score

聚類算法容易收斂到局部最優,可通過多次聚類解決。
關于“python中邏輯回歸與非監督學習的示例分析”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,使各位可以學到更多知識,如果覺得文章不錯,請把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。