您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
因為TreeMap的存儲結構是紅黑樹,我們回顧一下紅黑樹的特點以及基本操作。下圖為典型的紅黑樹: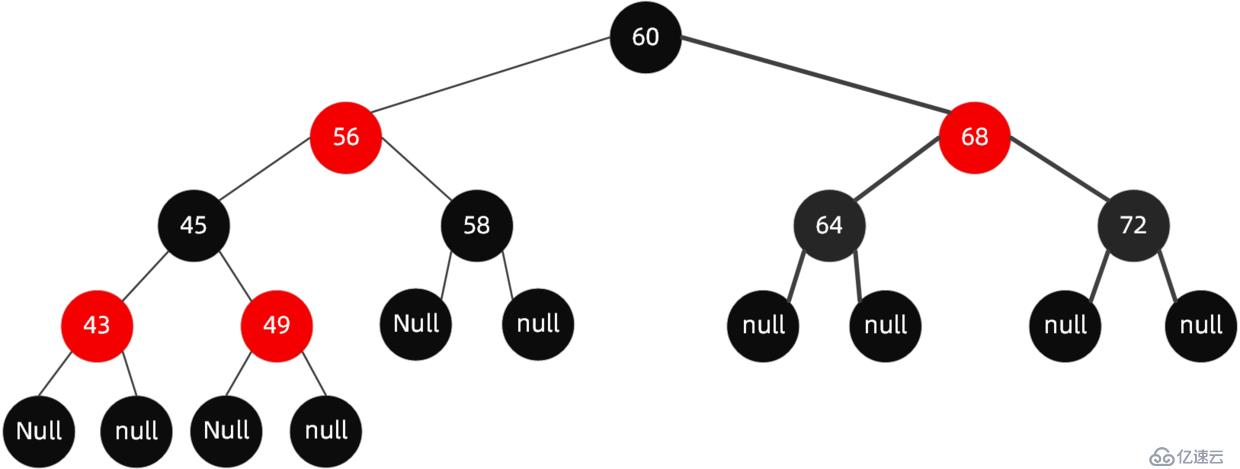
紅黑樹規則特點:
紅黑樹自平衡基本操作:
我們先看一下TreeMap中主要的成員變量
/**
* 我們前面提到TreeMap是可以自動排序的,默認情況下comparator為null,這個時候按照key的自然順序進行排
* 序,然而并不是所有情況下都可以直接使用key的自然順序,有時候我們想讓Map的自動排序按照我們自己的規則,
* 這個時候你就需要傳遞Comparator的實現類
*/
private final Comparator<? super K> comparator;
/**
* TreeMap的存儲結構既然是紅黑樹,那么必然會有唯一的根節點。
*/
private transient Entry<K,V> root;
/**
* Map中key-val對的數量,也即是紅黑樹中節點Entry的數量
*/
private transient int size = 0;
/**
* 紅黑樹結構的調整次數
*/
private transient int modCount = 0;上面的主要成員變量根節點root是Entry類的實體,我們來看一下Entry類的源碼
static final class Entry<K,V> implements Map.Entry<K,V> {
//key,val是存儲的原始數據
K key;
V value;
//定義了節點的左孩子
Entry<K,V> left;
//定義了節點的右孩子
Entry<K,V> right;
//通過該節點可以反過來往上找到自己的父親
Entry<K,V> parent;
//默認情況下為黑色節點,可調整
boolean color = BLACK;
/**
* 構造器
*/
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* 獲取節點的key值
*/
public K getKey() {return key;}
/**
* 獲取節點的value值
*/
public V getValue() {return value;}
/**
* 用新值替換當前值,并返回當前值
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}Entry靜態內部類實現了Map的內部接口Entry,提供了紅黑樹存儲結構的java實現,通過left屬性可以建立左子樹,通過right屬性可以建立右子樹,通過parent可以往上找到父節點。
大體的實現結構圖如下:
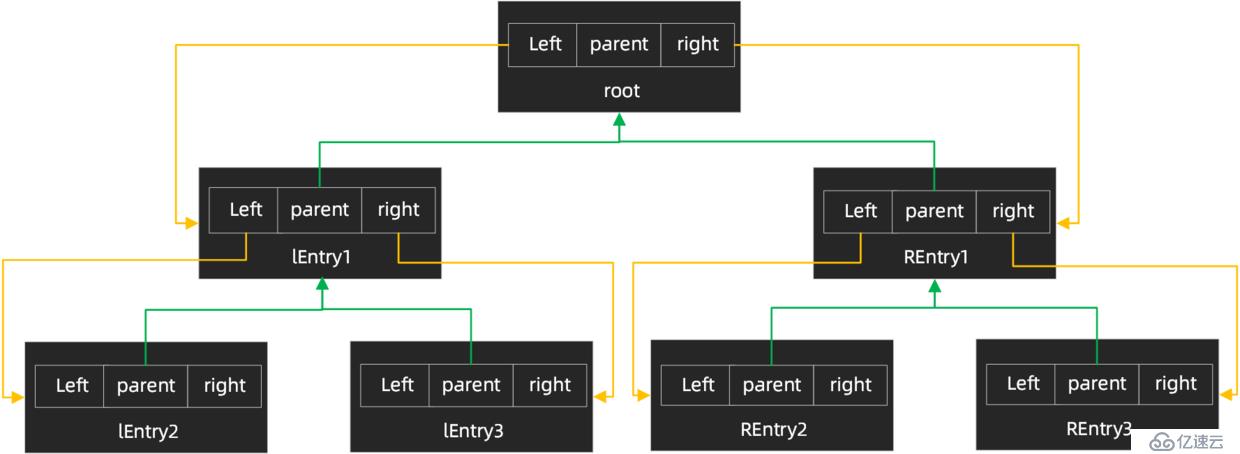
TreeMap構造函數:
//默認構造函數,按照key的自然順序排列
public TreeMap() {comparator = null;}
//傳遞Comparator具體實現,按照該實現規則進行排序
public TreeMap(Comparator<? super K> comparator) {this.comparator = comparator;}
//傳遞一個map實體構建TreeMap,按照默認規則排序
public TreeMap(Map<? extends K, ? extends V> m) {
comparator = null;
putAll(m);
}
//傳遞一個map實體構建TreeMap,按照傳遞的map的排序規則進行排序
public TreeMap(SortedMap<K, ? extends V> m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}put方法為Map的核心方法,TreeMap的put方法大概流程如下:
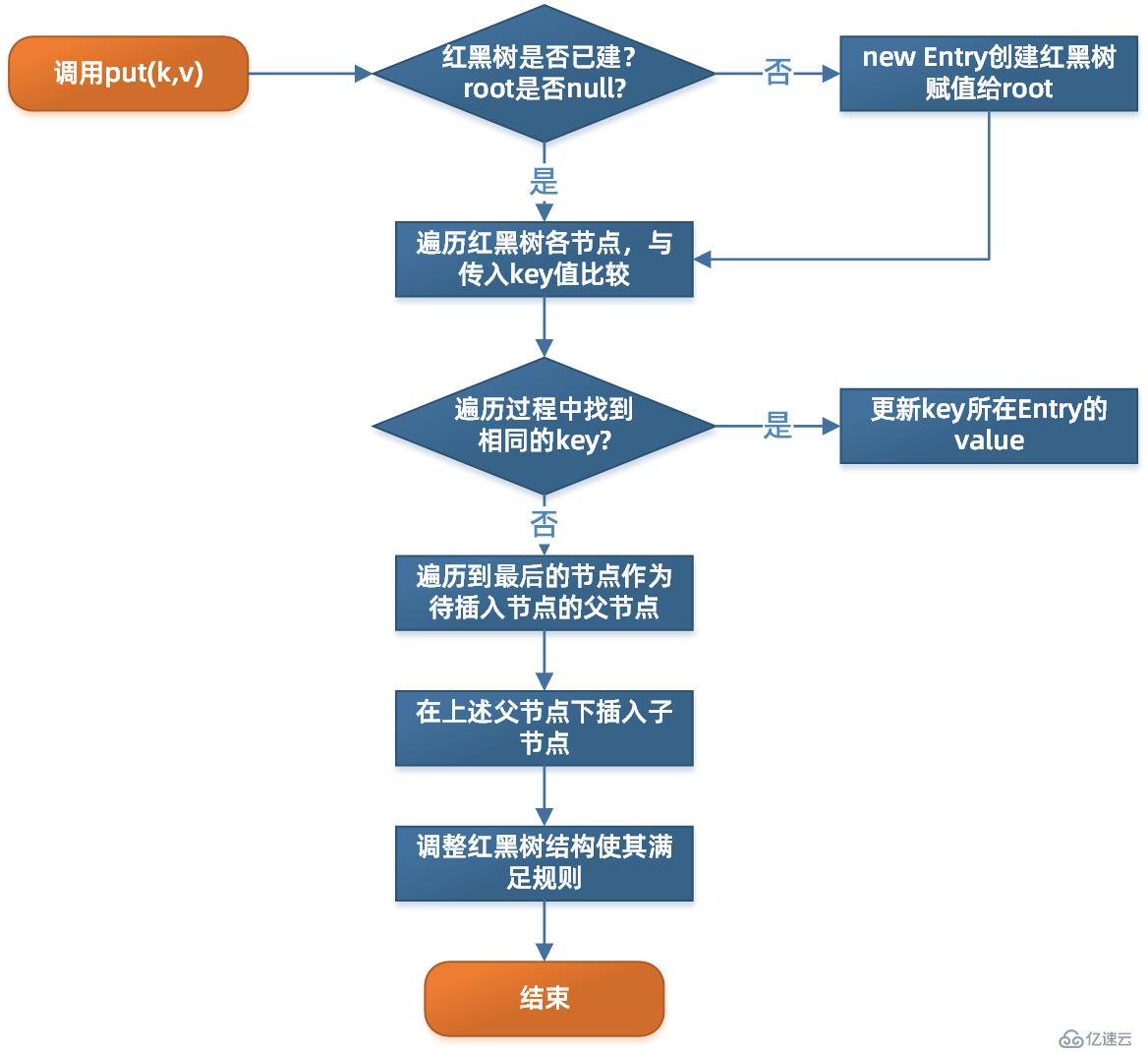
我們來分析一下源碼
public V put(K key, V value) {
Entry<K,V> t = root;
/**
* 如果根節點都為null,還沒建立起來紅黑樹,我們先new Entry并賦值給root把紅黑樹建立起來,這個時候紅
* 黑樹中已經有一個節點了,同時修改操作+1。
*/
if (t == null) {
compare(key, key);
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
/**
* 如果節點不為null,定義一個cmp,這個變量用來進行二分查找時的比較;定義parent,是new Entry時必須
* 要的參數
*/
int cmp;
Entry<K,V> parent;
// cpr表示有無自己定義的排序規則,分兩種情況遍歷執行
Comparator<? super K> cpr = comparator;
if (cpr != null) {
/**
* 從root節點開始遍歷,通過二分查找逐步向下找
* 第一次循環:從根節點開始,這個時候parent就是根節點,然后通過自定義的排序算法
* cpr.compare(key, t.key)比較傳入的key和根節點的key值,如果傳入的key<root.key,那么
* 繼續在root的左子樹中找,從root的左孩子節點(root.left)開始:如果傳入的key>root.key,
* 那么繼續在root的右子樹中找,從root的右孩子節點(root.right)開始;如果恰好key==root.key,
* 那么直接根據root節點的value值即可。
* 后面的循環規則一樣,當遍歷到的當前節點作為起始節點,逐步往下找
*
* 需要注意的是:這里并沒有對key是否為null進行判斷,建議自己的實現Comparator時應該要考慮在內
*/
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
//從這里看出,當默認排序時,key值是不能為null的
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
//這里的實現邏輯和上面一樣,都是通過二分查找,就不再多說了
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
/**
* 能執行到這里,說明前面并沒有找到相同的key,節點已經遍歷到最后了,我們只需要new一個Entry放到
* parent下面即可,但放到左子節點上還是右子節點上,就需要按照紅黑樹的規則來。
*/
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e;
else
parent.right = e;
/**
* 節點加進去了,并不算完,我們在前面紅黑樹原理章節提到過,一般情況下加入節點都會對紅黑樹的結構造成
* 破壞,我們需要通過一些操作來進行自動平衡處置,如【變色】【左旋】【右旋】
*/
fixAfterInsertion(e);
size++;
modCount++;
return null;
}put方法源碼中通過fixAfterInsertion(e)方法來進行自平衡處理,我們回顧一下插入時自平衡調整的邏輯
| 無需調整 | 【變色】即可實現平衡 | 【旋轉+變色】才可實現平衡 | |
|---|---|---|---|
| 情況1: | 當父節點為黑色時插入子節點 | 空樹插入根節點,將根節點紅色變為黑色 | 父節點為紅色左節點,叔父節點為黑色,插入左子節點,那么通過【左左節點旋轉】 |
| 情況2: | - | 父節點和叔父節點都為紅色 | 父節點為紅色左節點,叔父節點為黑色,插入右子節點,那么通過【左右節點旋轉】 |
| 情況3: | - | - | 父節點為紅色右節點,叔父節點為黑色,插入左子節點,那么通過【右左節點旋轉】 |
| 情況4: | - | - | 父節點為紅色右節點,叔父節點為黑色,插入右子節點,那么通過【右右節點旋轉】 |
接下來我們看一看這個方法
private void fixAfterInsertion(Entry<K,V> x) {
//新插入的節點為紅色節點
x.color = RED;
//我們知道父節點為黑色時,并不需要進行樹結構調整,只有當父節點為紅色時,才需要調整
while (x != null && x != root && x.parent.color == RED) {
//如果父節點是左節點,對應上表中情況1和情況2
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
//如果叔父節點為紅色,對應于“父節點和叔父節點都為紅色”,此時通過變色即可實現平衡
//此時父節點和叔父節點都設置為黑色,祖父節點設置為紅色
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
//如果插入節點是黑色,插入的是右子節點,通過【左右節點旋轉】(這里先進行父節點左旋)
if (x == rightOf(parentOf(x))) {
x = parentOf(x);
rotateLeft(x);
}
//設置父節點和祖父節點顏色
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
//進行祖父節點右旋(這里【變色】和【旋轉】并沒有嚴格的先后順序,達成目的就行)
rotateRight(parentOf(parentOf(x)));
}
} else {
//父節點是右節點的情況
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
//對應于“父節點和叔父節點都為紅色”,此時通過變色即可實現平衡
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
//如果插入節點是黑色,插入的是左子節點,通過【右左節點旋轉】(這里先進行父節點右旋)
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
//進行祖父節點左旋(這里【變色】和【旋轉】并沒有嚴格的先后順序,達成目的就行)
rotateLeft(parentOf(parentOf(x)));
}
}
}
//根節點必須為黑色
root.color = BLACK;
}源碼中通過 rotateLeft 進行【左旋】,通過 rotateRight 進行【右旋】。都非常類似,我們就看一下【左旋】的代碼,【左旋】規則如下:“逆時針旋轉兩個節點,讓一個節點被其右子節點取代,而該節點成為右子節點的左子節點”。
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
/**
* 斷開當前節點p與其右子節點的關聯,重新將節點p的右子節點的地址指向節點p的右子節點的左子節點
* 這個時候節點r沒有父節點
*/
Entry<K,V> r = p.right;
p.right = r.left;
//將節點p作為節點r的父節點
if (r.left != null)
r.left.parent = p;
//將節點p的父節點和r的父節點指向同一處
r.parent = p.parent;
//p的父節點為null,則將節點r設置為root
if (p.parent == null)
root = r;
//如果節點p是左子節點,則將該左子節點替換為節點r
else if (p.parent.left == p)
p.parent.left = r;
//如果節點p為右子節點,則將該右子節點替換為節點r
else
p.parent.right = r;
//重新建立p與r的關系
r.left = p;
p.parent = r;
}
}就算是看了上面的注釋還是并不清晰,看下圖你就懂了

get方法是通過二分查找的思想,我們看一下源碼
public V get(Object key) {
Entry<K,V> p = getEntry(key);
return (p==null ? null : p.value);
}
/**
* 從root節點開始遍歷,通過二分查找逐步向下找
* 第一次循環:從根節點開始,這個時候parent就是根節點,然后通過k.compareTo(p.key)比較傳入的key和
* 根節點的key值;
* 如果傳入的key<root.key, 那么繼續在root的左子樹中找,從root的左孩子節點(root.left)開始;
* 如果傳入的key>root.key, 那么繼續在root的右子樹中找,從root的右孩子節點(root.right)開始;
* 如果恰好key==root.key,那么直接根據root節點的value值即可。
* 后面的循環規則一樣,當遍歷到的當前節點作為起始節點,逐步往下找
*/
//默認排序情況下的查找
final Entry<K,V> getEntry(Object key) {
if (comparator != null)
return getEntryUsingComparator(key);
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
return null;
}
/**
* 從root節點開始遍歷,通過二分查找逐步向下找
* 第一次循環:從根節點開始,這個時候parent就是根節點,然后通過自定義的排序算法
* cpr.compare(key, t.key)比較傳入的key和根節點的key值,如果傳入的key<root.key,那么
* 繼續在root的左子樹中找,從root的左孩子節點(root.left)開始:如果傳入的key>root.key,
* 那么繼續在root的右子樹中找,從root的右孩子節點(root.right)開始;如果恰好key==root.key,
* 那么直接根據root節點的value值即可。
* 后面的循環規則一樣,當遍歷到的當前節點作為起始節點,逐步往下找
*/
//自定義排序規則下的查找
final Entry<K,V> getEntryUsingComparator(Object key) {
@SuppressWarnings("unchecked")
K k = (K) key;
Comparator<? super K> cpr = comparator;
if (cpr != null) {
Entry<K,V> p = root;
while (p != null) {
int cmp = cpr.compare(k, p.key);
if (cmp < 0)
p = p.left;
else if (cmp > 0)
p = p.right;
else
return p;
}
}
return null;
}remove方法可以分為兩個步驟,先是找到這個節點,直接調用了上面介紹的getEntry(Object key),這個步驟我們就不說了,直接說第二個步驟,找到后的刪除操作。
public V remove(Object key) {
Entry<K,V> p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
deleteEntry(p);
return oldValue;
}通過deleteEntry(p)進行刪除操作,刪除操作的原理我們在前面已經講過
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
//當左右子節點都不為null時,通過successor(p)遍歷紅黑樹找到前驅或者后繼
if (p.left != null && p.right != null) {
Entry<K,V> s = successor(p);
//將前驅或者后繼的key和value復制到當前節點p中,然后刪除節點s(通過將節點p引用指向s)
p.key = s.key;
p.value = s.value;
p = s;
}
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
/**
* 至少有一個子節點不為null,直接用這個有值的節點替換掉當前節點,給replacement的parent屬性賦值,給
* parent節點的left屬性和right屬性賦值,同時要記住葉子節點必須為null,然后用fixAfterDeletion方法
* 進行自平衡處理
*/
if (replacement != null) {
//將待刪除節點的子節點掛到待刪除節點的父節點上。
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
/**
* p如果是紅色節點的話,那么其子節點replacement必然為紅色的,并不影響紅黑樹的結構
* 但如果p為黑色節點的話,那么其父節點以及子節點都可能是紅色的,那么很明顯可能會存在紅色相連的情
* 況,因此需要進行自平衡的調整
*/
if (p.color == BLACK)
fixAfterDeletion(replacement);
} else if (p.parent == null) {//這種情況就不用多說了吧
root = null;
} else {
/**
* 如果p節點為黑色,那么p節點刪除后,就可能違背每個節點到其葉子節點路徑上黑色節點數量一致的規則,
* 因此需要進行自平衡的調整
*/
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}操作的操作其實很簡單,場景也不多,我們看一下刪除后的自平衡操作方法fixAfterDeletion
private void fixAfterDeletion(Entry<K,V> x) {
/**
* 當x不是root節點且顏色為黑色時
*/
while (x != root && colorOf(x) == BLACK) {
/**
* 首先分為兩種情況,當前節點x是左節點或者當前節點x是右節點,這兩種情況下面都是四種場景,這里通過
* 代碼分析一下x為左節點的情況,右節點可參考左節點理解,因為它們非常類似
*/
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
/**
* 場景1:當x是左黑色節點,兄弟節點sib是紅色節點
* 兄弟節點由紅轉黑,父節點由黑轉紅,按父節點左旋,
* 左旋后樹的結構變化了,這時重新賦值sib,這個時候sib指向了x的兄弟節點
*/
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
sib = rightOf(parentOf(x));
}
/**
* 場景2:節點x、x的兄弟節點sib、sib的左子節點和右子節點都為黑色時,需要將該節點sib由黑變
* 紅,同時將x指向當前x的父節點
*/
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
/**
* 場景3:節點x、x的兄弟節點sib、sib的右子節點都為黑色,sib的左子節點為紅色時,
* 需要將sib左子節點設置為黑色,sib節點設置為紅色,同時按sib右旋,再將sib指向x的
* 兄弟節點
*/
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK);
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
/**
* 場景4:節點x、x的兄弟節點sib都為黑色,而sib的左右子節點都為紅色或者右子節點為紅色、
* 左子節點為黑色,此時需要將sib節點的顏色設置成和x的父節點p相同的顏色,
* 設置x的父節點為黑色,設置sib右子節點為黑色,左旋x的父節點p,然后將x賦值為root
*/
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else {//x是右節點的情況
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}當待操作節點為左節點時,上面描述了四種場景,而且場景之間可以相互轉換,如deleteEntry后進入了場景1,經過場景1的一些列操作后,紅黑樹的結構并沒有調整完成,而是進入了場景2,場景2執行完成后跳出循環,將待操作節點設置為黑色,完成。我們下面用圖來說明一下四種場景幫助理解,當然大家最好自己手動畫一下。
場景1:
當x是左黑色節點,兄弟節點sib是紅色節點,需要兄弟節點由紅轉黑,父節點由黑轉紅,按父節點左旋,左旋后樹的結構變化了,這時重新賦值sib,這個時候sib指向了x的兄弟節點。

但經過這一系列操作后,并沒有結束,而是可能到了場景2,或者場景3和4
場景2:
節點x、x的兄弟節點sib、sib的左子節點和右子節點都為黑色時,需要將該節點sib由黑變紅,同時將x指向當前x的父節點
經過場景2的一系列操作后,循環就結束了,我們跳出循環,將節點x設置為黑色,自平衡調整完成。
場景3:
節點x、x的兄弟節點sib、sib的右子節點都為黑色,sib的左子節點為紅色時,需要將sib左子節點設置為黑色,sib節點設置為紅色,同時按sib右旋,再將sib指向x的兄弟節點
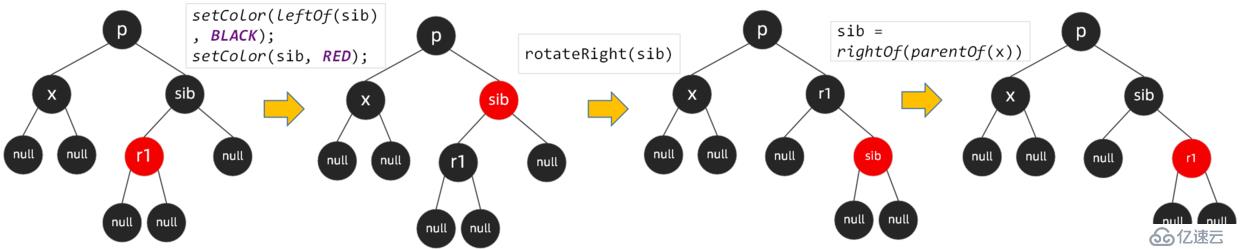
并沒有完,場景3的一系列操作后,會進入到場景4
場景4:
節點x、x的兄弟節點sib都為黑色,而sib的左右子節點都為紅色或者右子節點為紅色、左子節點為黑色,此時需要將sib節點的顏色設置成和x的父節點p相同的顏色,設置x的父節點顏色為黑色,設置sib右孩子的顏色為黑色,左旋x的父節點p,然后將x賦值為root
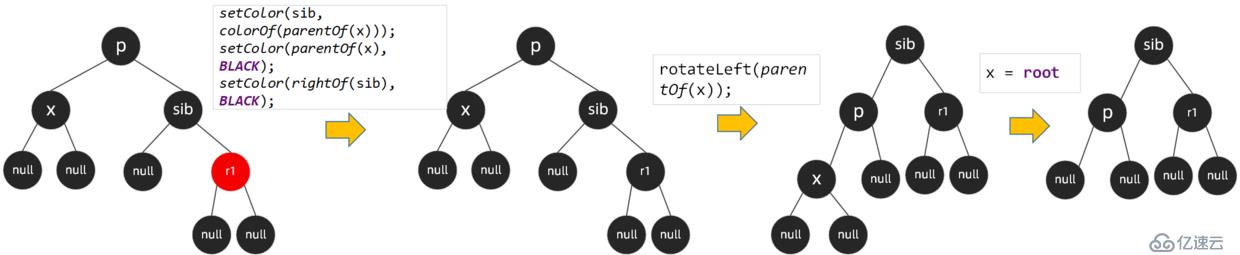
四種場景講完了,刪除后的自平衡操作不太好理解,代碼層面的已經弄明白了,但如果讓我自己去實現的話,還是差了一些,還需要再研究。
遍歷比較簡單,TreeMap的遍歷可以使用map.values(), map.keySet(),map.entrySet(),map.forEach(),這里不再多說。
本文詳細介紹了TreeMap的基本特點,并對其底層數據結構紅黑樹進行了回顧,同時講述了其自動排序的原理,并從源碼的角度結合紅黑樹圖形對put方法、get方法、remove方法進行了講解,最后簡單提了一下遍歷操作,若有不對之處,請批評指正,望共同進步,謝謝!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。