您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇文章給大家分享的是有關如何進行TreeMap源碼解析,小編覺得挺實用的,因此分享給大家學習,希望大家閱讀完這篇文章后可以有所收獲,話不多說,跟著小編一起來看看吧。
今天我們來學習一種新的集合叫做TreeMap。TreeMap底層并不是通過哈希表的方式實現的,而是采用了一種全新的數據結構,紅黑樹結構存儲的。下面我們簡單介紹一下紅黑樹的相關知識。
紅黑樹的基本概念
紅黑樹也叫紅黑二叉樹,所以它也是二叉樹的一種,除了具有二叉樹的基本特性外,還有自己獨特的一些特性。二叉樹也就是說在每個樹節點最多有兩個子節點的樹結構。并且二叉樹的子節點有左右之分,且左節點的值都要小于右節點的。所以,通過二叉樹結構存儲的數據在檢索元素時速度會很快,因為從樹根節點檢索時,就會過濾掉將近一半的數據(理想情況下)。并且紅黑樹是一種平衡二叉樹,這也是紅黑樹的一種特性。下面我們來看一下什么是平衡二叉樹。
紅黑樹特性
平衡二叉樹主要具有以下特性:它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1,并且左右兩個子樹也都是一棵平衡二叉樹。說白了紅黑樹就是平衡二叉樹的一種實現算法,除此算法外還有AVL、Treap、伸展樹、SBT等算法。(主要來源為百度百科)
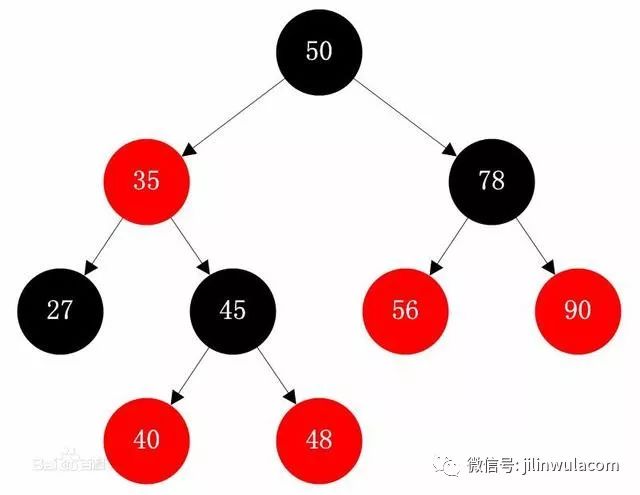
下面我們繼續介紹紅黑樹的其它特性,紅黑樹顧名思義就是通過設置紅色或黑色等狀態來保證樹的平衡的。所以紅黑樹的主要特性如下:
每個節點只能是紅色,或黑色
根節點必須是黑色
每個葉節點(NIL或NULL)是黑色
如果一個節點是紅色的,則它的子節點必須是黑色(全部節點)
從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點
紅黑樹的旋轉
上面是紅黑樹的相關特性,也就是說無論任何時候紅黑樹都必須保證具有上面的全部特性。但是在我們日常開發時,常常需要向集合中添加或者刪除元素,那么在執行上述操作時,難免會破壞紅黑樹的相關特性,那么這時應該怎么處理呢?事實上,每當我們執行添加或者刪除操作時,如果破壞了紅黑樹的特性,那么這時就會進行樹的旋轉,以保證紅黑樹的相關特性。紅黑樹的旋轉主要分為左旋和右旋。下面我們分別看看具體的實現。
左旋
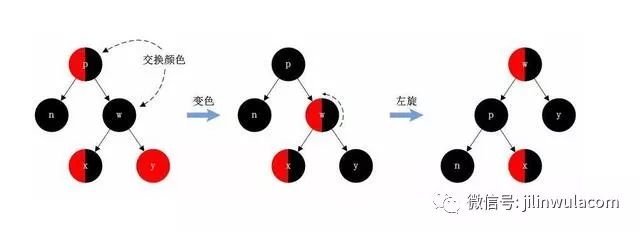
紅黑樹進行左旋的邏輯是,將要左旋的節點的父節點設置為自己的左節點,然后將原左節點設置為新左節點的右節點。
右旋
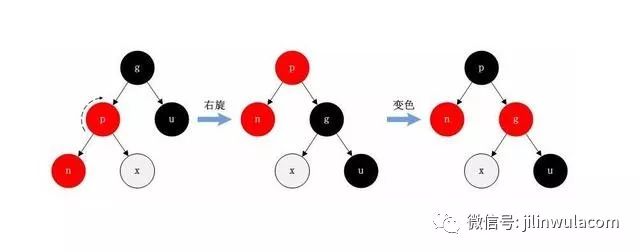
紅黑樹進行右旋的邏輯是,將要右旋的節點的父節點設置為自己的右節點,然后將原右節點設置為新右節點的左節點。
現在我們已經知道了有關紅黑樹的所有知識,下面我們分析一下TreeMap的底層源碼,看TreeMap底層是怎么實現紅黑樹的邏輯的。我們還是和其它集合一樣還是先看TreeMap的初始化。

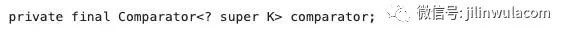
上面是TreeMap的無參構造函數,我們發現當我們通過參構造函數創建TreeMap對象時,并不會執行底層樹結構的初始化,而只是將comparator設置為空。那么通過我們以往分析其它集合時總結的規律,TreeMap的初始化一定是在第一次調用put方法時執行的。下面我們將重點看一下TreeMap中的put方法。





下面我們看一下上述方法中提到的fixAfterInsertion方法的具體邏輯也就是左旋和右旋的具體實現。



左旋和右旋的具體邏輯這里就不在詳細分析了,主要的實現邏輯就是上面所說的,左旋就是講要左旋的節點的父節點設置為自己的左節點,然后將原左節點設置為新左節點的右節點。右旋就是講右旋的的父節點設置為自己的右節點,然后將原右節點設置為新右節點的左節點。
總結
在TreeMap中不允許用null做為key保存到TreeMap集合中
我們在分析源碼時并沒有發現同步關鍵字synchronized,這就說明TreeMap也不是一個線程安全的集合類
我們在分析源碼時知道TreeMap每次都添加元素時都會進行key的比較,所以我們在使用TreeMap集合是必須保證存儲在TreeMap中的元素是可以比較的,否則虛擬機會直接拋出一場。例如


以上就是如何進行TreeMap源碼解析,小編相信有部分知識點可能是我們日常工作會見到或用到的。希望你能通過這篇文章學到更多知識。更多詳情敬請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。