您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
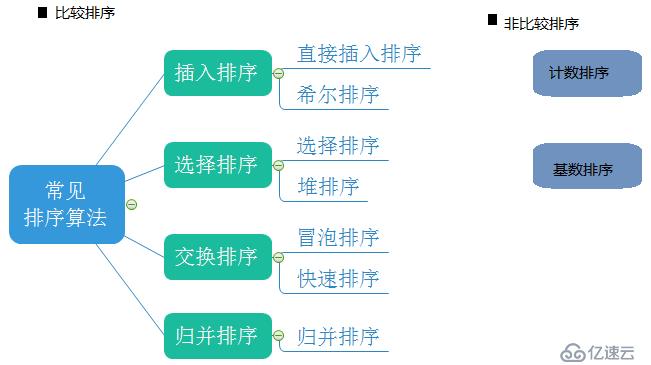
數據結構中的排序算法分為比較排序,非比較排序。比較排序有插入排序、選擇排序、交換排序、歸并排序,非比較排序有計數排序、基數排序。下面是排序的具體分類:
1.直接排序
主要思想:使用兩個指針,讓一個指針從開始,另一個指針指向前一個指針的+1位置,兩個數據進行比較
void InsertSort(int* a, size_t size)
{
assert(a);
for (size_t i = 0; i < size - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0 && a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
a[end + 1] = tmp; //當進行到a[end]>tmp的時候,將tmp插入到a[end+1]的位置上
}
}2.希爾排序
主要思想:給定間距gap,將間距上的數據進行排序,然后將間距進行縮小,當間距為1時,就相當于進行直接插入排序,這就避免了,直接排序有序的情況,提高排序的效率
void shellSort(int* a, size_t size)
{
assert(a);
int gap = size;
while (gap > 1) //當gap為2或者1時,進入循環中gap = 1,相當于進行直接插入排序
{
gap = gap / 3 + 1;
for (size_t i = 0; i < size - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0 && a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
a[end + gap] = tmp;
}
}
}3.選擇排序
主要思想: 每一次從所要排序的數據中選出最大的數據,放入到數組的最后位置上,用數組的下標來控制放置的位置,直到排好順序
void selectSort(int* a, size_t size)
{
assert(a);
for (size_t i = 0; i < size - 1; i++)
{
int max = a[0];
int num = 0;
for (size_t j = 0; j < size - i; j++)
{
if (max < a[j])
{
max = a[j];
num = j;
}
}
swap(a[num], a[size - i - 1]);
}
}選擇排序優化后的思想:每一次可以選兩個數據,最大數據和最小數據,將最大數據從數組的最大位置開始放置,最小數據從數組的最小位置開始放置,能夠提高排序的效率
void selectSort(int* a, size_t size)
{
int left = 0;
int right = size - 1;
while (left < right)
{
for (int i = left; i < right; i++)
{
int min = a[left];
int max = a[right];
if (a[i] < min)
{
min = a[i];
swap(a[i], a[left]);
}
if (a[i] > max)
{
max = a[i];
swap(a[i], a[right]);
}
}
++left;
--right;
}
}4.堆排序
主要思想:創建一個大堆進行排序,堆排序只能排序數組,通過數組的下表來計算數據在堆中的位置,將大堆的根節點與最后一個葉子節點進行交換,然后對堆中剩下的數據進行調整,直到再次成為大堆。
void AdjustDown(int* a, size_t root, size_t size)
{
assert(a);
size_t parent = root;
size_t child = parent * 2 + 1;
while (child < size)
{
if (child + 1 < size && a[child + 1] > a[child])
{
++child;
}
if (a[child] > a[parent])
{
swap(a[child], a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, size_t size)
{
for (int i = (size - 2) / 2; i >= 0; --i)
//從最后一個父親節點開始建堆(使用i>=0時,必須使用int類型)
{
AdjustDown(a, i, size);
}
for (size_t i = 0; i < size; i++) //進行排序,最大的數往下放
{
swap(a[0], a[size - i - 1]);
AdjustDown(a, 0, size - i - 1);
}
}5.快速排序
方法一:
主要思想:先選定一個key值(一般是數組的頭元素或者尾元素),這里選定數組的尾元素,給定兩個指針begin和end,begin指針指向數組的頭位置,end指針指向倒數第二個位置,begin指針找比key值大的數據,end指針找較key值小的數據,如果begin指針還沒有和end相遇,則將a[begin]和a[end]數據進行交換。當begin和end指針相遇,則將key值和a[begin]進行交換。
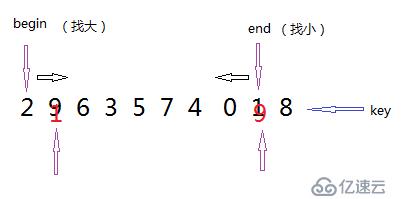
int partSort(int* a, int left, int right)
{
assert(a);
int key = a[right]; //選最右端的數據作為key
int begin = left;
int end = right - 1;
while (begin < end)
{
while (begin < end && a[begin] <= key) //begin找比key大的數據
{
++begin;
}
while (begin < end && a[end] >= key) //end找比key小的數據
{
--end;
}
if (begin < end)
{
swap(a[begin], a[end]);
}
}
if (a[begin] > a[right]) //只有兩個元素的情況
{
swap(a[begin], a[right]);
return begin;
}
else
{
return right;
}
return begin;
}
void QuickSort(int* a, int left, int right)
{
assert(a);
if (left >= right)
{
return;
}
int point = partSort(a, left, right);
QuickSort(a, left, point-1);
QuickSort(a, point+1, right);
}方法二:
主要思想:挖坑法實現,將最右邊的數據用key進行保存,可以說這時候最后的位置相當于一個坑,能夠對數據進行任意的更改,將左指針找到的較key值大的數據賦值到key的位置上,這時候左指針指向的位置可以形成一個坑,這時再用右指針找較key值小的數據,將其賦值到剛才的坑中,這時右指針指向的位置也就行成坑。最后當兩個指針相遇時,將key值賦值到坑中,這時左邊的數據都小于key值,右邊的數據都大于key值。
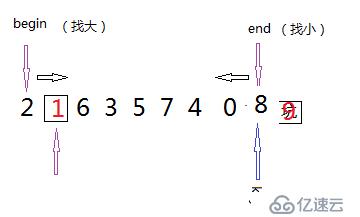
其中,若選取數組中最大或者最小的數據為key值,這是快速排序的最壞情況,利用三數取中的方法可以解決這種問題,取數組中頭元素、尾元素、和中間元素的最中間大小的數據作為key值,就能夠避免這樣的情況。
//三數取中法
int GetMidIndex(int* a, int left, int right)
{
assert(a);
int mid = (left + right) / 2;
if (a[left] < a[right])
{
if (a[mid] < a[left]) //a[mid] < a[left] < a[right]
{
return left;
}
else if (a[mid] > a[right]) //a[left] < a[right] < a[mid]
{
return right;
}
else //a[left] < a[mid] < a[right]
{
return mid;
}
}
else
{
if (a[mid] < a[right]) //a[left] > a[right] > a[mid]
{
return right;
}
else if (a[mid] > a[left]) //a[right] < a[left] < a[mid]
{
return left;
}
else //a[right] < a[mid] < a[left]
{
return mid;
}
}
}
int partSort1(int* a, int left, int right)
{
int index = GetMidIndex(a, left, right);
swap(a[index], a[right]); //將中間的數據與最右邊的數據進行交換,然后將最右邊數據賦值給key
int key = a[right]; //首先將最右邊的位置作為第一個坑
int begin = left;
int end = right;
while (begin < end)
{
while (begin < end && a[begin] <= key) //從左往右找較key大的數據
{
++begin;
}
a[end] = a[begin]; //將第一個坑進行覆蓋,同時空出新的坑
while (begin < end && a[end] >= key) //從右往左查找較key小的數據
{
--end;
}
a[begin] = a[end]; //將第二個坑進行覆蓋,同時空出新的坑
}
if (begin == end)
{
a[end] = key; //key現在的位置,左邊的數據都較key值小,右邊的數據豆角key值大
return begin;
}
}
void QuickSort1(int* a, int left, int right)
{
assert(a);
if (left > right)
{
return;
}
int ret = partSort1(a, left, right);
QuickSort1(a, left, ret - 1);
QuickSort1(a, ret + 1, right);
}方法三:
主要思想:選定最右邊的數據為key,將cur指針指向數組的頭元素,cur指針找較key值小的數據,prev指針指向cur-1的位置,當cur找到較小的數據,先進行prev++,若此時cur=prev,cur繼續找較小的數據,直到cur!=prev,就將a[prev]和a[cur]進行交換,直到cur指向數組的倒數第二個元素,這時將key值和a[++prev]進行交換。
int partSort2(int* a, int left, int right)
{
int key = a[right];
int cur = left;
int prev = left - 1;
while (cur < right)
{
if (a[cur] < key && ++prev != cur)
{
swap(a[cur], a[prev]);
}
++cur;
}
swap(a[right], a[++prev]);
return prev;
}
void QuickSort2(int* a, int left, int right)
{
assert(a);
if (left > right)
{
return;
}
int ret = partSort2(a, left, right);
QuickSort2(a, left, ret - 1);
QuickSort2(a, ret + 1, right);
} 優化:當區間gap<13,采用直接排序效率會高于都采用快速排序,能夠減少程序壓棧的開銷
//核心代碼
void QuickSort1(int* a, int left, int right)
{
assert(a);
if (left > right)
{
return;
}
int gap = right - left + 1;
if (gap < 13)
{
InsertSort(a, gap);
}
int ret = partSort1(a, left, right);
QuickSort1(a, left, ret - 1);
QuickSort1(a, ret + 1, right);
}
——如果不使用遞歸,那應該怎樣實現快速排序算法呢?(利用棧進行保存左邊界和右邊界)
//核心代碼
void QuickSort_NonR(int* a, int left, int right)
{
assert(a);
stack<int> s;
if (left < right) //當left < right證明需要排序的數據大于1
{
s.push(right);
s.push(left);
}
while (!s.empty())
{
left = s.top();
s.pop();
right = s.top();
s.pop();
if (right - left < 13)
{
InsertSort(a, right - left + 1);
}
else
{
int div = partSort1(a, left, right);
if (left < div - 1)
{
s.push(div - 1);
s.push(left);
}
if (div + 1 < right)
{
s.push(right);
s.push(div + 1);
}
}
}
}6.歸并排序
主要思想:與合并兩個有序數組算法相似,需要借助一塊O(N)的空間,將一個數組中的元素分為兩部分,若這兩個部分都能夠有序,則利用合并的思想進行合并,過程一直進行遞歸
void _Merge(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{
int index = begin1; //用來標記tmp數組的下標
while (begin1 <= end1 && begin2 <= end2)
//先判斷begin1和begin2的大小,然后將小的數據從begin到end拷貝到tmp上,
//出循環的條件begin1>=end1 || begin2 >= end2
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
//將剩下的begin1或者begin2在進行拷貝
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
void _MergeSort(int* a, int* tmp, int left, int right)
{
if (left < right)
{
int mid = (right + left) / 2;
_MergeSort(a, tmp, left, mid);
_MergeSort(a, tmp, mid + 1, right);
_Merge(a, tmp, left, mid, mid + 1, right); //借助tmp進行排序
//將tmp上面排序后的數據再拷貝到上層的數組中
for (int i = left; i <= right; ++i)
{
a[i] = tmp[i];
}
}
}
void MergeSort(int* a, int size) //歸并排序數組
{
assert(a);
int* tmp = new int[size]; //開辟N個空間
int left = 0;
int right = size - 1;
_MergeSort(a, tmp, left, right);
delete[] tmp;
} 上面主要介紹的為各個比較排序的算法實現,非比較排序(計數、基數)在下篇:“數據結構—各類‘排序算法’實現(下)”
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。