您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇“Java順序表和鏈表如何實現”文章的知識點大部分人都不太理解,所以小編給大家總結了以下內容,內容詳細,步驟清晰,具有一定的借鑒價值,希望大家閱讀完這篇文章能有所收獲,下面我們一起來看看這篇“Java順序表和鏈表如何實現”文章吧。
線性表(linear list)是n個具有相同特性的數據元素的有限序列。 線性表是一種在實際中廣泛使用的數據結構,常見的線性表:順序表、鏈表、棧、隊列、字符串…
線性表在邏輯上是線性結構,也就說是連續的一條直線。但是在物理結構上并不一定是連續的,線性表在物理上存儲時,通常以數組和鏈式結構的形式存儲。
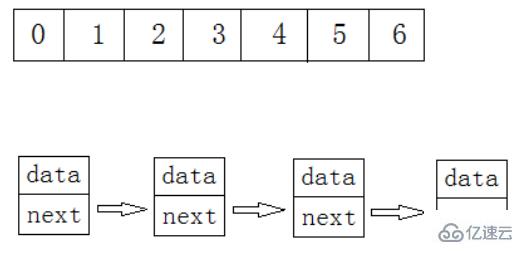
其實就是一個數組。【增刪查改】那為什么還有寫一個順序表,直接用數組就好了嘛?不一樣,寫到類里面 將來就可以 面向對象了。
順序表是用一段物理地址連續的存儲單元依次存儲數據元素的線性結構,一般情況下采用數組存儲。在數組上完成數據的增刪查改。
順序表一般可以分為:
靜態順序表:使用定長數組存儲。
動態順序表:使用動態開辟的數組存儲。
靜態順序表適用于確定知道需要存多少數據的場景.
靜態順序表的定長數組導致N定大了,空間開多了浪費,開少了不夠用.
相比之下動態順序表更靈活, 根據需要動態的分配空間大小.
我們來實現一個動態順序表. 以下是需要支持的接口.

這里我們挨個拆解出來:
這是我們順序表的基本結構。下面我們就把順序表的功能一個一個拆解出來:public class MyArrayList {
public int[] elem;
public int usedSize;//有效的數據個數
public MyArrayList() {
this.elem = new int[10];
}
// 打印順序表public void display() {
}
System.out.println();}// 獲取順序表長度public int size() {
return 0;}// 在 pos 位置新增元素public void add(int pos, int data) {}// 判定是否包含某個元素public boolean contains(int toFind) {
return true;}// 查找某個元素對應的位置public int search(int toFind) {
return -1;}// 獲取 pos 位置的元素public int getPos(int pos) {
return -1;}// 給 pos 位置的元素設為 valuepublic void setPos(int pos, int value) {}//刪除第一次出現的關鍵字keypublic void remove(int toRemove) {}// 清空順序表public void clear() {}}
打印數據表:
獲取順序表長度: 在 pos 位置新增元素: 判斷是否包含某個元素: 查找某個元素對應的位置: 獲取 pos 位置的元素: 給 pos 位置的元素設為 value: 刪除第一次出現的關鍵字key: 清空順序表:public void display() {
for (int i = 0; i < this.usedSize; i++) {
System.out.print(this.elem[i] + " ");
}
System.out.println();}public int size() {
return this.usedSize;}public void add(int pos, int data) {
if(pos < 0 || pos > this.usedSize) {
System.out.println("pos 位置不合法");
return;
}
if(isFull()){
this.elem = Arrays.copyOf(this.elem,2*this.elem.length);
}
for (int i = this.usedSize-1; i >= pos; i--) {
this.elem[i + 1] = this.elem[i];
}
this.elem[pos] = data;
this.usedSize++;}//判斷數組元素是否等于有效數據個數public boolean isFull() {
return this.usedSize == this.elem.length;}public boolean contains(int toFind) {
for (int i = 0; i < this.usedSize; i++) {
if (this.elem[i] == toFind) {
return true;
}
}
return false;}public int search(int toFind) {
for (int i = 0; i < this.usedSize; i++) {
if (this.elem[i] == toFind) {
return i;
}
}
return -1;}public int getPos(int pos) {
if (pos < 0 || pos >= this.usedSize){
System.out.println("pos 位置不合法");
return -1;//所以 這里說明一下,業務上的處理,這里不考慮
}
if(isEmpty()) {
System.out.println("順序表為空!");
return -1;
}
return this.elem[pos];}//判斷數組鏈表是否為空public boolean isEmpty() {
return this.usedSize == 0;}public void setPos(int pos, int value) {
if(pos < 0 || pos >= this.usedSize) {
System.out.println("pos 位置不合法");
return;
}
if(isEmpty()) {
System.out.println("順序表為空!");
return;
}
this.elem[pos] = value;}//判斷數組鏈表是否為空public boolean isEmpty() {
return this.usedSize == 0;}public void remove(int toRemove) {
if(isEmpty()) {
System.out.println("順序表為空!");
return;
}
int index = search(toRemove);//index記錄刪除元素的位置
if(index == -1) {
System.out.println("沒有你要刪除的數字!");
}
for (int i = index; i < this.usedSize - 1; i++) {
this.elem[i] = this.elem[i + 1];
}
this.usedSize--;
//this.elem[usedSize] = null;引用數組必須這樣做才可以刪除}public void clear() {
this.usedSize = 0;}
順序表中間/頭部的插入刪除,時間復雜度為O(N)
增容需要申請新空間,拷貝數據,釋放舊空間。會有不小的消耗。
增容一般是呈2倍的增長,勢必會有一定的空間浪費。例如當前容量為100,滿了以后增容到200,我們再繼續插入了5個數據,后面沒有數據插入了,那么就浪費了95個數據空間。
思考: 如何解決以上問題呢?下面給出了鏈表的結構來看看。
鏈表是一種物理存儲結構上非連續存儲結構,數據元素的邏輯順序是通過鏈表中的引用鏈接次序實現的 。
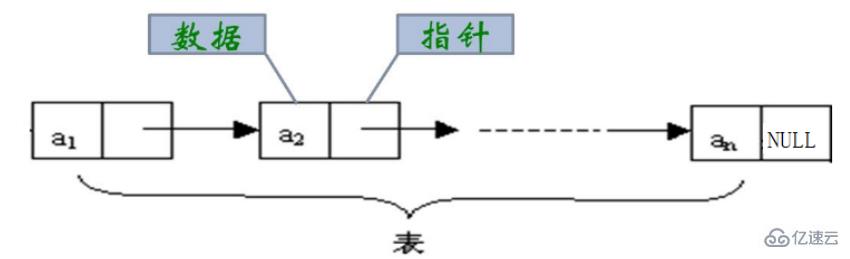
實際中鏈表的結構非常多樣,如果按一般來分的話就是四種:
單向鏈表
雙向鏈表
循環鏈表
雙向循環鏈表
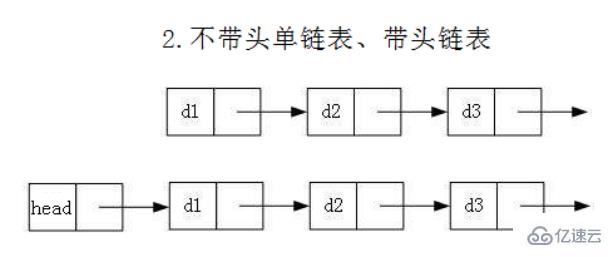
如果細分的話就有以下情況組合起來就有8種鏈表結構:
單向、雙向
帶頭、不帶頭
循環、非循環
這八種分別為:
單向 帶頭 循環
單向 不帶頭 循環
單向 帶頭 非循環
單向 不帶頭 非循環
雙向 帶頭 循環
雙向 不帶頭 循環
雙向 帶頭 非循環
雙向 不帶頭 非循環
注:上述加粗是我們重點需要學習的!!!

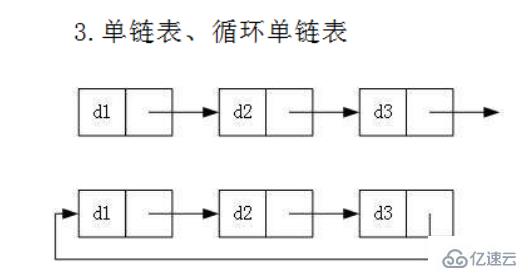
雖然有這么多的鏈表的結構,但是我們重點掌握兩種:
無頭單向非循環鏈表:結構簡單,一般不會單獨用來存數據。實際中更多是作為其他數據結構的子結構,如哈希桶、圖的鄰接表等等。另外這種結構在筆試面試中出現很多。
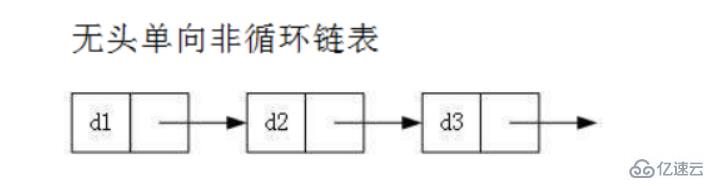
head:里面存儲的就是第一個節點(頭節點)的地址
head.next:存儲的就是下一個節點的地址
尾結點:它的next域是一個null
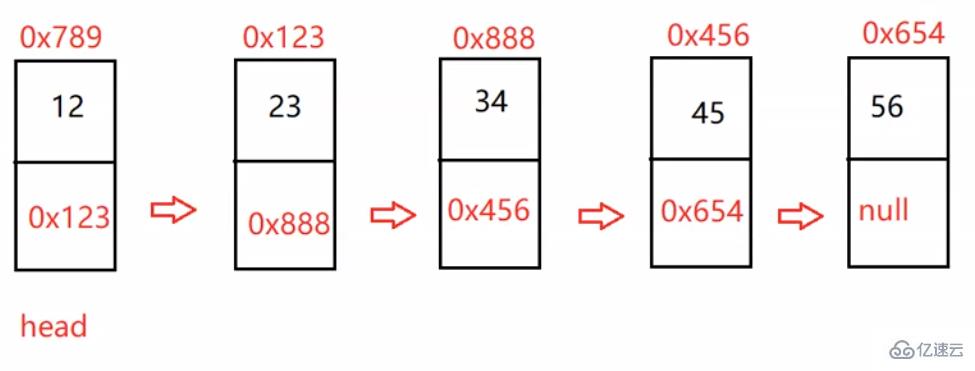
無頭雙向鏈表:在Java的集合框架庫中LinkedList底層實現就是無頭雙向循環鏈表。
最上面的數字是我們每一個數值自身的地址。
prev:指向前一個元素地址
next:下一個節點地址
data:數據
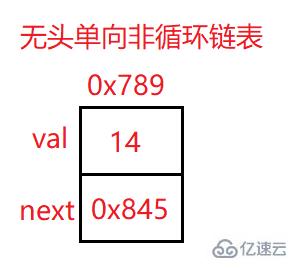
上面地址為改結點元素的地址
val:數據域
next:下一個結點的地址
head:里面存儲的就是第一個結點(頭結點)的地址
head.next:存儲的就是下一個結點的地址
無頭單向非循環鏈表實現:
上面是我們鏈表的初步結構(未給功能賦相關代碼,大家可以復制他們到自己的idea中進行練習,答案在下文中) 這里我們將他們一個一個拿出來實現 并實現!class ListNode {
public int val;
public ListNode next;//ListNode儲存的是結點類型
public ListNode (int val) {
this.val = val;
}}public class MyLinkedList {
public ListNode head;//鏈表的頭引用
public void creatList() {
ListNode listNode1 = new ListNode(12);
ListNode listNode2 = new ListNode(23);
ListNode listNode3 = new ListNode(34);
ListNode listNode4 = new ListNode(45);
ListNode listNode5 = new ListNode(56);
listNode1.next = listNode2;
listNode2.next = listNode3;
listNode3.next = listNode4;
listNode4.next = listNode5;
this.head = listNode1;
}
//查找是否包含關鍵字key是否在單鏈表當中
public boolean contains(int key) {
return true;
}
//得到單鏈表的長度
public int size(){
return -1;
}
//頭插法
public void addFirst(int data) {
}
//尾插法
public void addLast(int data) {
}
//任意位置插入,第一個數據節點為0號下標
public boolean addIndex(int index,int data) {
return true;
}
//刪除第一次出現關鍵字為key的節點
public void remove(int key) {
}
//刪除所有值為key的節點
public ListNode removeAllKey(int key) {
}
//打印鏈表中的所有元素
public void display() {
}
//清除鏈表中所有元素
public void clear() {
}}
打印鏈表中所有元素:
查找是否包含關鍵字key是否在單鏈表當中: 得到單鏈表的長度: 頭插法(一定要記住 綁定位置時一定要先綁定后面的數據 避免后面數據丟失): 尾插法: 任意位置插入,第一個數據結點為0號下標(插入到index后面一個位置):public void display() {
ListNode cur = this.head;
while(cur != null) {
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();}public boolean contains(int key) {
ListNode cur = this.head;
while (cur != null) {
if (cur.val == key) {
return true;
}
cur = cur.next;
}
return false;}public int size(){
int count = 0;
ListNode cur = this.head;
while (cur != null) {
count++;
cur = cur.next;
}
return count;}public void addFirst(int data) {
ListNode node = new ListNode(data);
node.next = this.head;
this.head = node;
/*if (this.head == null) {
this.head = node;
} else {
node.next = this.head;
this.head = node;
}*/}public void addLast(int data) {
ListNode node = new ListNode(data);
if (this.head == null) {
this.head = node;
} else {
ListNode cur = this.head;
while (cur.next != null) {
cur = cur.next;
}
cur.next = node;
}}
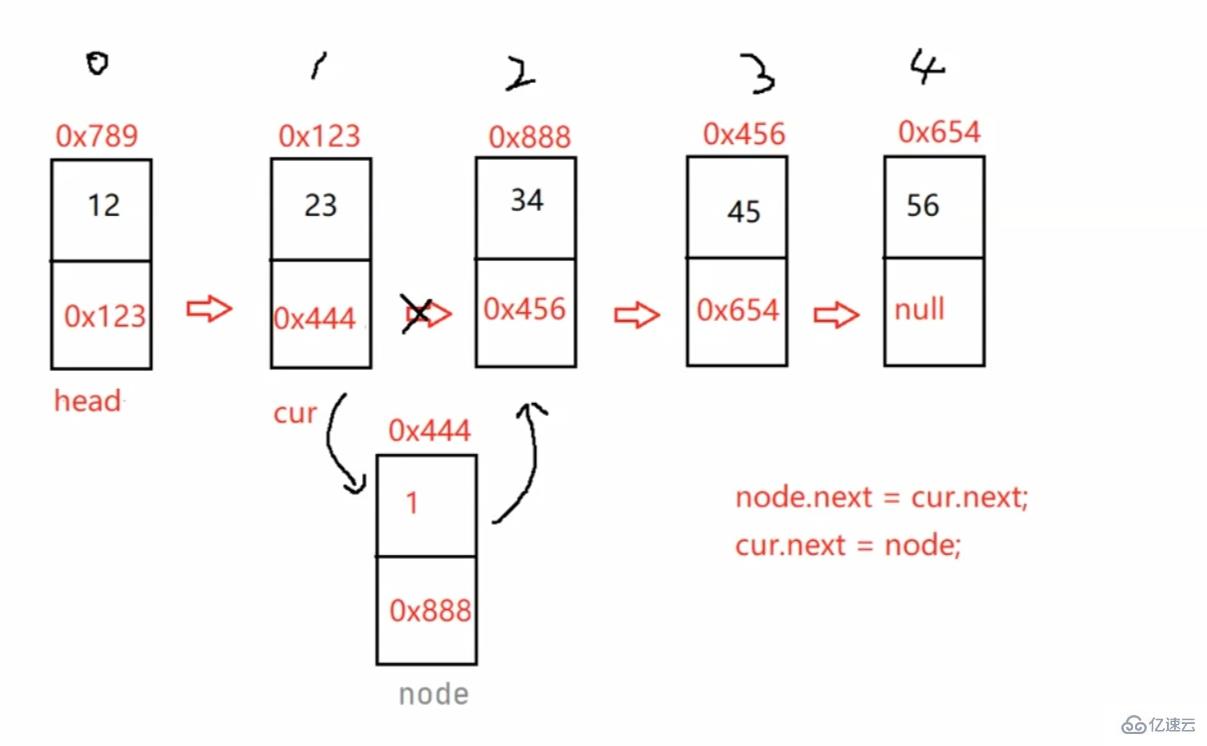
注意:單向鏈表找cur時要-1,但雙向鏈表不用 直接返回cur就好/**
* 找到index - 1位置的節點的地址
* @param index
* @return
*/public ListNode findIndex(int index) {
ListNode cur = this.head;
while (index - 1 != 0) {
cur = cur.next;
index--;
}
return cur;}//任意位置插入,第一個數據節點為0號下標public void addIndex(int index,int data) {
if(index < 0 || index > size()) {
System.out.println("index 位置不合法!");
return;
}
if(index == 0) {
addFirst(data);
return;
}
if(index == size()) {
addLast(data);
return;
}
ListNode cur = findIndex(index);
ListNode node = new ListNode(data);
node.next = cur.next;
cur.next = node;}
刪除第一次出現關鍵字為key的結點:
刪除所有值為key的結點: 清空鏈表中所有元素:/**
* 找到 要刪除的關鍵字key的節點
* @param key
* @return
*/public ListNode searchPerv(int key) {
ListNode cur = this.head;
while(cur.next != null) {
if(cur.next.val == key) {
return cur;
}
cur = cur.next;
}
return null;}//刪除第一次出現關鍵字為key的節點public void remove(int key) {
if(this.head == null) {
System.out.println("單鏈表為空");
return;
}
if(this.head.val == key) {
this.head = this.head.next;
return;
}
ListNode cur = searchPerv(key);
if(cur == null) {
System.out.println("沒有你要刪除的節點");
return;
}
ListNode del = cur.next;
cur.next = del.next;}public ListNode removeAllKey(int key) {
if(this.head == null) {
return null;
}
ListNode prev = this.head;
ListNode cur = this.head.next;
while(cur != null) {
if(cur.val == key) {
prev.next = cur.next;
cur = cur.next;
} else {
prev = cur;
cur = cur.next;
}
}
//最后處理頭
if(this.head.val == key) {
this.head = this.head.next;
}
return this.head;}public void clear() {
while (this.head != null) {
ListNode curNext = head.next;
head.next = null;
head.prev = null;
head = curNext;
}
last = null;}

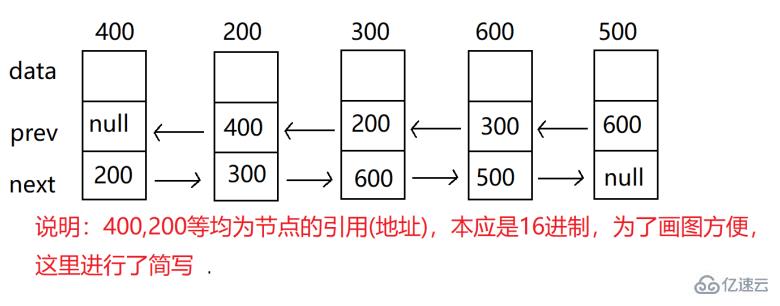
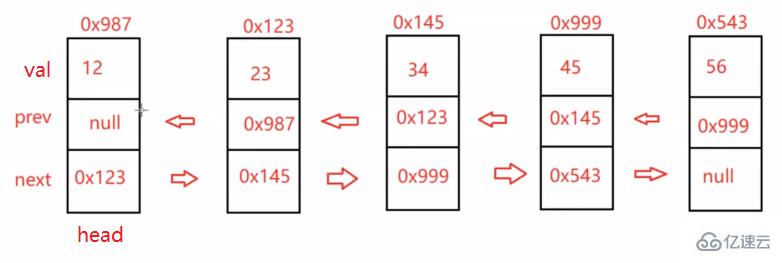
上面的地址0x888為該結點的地址
val:數據域
prev:上一個結點地址
next:下一個結點地址
head:頭結點 一般指向鏈表的第一個結點
上面是我們鏈表的初步結構(未給功能賦相關代碼,大家可以復制他們到自己的idea中進行練習,答案在下文中) 這里我們將他們一個一個拿出來實現 并實現!class ListNode {
public int val;
public ListNode prev;
public ListNode next;
public ListNode (int val) {
this.val = val;
}}public class MyLinkedList {
public ListNode head;//指向雙向鏈表的頭結點
public ListNode last;//只想雙向鏈表的尾結點
//打印鏈表
public void display() {
}
//得到單鏈表的長度
public int size() {
return -1;
}
//查找是否包含關鍵字key是否在單鏈表當中
public boolean contains(int key) {
return true;
}
//頭插法
public void addFirst(int data) {
}
//尾插法
public void addLast(int data) {
}
//刪除第一次出現關鍵字為key的節點
public void remove(int key) {
}
//刪除所有值為key的節點
public void removeAllKey(int key) {
}
//任意位置插入,第一個數據節點為0號下標
public boolean addIndex(int index,int data) {
return true;
}
//清空鏈表
public void clear() {
}}
打印鏈表:
得到單鏈表的長度: 查找是否包含關鍵字key是否在單鏈表當中: 頭插法: 尾插法:public void display() {
ListNode cur = this.head;
while (cur != null) {
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();}public int size() {
ListNode cur = this.head;
int count = 0;
while (cur != null) {
count++;
cur = cur.next;
}
return count;}public boolean contains(int key) {
ListNode cur = this.head;
while (cur != null) {
if (cur.val == key) {
return true;
}
cur = cur.next;
}
return false;}public void addFirst(int data) {
ListNode node = new ListNode(data);
if (this.head == null) {
this.head = node;
this.last = node;
} else {
node.next = this.head;
this.head.prev = node;
this.head = node;
}}public void addLast(int data) {
ListNode node = new ListNode(data);
if (this.head == null) {
this.head = node;
this.last = node;
} else {
ListNode lastPrev = this.last;
this.last.next = node;
this.last = this.last.next;
this.last.prev = lastPrev;
/**
* 兩種方法均可
* this.last.next = node;
* node.prev = this.last;
* this.last = node;
*/
}}
注:第一種方法是先讓last等于尾結點 再讓他的前驅等于上一個地址 而第二種方法是先使插入的尾結點的前驅等于上一個地址 再使其等于尾結點
刪除第一次出現關鍵字為key的結點:
public void remove(int key) {
ListNode cur = this.head;
while (cur != null) {
if (cur.val == key) {
if (cur == head) {
head = head.next;
if (head != null) {
head.prev = null;
} else {
last = null;
}
} else if (cur == last) {
last = last.prev;
last.next = null;
} else {
cur.prev.next = cur.next;
cur.next.prev = cur.prev;
}
return;
}
cur = cur.next;
}}
刪除所有值為key的結點:
public void removeAllKey(int key) {
ListNode cur = this.head;
while (cur != null) {
if (cur.val == key) {
if (cur == head) {
head = head.next;
if (head != null) {
head.prev = null;
} else {
last = null;
}
} else if (cur == last) {
last = last.prev;
last.next = null;
} else {
cur.prev.next = cur.next;
cur.next.prev = cur.prev;
}
//return;
}
cur = cur.next;
}}
注:他和remove的區別就是刪除完后是不是直接return返回,如果要刪除所有的key值則不return,讓cur繼續往后面走。
任意位置插入,第一個數據節點為0號下標:
思路:先判斷 在頭位置就頭插 在尾位置就尾插 在中間就改變四個位置的值。public void addIndex(int index,int data) {
if (index < 0 || index > size()) {
System.out.println("index 位置不合法");
}
if (index == 0) {
addFirst(data);
return;
}
if (index == size()) {
addLast(data);
return;
}
ListNode cur = searchIndex(index);
ListNode node = new ListNode(data);
node.next = cur;
cur.prev.next = node;
node.prev = cur.prev;
cur.prev = node;}public ListNode searchIndex(int index) {
ListNode cur = this.head;
while (index != 0) {
cur = cur.next;
index--;
}
return cur;}
注意:單向鏈表找cur時要-1,但雙向鏈表不用 直接返回cur就好
清空鏈表:
public void clear() {
while (this.head != null) {
ListNode curNext = head.next;
head.next = null;
head.prev = null;
head = curNext;
}
last = null;}
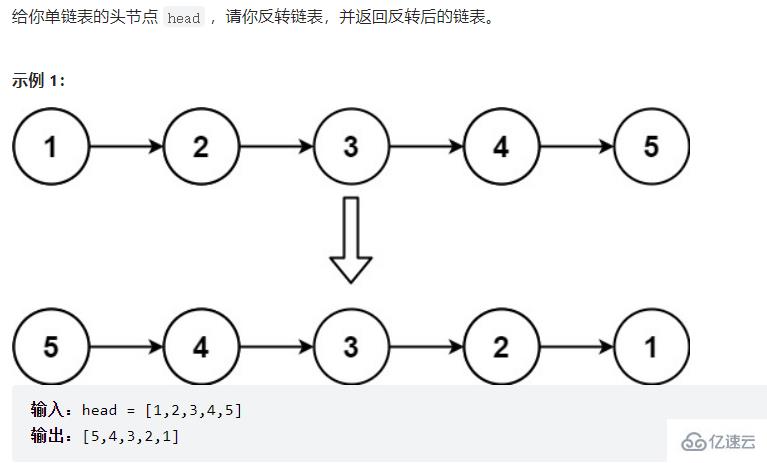

這里的
cur = this.head;
prev = null;
curNext = cur.next;
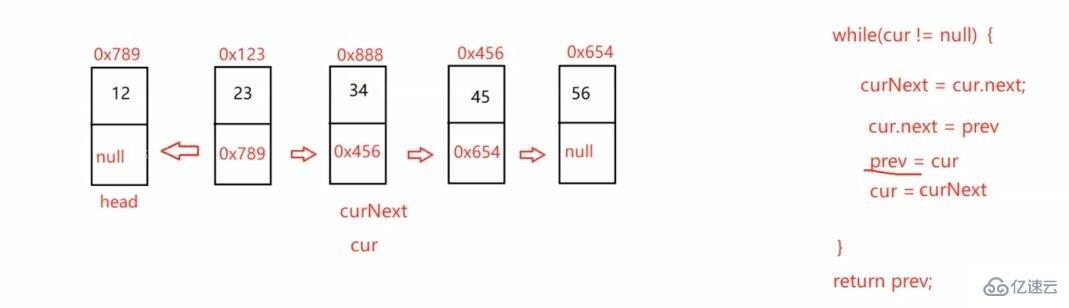
3.3.2找到鏈表的中間結點:public ListNode reverseList() {
if (this.head == null) {
return null;
}
ListNode cur = this.head;
ListNode prev = null;
while (cur != null) {
ListNode curNext = cur.next;
cur.next = prev;
prev = cur;
cur = curNext;
}
return prev;}


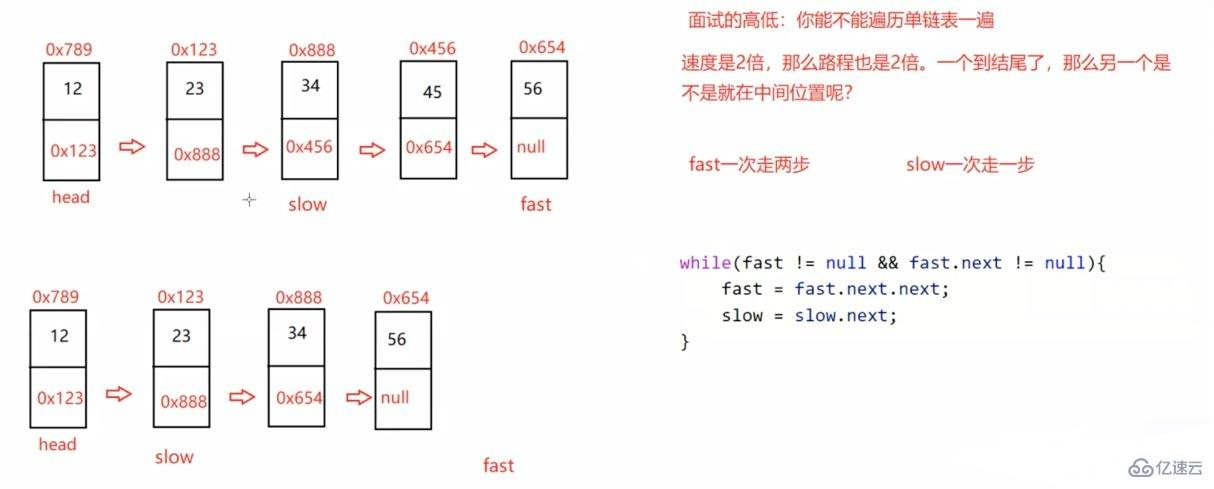
public ListNode middleNode() {
if (head == null) {
return null;
}
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
if (fast == null) {
return slow;
}
slow = slow.next;
}
return slow;}
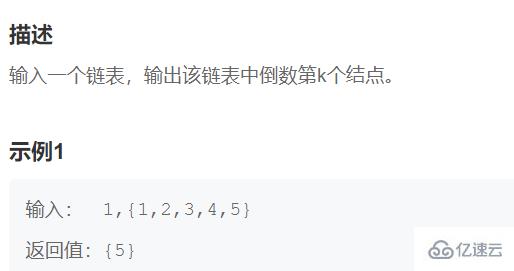
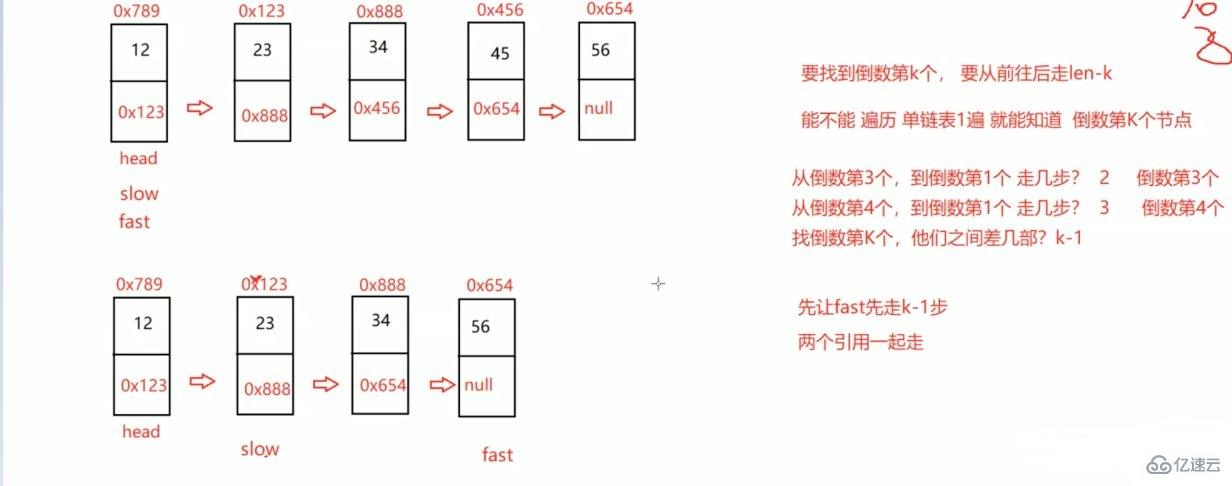
public ListNode findKthToTail(ListNode head,int k) {
if (k <= 0 || head == null) {
return null;
}
ListNode fast = head;
ListNode slow = head;
while (k - 1 != 0) {
fast = fast.next;
if (fast == null) {
return null;
}
k--;
}
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
return slow;}
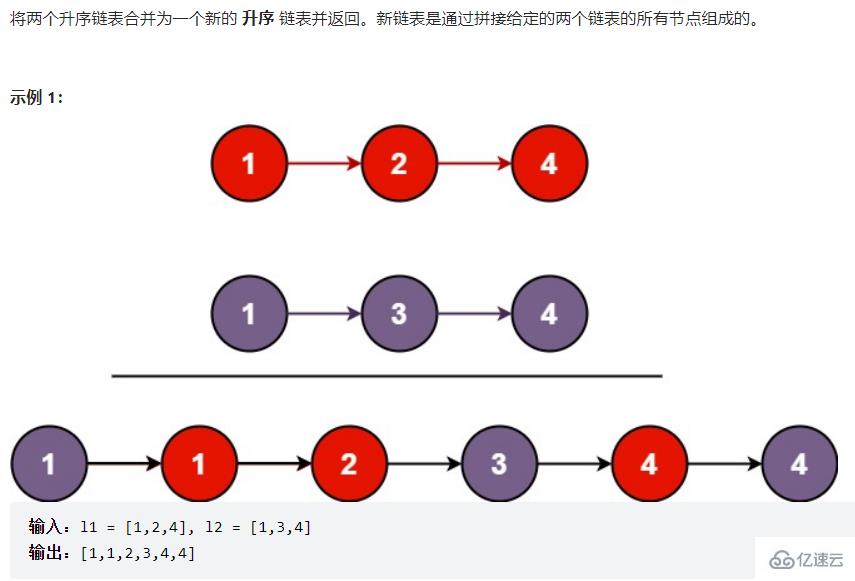

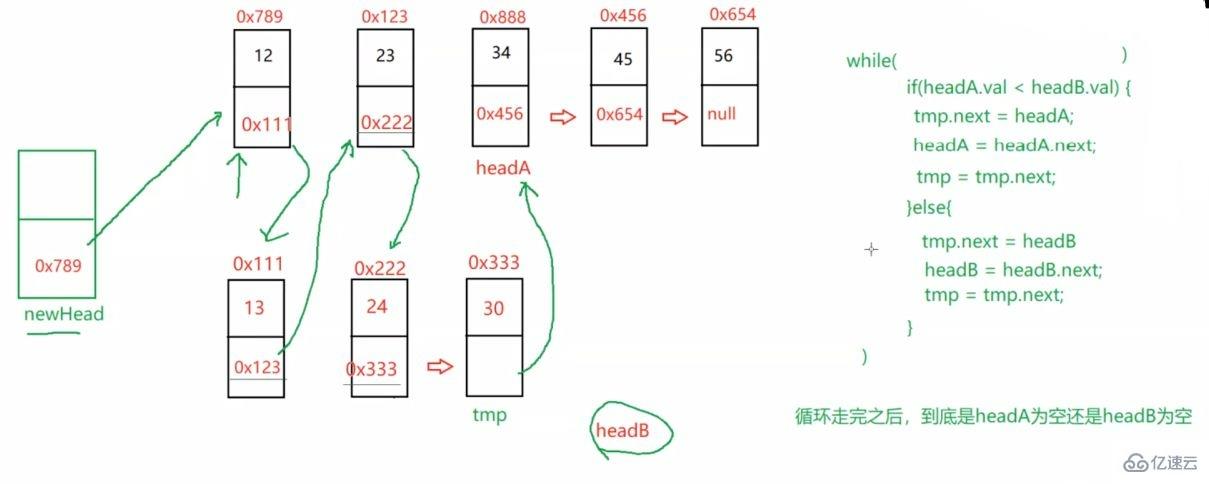
最后返回的是傀儡結點的下一個 即public static ListNode mergeTwoLists(ListNode headA,ListNode headB) {
ListNode newHead = new ListNode(-1);
ListNode tmp = newHead;
while (headA != null && headB != null) {
if(headA.val <headB.val) {
tmp.next = headA;
headA = headA.next;
tmp = tmp.next;
} else {
tmp.next = headB;
headB = headB.next;
tmp = tmp.next;
}
}
if (headA != null) {
tmp.next = headA;
}
if (headB != null) {
tmp.next = headB;
}
return newHead.next;}newHead.next

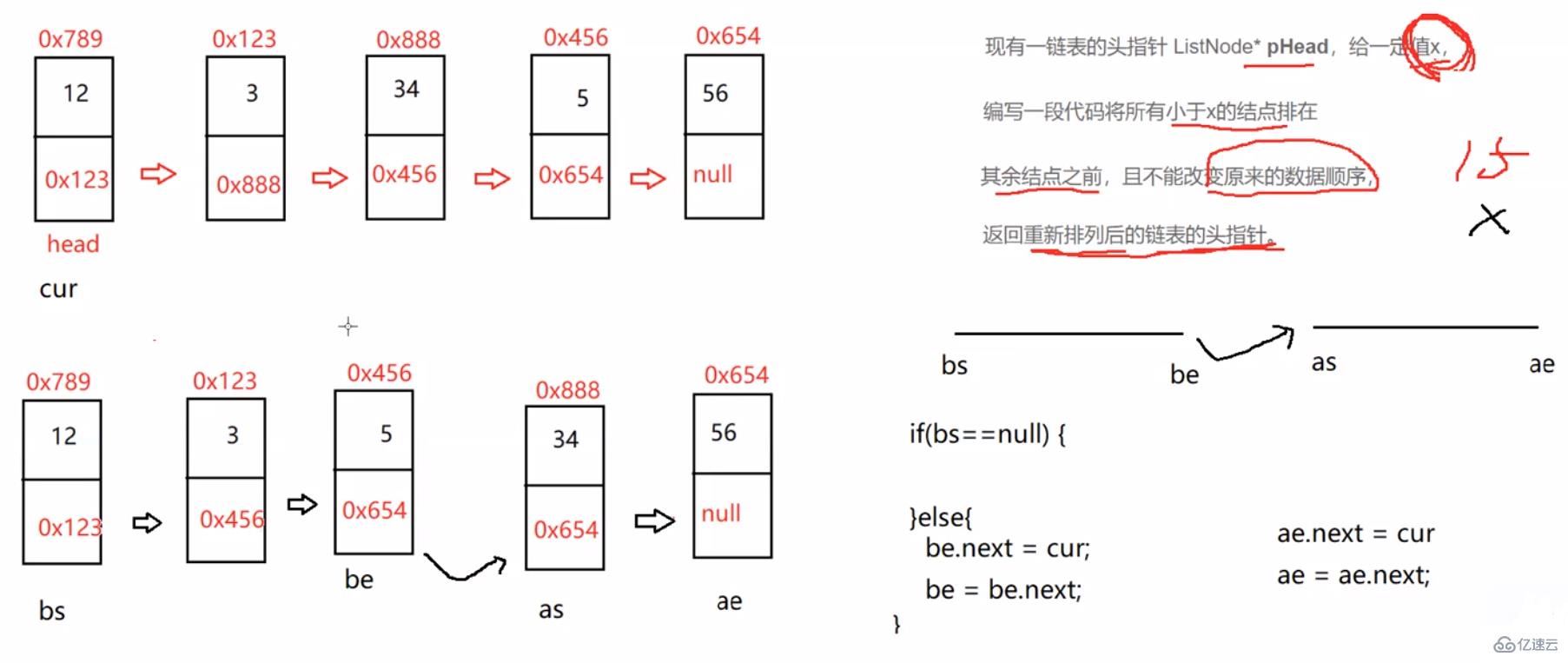
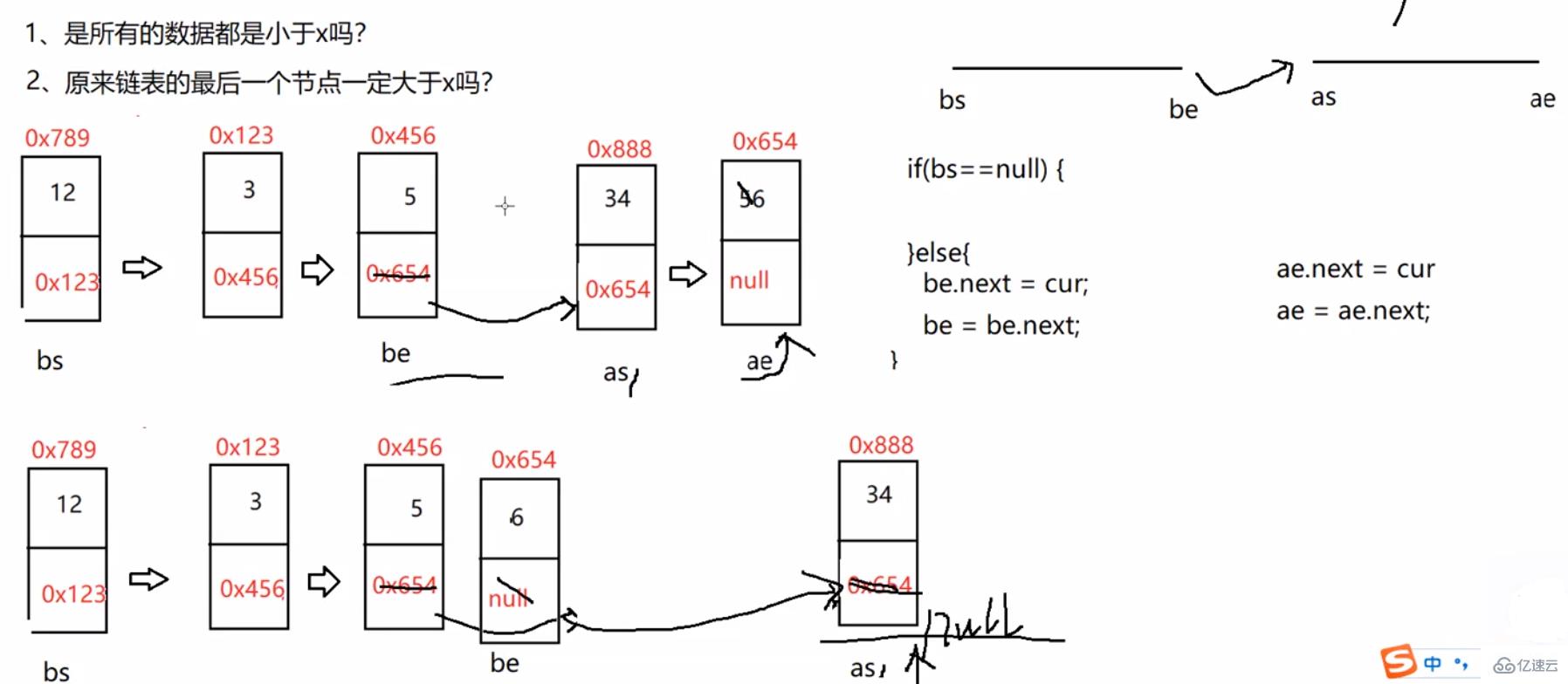
//按照x和鏈表中元素的大小來分割鏈表中的元素public ListNode partition(int x) {
ListNode bs = null;
ListNode be = null;
ListNode as = null;
ListNode ae = null;
ListNode cur = head;
while (cur != null) {
if(cur.val < x){
//1、第一次
if (bs == null) {
bs = cur;
be = cur;
} else {
//2、不是第一次
be.next = cur;
be = be.next;
}
} else {
//1、第一次
if (as == null) {
as = cur;
as = cur;
} else {
//2、不是第一次
ae.next = cur;
ae = ae.next;
}
}
cur = cur.next;
}
//預防第1個段為空
if (bs == null) {
return as;
}
be.next = as;
//預防第2個段當中的數據,最后一個節點不是空的。
if (as != null) {
ae.next = null;
}
return be;}


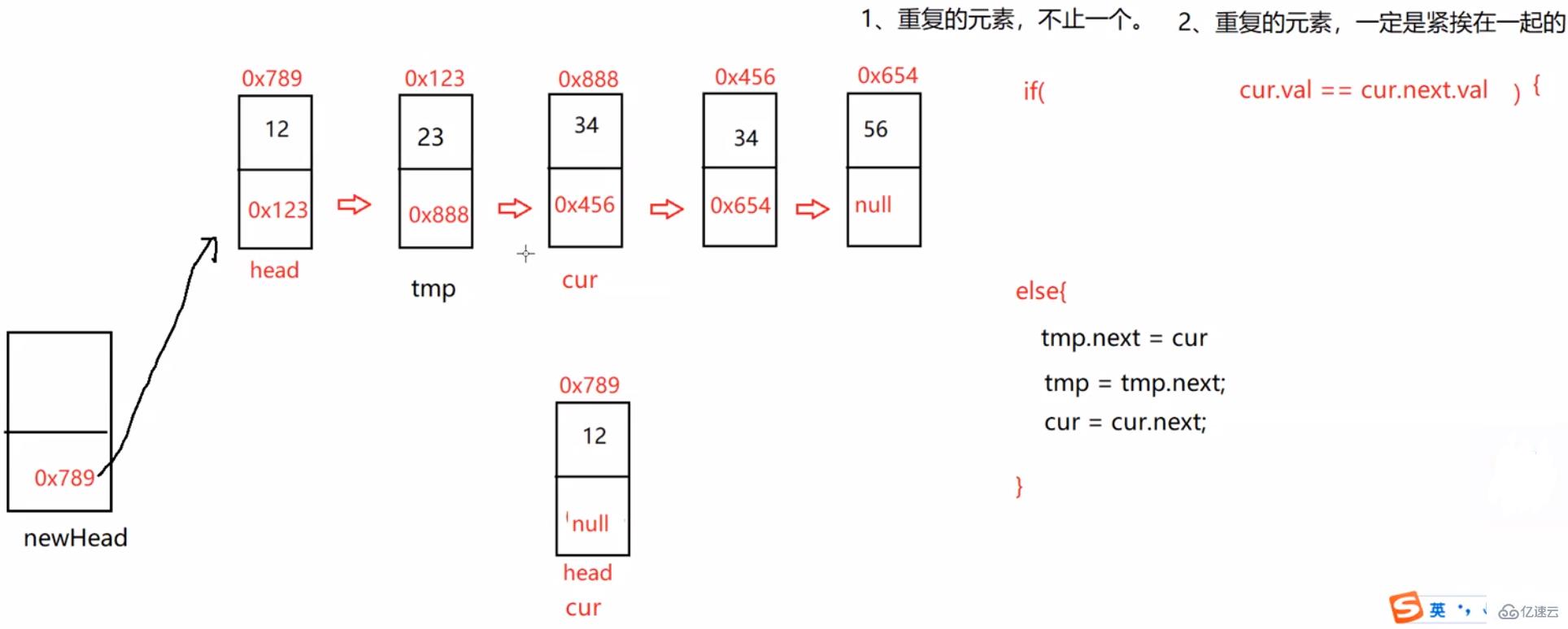
public ListNode deleteDuplication() {
ListNode cur = head;
ListNode newHead = new ListNode(-1);
ListNode tmp = newHead;
while (cur != null) {
if (cur.next != null && cur.val == cur.next.val) {
while (cur.next != null && cur.val == cur.next.val) {
cur = cur.next;
}
//多走一步
cur = cur.next;
} else {
tmp.next = cur;
tmp = tmp.next;
cur = cur.next;
}
}
//防止最后一個結點的值也是重復的
tmp.next = null;
return newHead.next;}

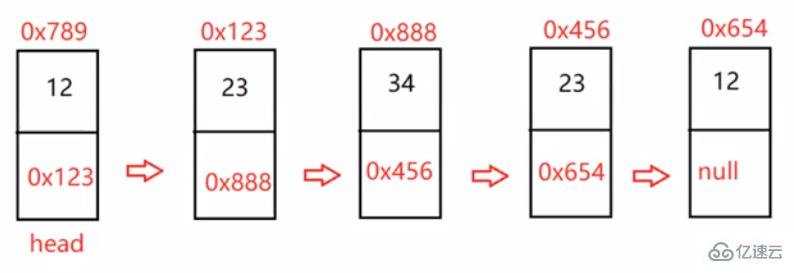
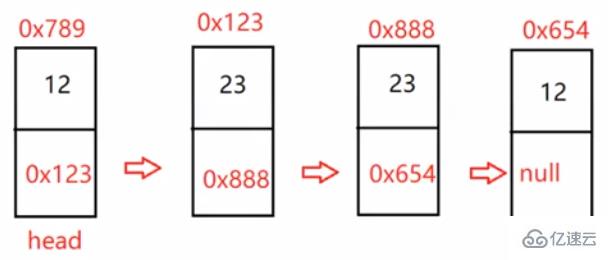
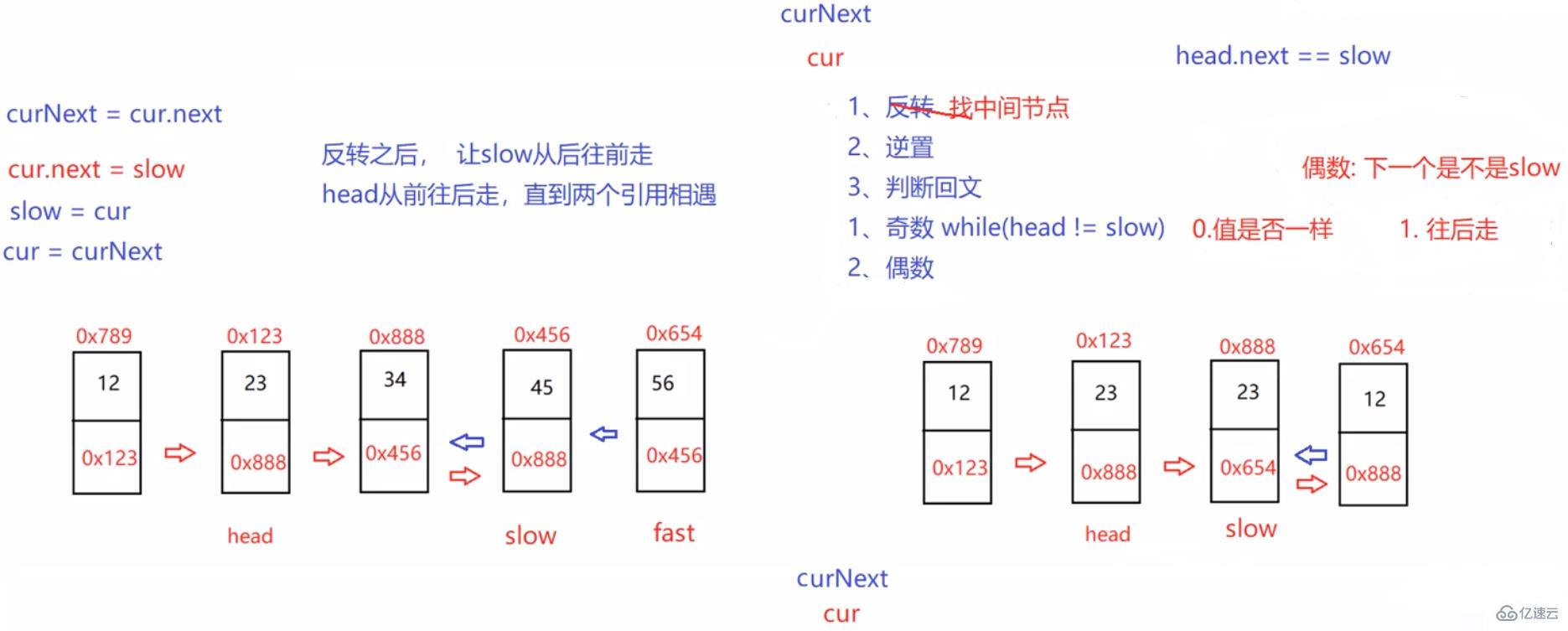
public boolean chkPalindrome(ListNode head) {
if (head == null) {
return true;
}
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
//slow走到了中間位置
ListNode cur = slow.next;
while (cur != null) {
ListNode curNext = cur.next;
cur.next = slow;
slow = cur;
cur = curNext;
}
//反轉完成
while (head != slow) {
if(head.val != slow.val) {
return false;
} else {
if (head.next == slow) {
return true;
}
head = head.next;
slow = slow.next;
}
return true;
}
return true;}
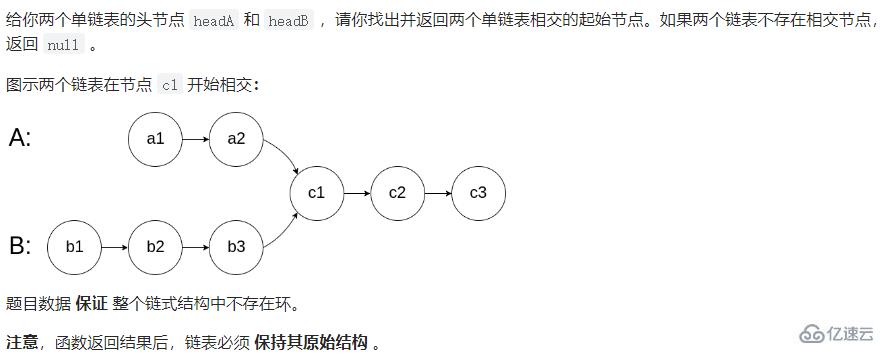
他是一個Y字形
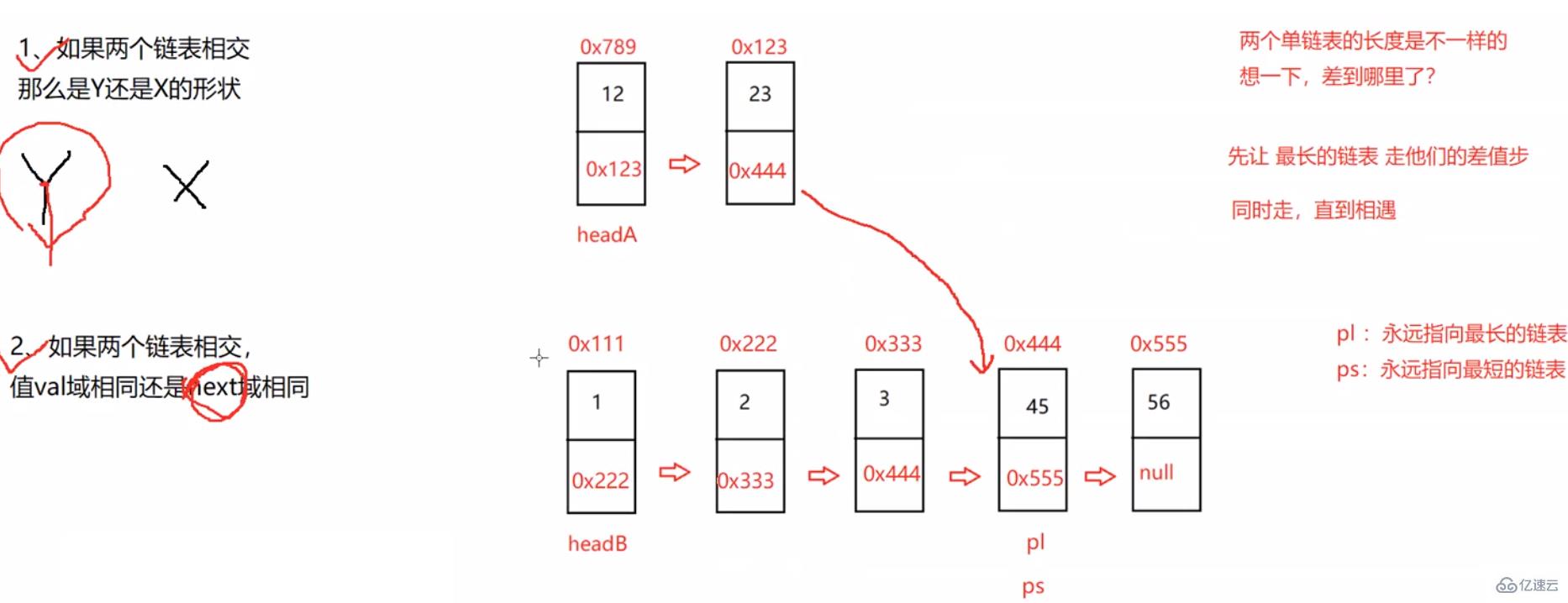

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
ListNode pl = headA;
ListNode ps = headB;
int lenA = 0;
int lenB = 0;
//求lenA的長度
while (pl != null) {
lenA++;
pl = pl.next;
}
pl = headA;
//求lenB的長度
while (ps != null) {
lenB++;
ps = ps.next;
}
ps = headB;
int len = lenA - lenB;//差值步
if (len < 0) {
pl = headB;
ps = headA;
len = lenB - lenA;
}
//1、pl永遠指向了最長的鏈表,ps永遠指向了最短的鏈表 2、求到了插值len步
//pl走差值len步
while (len != 0) {
pl = pl.next;
len--;
}
//同時走直到相遇
while (pl != ps) {
pl = pl.next;
ps = ps.next;
}
return pl;}

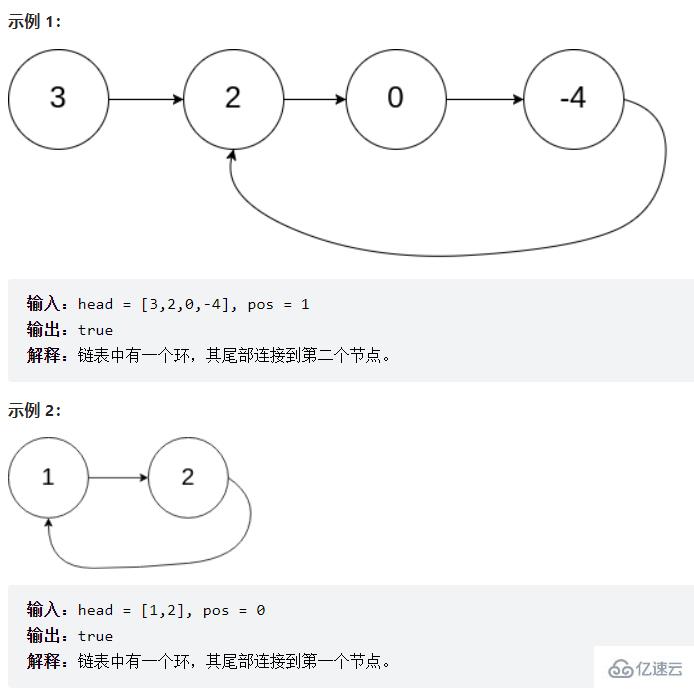

提問:為啥么fast一次走兩步,不走三步?
答:如果鏈表只有兩個元素他們則永遠相遇不了(如上圖的示例2),而且走三步的效率沒有走兩步的效率高。
public boolean hasCycle(ListNode head) {
if (head == null) {
return false;
}
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
return true;
}
}
return false;}

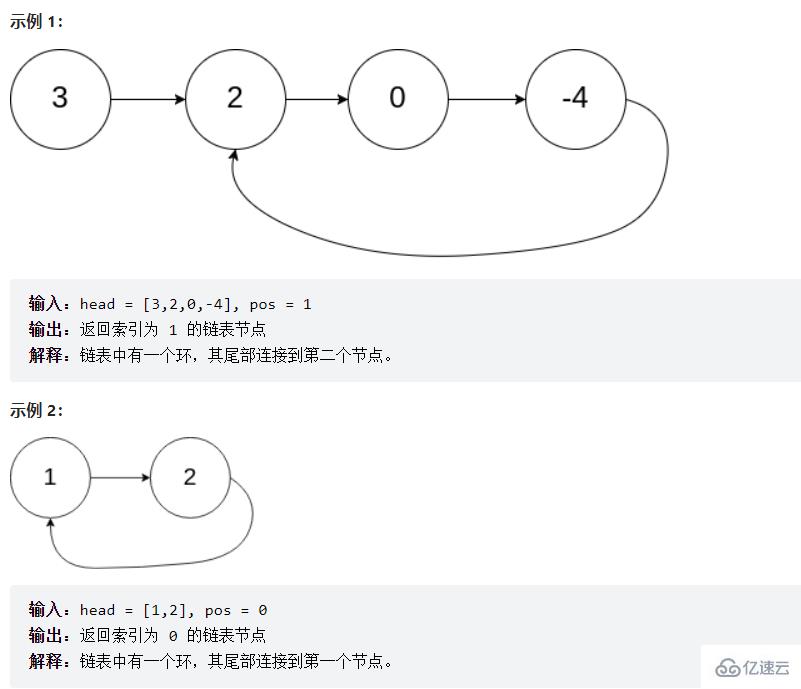

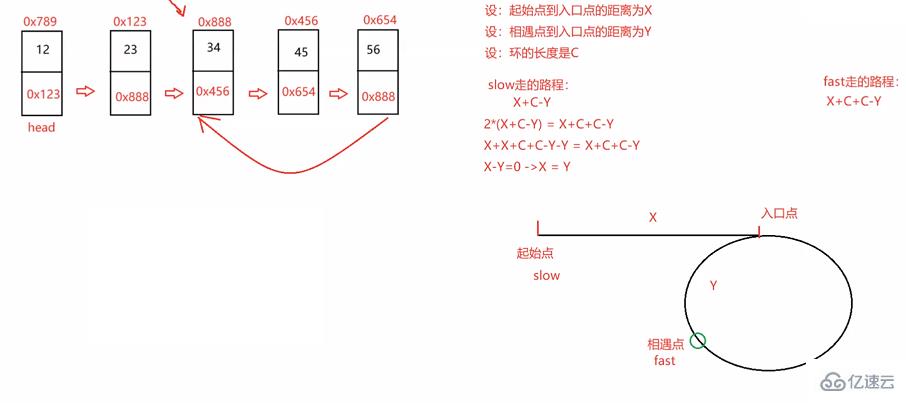
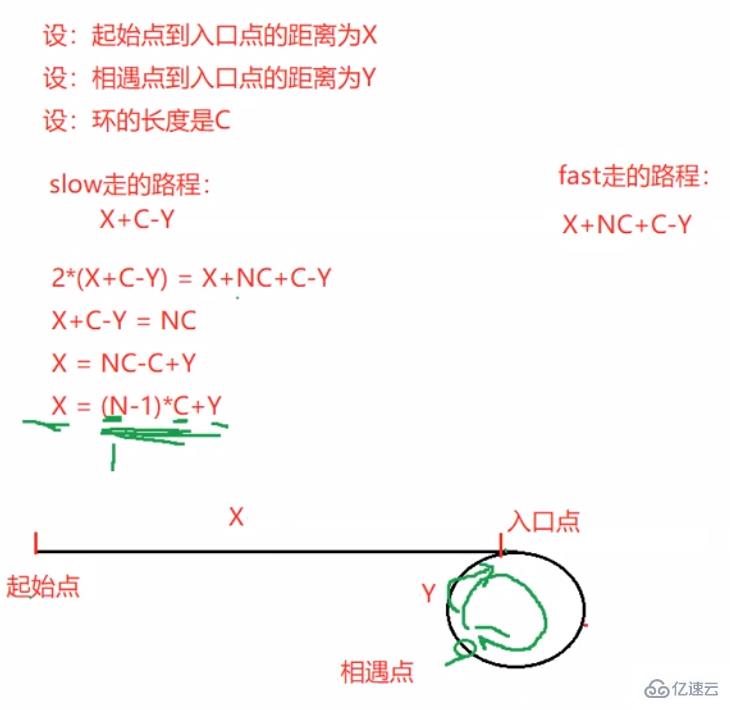
public ListNode detectCycle(ListNode head) {
if (head == null) {
return null;
}
ListNode fast = head;
ListNode slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
break;
}
}
if (fast == null || fast.next == null) {
return null;
}
fast = head;
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return fast;}
順序表:一白遮百丑
白:空間連續、支持隨機訪問
丑:
中間或前面部分的插入刪除時間復雜度O(N)
增容的代價比較大。
鏈表:一(胖黑)毀所有
胖黑:以節點為單位存儲,不支持隨機訪問
所有:
任意位置插入刪除時間復雜度為O(1)
沒有增容問題,插入一個開辟一個空間。
組織:
1、順序表底層是一個數組,他是一個邏輯上和物理上都是連續的
2、鏈表是一個由若干結點組成的一個數據結構,邏輯上是連續的 但是在物理上[內存上]是不一定連續的。
操作:
1、順序表適合,查找相關的操作,因為可以使用下標,直接獲取到某個位置的元素
2、鏈表適合于,頻繁的插入和刪除操作。此時不需要像順序表一樣,移動元素。鏈表的插入 只需要修改指向即可。
3、順序表還有不好的地方,就是你需要看滿不滿,滿了要擴容,擴容了之后,不一定都能放完。所以,他空間上的利用率不高。
鏈表隨用隨取 要一個new一個
而數組則不一樣 數組是一開始就確定好的
集合框架當中的兩個類
集合框架就是將 所有的數據結構,封裝成Java自己的類
以后我們要是用到順序表了 直接使用ArrayList就可以。
以上就是關于“Java順序表和鏈表如何實現”這篇文章的內容,相信大家都有了一定的了解,希望小編分享的內容對大家有幫助,若想了解更多相關的知識內容,請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。