您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“基于Python如何實現二維圖像雙線性插值”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“基于Python如何實現二維圖像雙線性插值”吧!
在對二維數據進行 resize / mapping / 坐標轉換等操作時,經常會將原本的整數坐標變換為小數坐標,對于非整數的坐標值一種直觀有效的插值方式為雙線性插值。
雙線性插值,又稱為雙線性內插。在數學上,雙線性插值是有兩個變量的插值函數的線性插值擴展,其核心思想是在兩個方向分別進行一次線性插值。
雙線性插值作為數值分析中的一種插值算法,廣泛應用在信號處理,數字圖像和視頻處理等方面。
假設我們出現了需要在四個相鄰正方形整數點(A,B,C,D)坐標中間(正方形范圍內)選擇一個點(a,b)取近似值的情形。
此時我們已知的是四個點的數值VA,VB,VC,VD,給定小數坐標E(a,b),0≤a,b≤1,如何插值求解E點的數值呢,解決類似問題的方法統稱為插值,上圖展示公式為雙線性插值的計算方法。
一種最簡便的方法為最近鄰法,直接取與當前點距離最近的點的值作為插值結果:
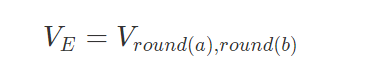
其中 roundroundround 為四舍五入的取整操作,方法簡便速度極快,但往往不夠精細
雙三次插值是用原圖像中16(4*4)個點計算新圖像中1個點,效果比較好,但是計算代價過大。
使用一個點進行插值過于粗暴,16個點又過于繁瑣,那就使用EEE點周圍4個點的數值來近似求解,這是一種平衡了計算代價和插值效果的折中方案,也是各大變換庫的默認插值操作。
通過觀察上述動圖(可以動手挪一挪)可以清晰地看到,雙線性插值本質就是把四個角落的數值按照正方形面積的比例線性加權后的結果。
好吧一句話已經把數學的核心部分講完了
那么既然理解了本質,數學公式就好寫了:
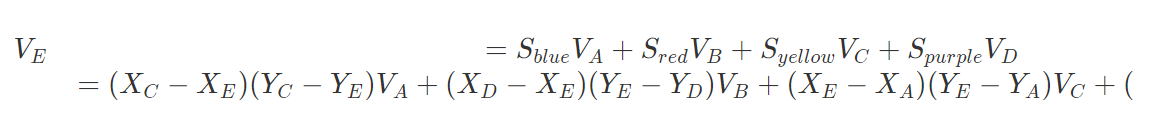
在實現時當然 for 循環大法可以解決一切問題,但總歸是不太優雅,我們嘗試使用 numpy 操作完成雙線性插值
假設原始圖像 image,變換后的小數坐標 X 矩陣 x_grid,Y 矩陣 y_grid,那么可以使用如下的 bilinear_by_meshgrid 函數快速雙線性插值,已經處理好了邊界,可以放心使用。
def bilinear_by_meshgrid(image, x_grid, y_grid):
# Ia, Wd Ic, Wb
# (floor_x, floor_y) (ceil_x, floor_y)
#
# (x, y)
#
# Ib , Wc Id, Wa
# (floor_x, ceil_y) (ceil_x, ceil_y)
#
assert image.shape == x_grid.shape == y_grid.shape
assert image.ndim == 2
H, W = image.shape[:2]
floor_x_grid = np.floor(x_grid).astype('int32')
floor_y_grid = np.floor(y_grid).astype('int32')
ceil_x_grid = floor_x_grid + 1
ceil_y_grid = floor_y_grid + 1
if np.max(ceil_x_grid) > W -1 or np.max(ceil_y_grid) > H -1 or np.min(floor_x_grid) < 0 or np.min(floor_y_grid) < 0:
print("Warning: index value out of original matrix, a crop operation will be applied.")
floor_x_grid = np.clip(floor_x_grid, 0, W-1).astype('int32')
ceil_x_grid = np.clip(ceil_x_grid, 0, W-1).astype('int32')
floor_y_grid = np.clip(floor_y_grid, 0, H-1).astype('int32')
ceil_y_grid = np.clip(ceil_y_grid, 0, H-1).astype('int32')
Ia = image[ floor_y_grid, floor_x_grid ]
Ib = image[ ceil_y_grid, floor_x_grid ]
Ic = image[ floor_y_grid, ceil_x_grid ]
Id = image[ ceil_y_grid, ceil_x_grid ]
wa = (ceil_x_grid - x_grid) * (ceil_y_grid - y_grid)
wb = (ceil_x_grid - x_grid) * (y_grid - floor_y_grid)
wc = (x_grid - floor_x_grid) * (ceil_y_grid - y_grid)
wd = (x_grid - floor_x_grid) * (y_grid - floor_y_grid)
assert np.min(wa) >=0 and np.min(wb) >=0 and np.min(wc) >=0 and np.min(wd) >=0
W = wa + wb + wc + wd
assert np.sum(W[:, -1]) + np.sum(W[-1, :]) == 0
wa[:-1, -1] = ceil_y_grid[:-1, -1] - y_grid[:-1, -1]
wb[:-1, -1] = y_grid[:-1, -1] - floor_y_grid[:-1, -1]
wb[-1, :-1] = ceil_x_grid[-1, :-1] - x_grid[-1, :-1]
wd[-1, :-1] = x_grid[-1, :-1] - floor_x_grid[-1, :-1]
wd[-1, -1] = 1
W = wa + wb + wc + wd
assert np.max(W) == np.min(W) == 1
res_image = wa*Ia + wb*Ib + wc*Ic + wd*Id
return res_image該函數集成在我自己的python庫 mtutils 中,可以通過:
pip install mtutils
直接安裝,之后可以直接引用:
from mtutils import bilinear_by_meshgrid
到此,相信大家對“基于Python如何實現二維圖像雙線性插值”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。