您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了C#如何實現二叉查找樹的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇C#如何實現二叉查找樹文章都會有所收獲,下面我們一起來看看吧。
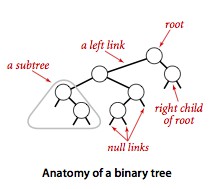
對于符號表,要支持高效的插入操作,就需要一種鏈式結構。但單鏈表無法使用二分查找,因為二分查找的高效來自于能夠快速通過索引取得任何子數組的中間元素,鏈表只能遍歷(詳細描述)。為了將二分查找的效率和鏈表的靈活性結合,需要更復雜的數據結構:二叉查找樹。具體來說,就是使用每個結點含有兩個鏈接的二叉查找樹來高效地實現符號表。
一棵二叉查找樹(BST)是一棵二叉樹,其中每個結點都含有一個IComparable 類型的鍵以及相關聯的值,且每個結點的鍵都大于其左子樹的任意結點的鍵而小于右子樹的任意結點的鍵。
public class BinarySearchTreesST<Key, Value> : BaseSymbolTables<Key, Value>
where Key : IComparable
{
private Node root;//二叉樹根節點
/// <summary>
/// 嵌套定義一個私有類表示二叉查找樹上的一個結點。
/// 每個結點都含有一個鍵,一個值,一條左連接,一條右連接和一個結點計數器。
/// 變量 N 給出了以該結點為根的子樹的結點總數。
/// x.N = Size(x.left) + Size(x.right) + 1;
/// </summary>
private class Node
{
public Key key;
public Value value;
public Node left, right;
public int N;
public Node(Key key,Value value,int N)
{
this.key = key;
this.value = value;
this.N = N;
}
}
public override int Size()
{
return Size(root);
}
private int Size(Node x)
{
if (x == null)
return 0;
else
return x.N;
}
}一棵二叉查找樹代表了一組鍵(及其相應的值)的集合,而一個可以用多棵不同的二叉查找樹表(起始根結點不同,樹就不同),下面是一種情況。但不管什么情況的樹,我們將一棵二叉查找樹的所有鍵投影到一條直線上,一定可以得到一條有序的鍵列。
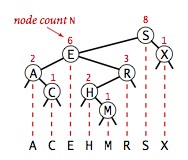
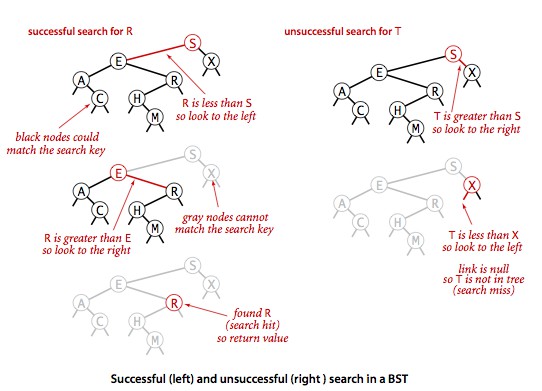
在符號表中查找一個鍵可能有兩種結果:命中和未命中。下面的實現算法是在二叉查找樹中查找一個鍵的遞歸算法:如果樹是空的,則查找未命中,如果被查找的鍵和根結點的鍵相等,查找命中,否則就遞歸地在適當地子樹中繼續查找。如果被查找的鍵較小就選擇左子樹,較大則選擇右子樹。當找到一個含有被查找鍵的結點(命中)或者當前子樹變為空(未命中)時這個過程才結束。
public override Value Get(Key key)
{
return Get(root,key);
}
/// <summary>
///
/// </summary>
/// <param name="x">第一個參數是結點(子樹的根結點)</param>
/// <param name="key">第二個參數是被查找的鍵</param>
/// <returns></returns>
private Value Get(Node x, Key key)
{
if (x == null)
return default(Value);
int cmp = key.CompareTo(x.key);
if (cmp < 0)
return Get(x.left, key);
else if (cmp > 0)
return Get(x.right, key);
else
return x.value;
}
插入方法和查找的實現差不多,當查找一個不存在于樹中的結點并結束于一條空連接時,需要將連接指向一個含有被查找的鍵的新節點。下面插入方法的邏輯:如果樹是空的,就返回一個含有該鍵值對的新結點賦值給這個空連接;如果被查找的鍵小于根結點的鍵,繼續在左子樹中插入該鍵,否則就在右子樹中插入。并且需要更新計數器。
public override void Put(Key key, Value value)
{
root = Put(root,key,value);
}
private Node Put(Node x, Key key, Value value)
{
if (x == null)
return new Node(key,value,1);
int cmp = key.CompareTo(x.key);
if (cmp < 0)
x.left = Put(x.left, key, value); //注意 x.left = 的意思
else if (cmp > 0)
x.right = Put(x.right, key, value);//注意 x.right =
else
x.value = value;
x.N = Size(x.left) + Size(x.right) + 1;
return x;
}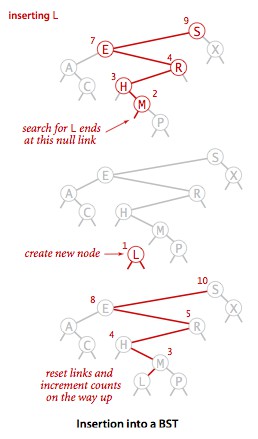
在查找和插入的遞歸實現中,可以將遞歸調用前的代碼想象成沿著樹向下走,將遞歸調用后的代碼想象成沿著樹向上爬。對于 Get 方法,這對應著一系列的返回指令。對于 Put 方法,意味著重置搜索路徑上每個父結點指向子結點的連接,并增加路徑上每個結點中計數器的值。在一棵簡單的二叉查找樹中,唯一的新連接就是在最底層指向新結點的連接,重置更上層的連接可以通過比較語句來避免。
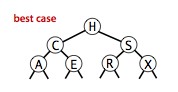
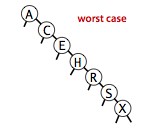
二叉查找樹上算法的運行時間取決于樹的形狀,而樹的形狀又取決于鍵的插入順序。在最好情況下,一棵含有 N 個結點的樹是完全平衡的,每條空連接和根結點的距離都是 ~lgN 。在最壞情況下,搜索路徑上有 N 個結點。
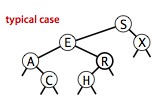
對于隨機模型的分析而言,二叉查找樹和快速排序很相似。根結點就是快速排序中的第一個切分元素,對于其他子樹也同樣使用。
在由 N 個隨機鍵構造的二叉查找樹,查找命中的平均所需的比較次數為 ~2lnN (約1.39lgN),插入和查找未命中平均所需的比較次數也為~2lnN (約1.39lgN)。插入和查找未命中比查找命中需要一次額外比較。
由此可知,在二叉查找樹中查找比二分查找的成本高出約 39% ,但是插入操作所需的成本達到了對數界別。
如果根結點的左連接為空,那么一棵二叉查找樹中最小的鍵就是根結點;如果左連接非空,那么樹中的最小鍵就是左子樹中的最小鍵。
public override Key Min()
{
return Min(root).key;
}
private Node Min(Node x)
{
if (x.left == null)
return x;
return Min(x.left);
}如果給定的鍵 key 小于二叉查找樹的根結點的鍵,那么小于等于 key 的最大鍵 Floor( key ) 一定在根結點的左子樹中;如果給定的鍵大于二叉查找樹的根結點,那么只有當根節點的右子樹中存在小于等于給定鍵的結點時,小于等于給定鍵的最大鍵才會出現在右子樹中,否則根結點就是小于等于 key 的最大鍵。
/// <summary>
/// 向下取整
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
public override Key Floor(Key key)
{
Node x = Floor(root,key);
if (x == null)
return default(Key);
return x.key;
}
private Node Floor(Node x, Key key)
{
if (x == null)
return default(Node);
int cmp = key.CompareTo(x.key);
if (cmp == 0)
return x;
if (cmp < 0)
return Floor(x.left,key);
Node t = Floor(x.right,key);
if (t != null)
return t;
else
return x;
}我們在二叉查找樹的每個結點中維護的子樹結點計數器變量 N 就是用來支持此操作的。
如果要找到排名為 k 的鍵(即樹中正好有 k 個小于它的鍵)。如果左子樹中的結點樹 t 大于 k,就繼續(遞歸地)在左子樹中查找排名為 k 的鍵;如果 t == k,就返回根結點的鍵;如果 t 小于 k,就遞歸地在右子樹中查找排名為 (k-t-1)的鍵。
public override Key Select(int k)
{
return Select(root, k).key;
}
private Node Select(Node x, int k)
{
if (x == null)
return default(Node);
int t = Size(x.left);
if (t > k)
return Select(x.left, k);
else if (t < k)
return Select(x.right, k - t - 1);
else
return x;
}排名是選擇操作的逆方法,它會返回給定鍵的排名。它的實現和 Select 類似:如果給定的鍵等于根根結點的鍵,就返回左子樹中的節點數 t ;如果給定的鍵小于根結點,就返回該鍵在左子樹中的排名(遞歸計算);如果給定的鍵大于根結點,就返回 t+1 (根結點)再加上它在右子樹中的排名(遞歸計算)。
public override int Rank(Key key)
{
return Rank(key,root);
}
private int Rank(Key key, Node x)
{
if (x == null)
return 0;
int cmp = key.CompareTo(x.key);
if (cmp < 0)
return Rank(key, x.left);
else if (cmp > 0)
return 1 + Size(x.left) + Rank(key, x.right);
else
return Size(x.left);
}二叉查找樹中最難實現的就是刪除操作,我們先實現刪除最小鍵的操作。我們要不斷深入根節點的左子樹直到遇到一個空連接,然后將指向該結點的連接指向該結點的右子樹(只需在 x.left == null 時返回右鏈接,賦值給上層的左連接)。
/// <summary>
/// 注意可考慮刪除根結點
/// </summary>
public override void DeleteMin()
{
root = DeleteMin(root);
}
private Node DeleteMin(Node x)
{
if (x.left == null)
return x.right;
x.left = DeleteMin(x.left);
x.N = Size(x.left) + Size(x.right) + 1;
return x;
}我們 可以使用上面類似的方法刪除任意只有一個子結點或者沒有子結點的結點,但是無法實現刪除有兩個子結點的結點的方法。我們在刪除 x 結點后用它的右子樹最小結點結點填補它的位置,這樣就可以保證樹的有序性,分四步完成:
1.將指向即將被刪除的結點的連接保存為 t ;
2.將 x 指向它的后繼結點 Min(t.right);
3.將 x 的右鏈接指向 DeleteMin(t.right),也就是刪除右子樹最小連接,然后返回 t 的右鏈接;
4.將 x 的左連接設為 t.left;
public override void Delete(Key key)
{
root = Delete(root,key);
}
private Node Delete(Node x, Key key)
{
if (x == null)
return null;
int cmp = key.CompareTo(x.key);
if (cmp < 0)
x.left = Delete(x.left, key);
else if (cmp > 0)
x.right = Delete(x.right, key);
else
{
if (x.right == null)
return x.left;
if (x.left == null)
return x.right;
Node t = x;
x = Min(t.right);
x.right = DeleteMin(t.right);
x.left = t.left;
}
x.N = Size(x.left) + Size(x.right) + 1;
return x;
}該算法有個問題,在選擇后繼結點應該是隨機的,應該考慮樹的對成性。
要實現能夠返回給定范圍內鍵的方法 Keys(),需要一個遍歷二叉查找樹的基本方法,叫做中序遍歷。先找出根結點的左子樹中的符合的所有鍵,然后找出根結點的鍵,最后找出根結點右子樹的符合的所有鍵。
public override IEnumerable<Key> Keys(Key lo, Key hi)
{
Queue<Key> quene = new Queue<Key>();
Keys(root, quene,lo,hi);
return quene;
}
private void Keys(Node x, Queue<Key> quene, Key lo, Key hi)
{
if (x == null)
return;
int cmplo = lo.CompareTo(x.key);
int cmphi = hi.CompareTo(x.key);
if (cmplo < 0)
Keys(x.left,quene,lo,hi);
if (cmplo <= 0 && cmphi >= 0)
quene.Enqueue(x.key);
if (cmphi > 0)
Keys(x.right,quene,lo,hi);
}全部代碼
public class BinarySearchTreesST<Key, Value> : BaseSymbolTables<Key, Value>
where Key : IComparable
{
private Node root;//二叉樹根節點
/// <summary>
/// 嵌套定義一個私有類表示二叉查找樹上的一個結點。
/// 每個結點都含有一個鍵,一個值,一條左連接,一條右連接和一個結點計數器。
/// 變量 N 給出了以該結點為根的子樹的結點總數。
/// x.N = Size(x.left) + Size(x.right) + 1;
/// </summary>
private class Node
{
public Key key;
public Value value;
public Node left, right;
public int N;
public Node(Key key,Value value,int N)
{
this.key = key;
this.value = value;
this.N = N;
}
}
public override int Size()
{
return Size(root);
}
private int Size(Node x)
{
if (x == null)
return 0;
else
return x.N;
}
public override Value Get(Key key)
{
return Get(root,key);
}
/// <summary>
///
/// </summary>
/// <param name="x">第一個參數是結點(子樹的根結點)</param>
/// <param name="key">第二個參數是被查找的鍵</param>
/// <returns></returns>
private Value Get(Node x, Key key)
{
if (x == null)
return default(Value);
int cmp = key.CompareTo(x.key);
if (cmp < 0)
return Get(x.left, key);
else if (cmp > 0)
return Get(x.right, key);
else
return x.value;
}
public override void Put(Key key, Value value)
{
root = Put(root,key,value);
}
private Node Put(Node x, Key key, Value value)
{
if (x == null)
return new Node(key,value,1);
int cmp = key.CompareTo(x.key);
if (cmp < 0)
x.left = Put(x.left, key, value); //注意 x.left = 的意思
else if (cmp > 0)
x.right = Put(x.right, key, value);//注意 x.right =
else
x.value = value;
x.N = Size(x.left) + Size(x.right) + 1;
return x;
}
public override Key Min()
{
return Min(root).key;
}
private Node Min(Node x)
{
if (x.left == null)
return x;
return Min(x.left);
}
/// <summary>
/// 向下取整
/// </summary>
/// <param name="key"></param>
/// <returns></returns>
public override Key Floor(Key key)
{
Node x = Floor(root,key);
if (x == null)
return default(Key);
return x.key;
}
private Node Floor(Node x, Key key)
{
if (x == null)
return default(Node);
int cmp = key.CompareTo(x.key);
if (cmp == 0)
return x;
if (cmp < 0)
return Floor(x.left,key);
Node t = Floor(x.right,key);
if (t != null)
return t;
else
return x;
}
public override Key Select(int k)
{
return Select(root, k).key;
}
private Node Select(Node x, int k)
{
if (x == null)
return default(Node);
int t = Size(x.left);
if (t > k)
return Select(x.left, k);
else if (t < k)
return Select(x.right, k - t - 1);
else
return x;
}
public override int Rank(Key key)
{
return Rank(key,root);
}
private int Rank(Key key, Node x)
{
if (x == null)
return 0;
int cmp = key.CompareTo(x.key);
if (cmp < 0)
return Rank(key, x.left);
else if (cmp > 0)
return 1 + Size(x.left) + Rank(key, x.right);
else
return Size(x.left);
}
/// <summary>
/// 注意可考慮刪除根結點
/// </summary>
public override void DeleteMin()
{
root = DeleteMin(root);
}
private Node DeleteMin(Node x)
{
if (x.left == null)
return x.right;
x.left = DeleteMin(x.left);
x.N = Size(x.left) + Size(x.right) + 1;
return x;
}
public override void Delete(Key key)
{
root = Delete(root,key);
}
private Node Delete(Node x, Key key)
{
if (x == null)
return null;
int cmp = key.CompareTo(x.key);
if (cmp < 0)
x.left = Delete(x.left, key);
else if (cmp > 0)
x.right = Delete(x.right, key);
else
{
if (x.right == null)
return x.left;
if (x.left == null)
return x.right;
Node t = x;
x = Min(t.right);
x.right = DeleteMin(t.right);
x.left = t.left;
}
x.N = Size(x.left) + Size(x.right) + 1;
return x;
}
public override IEnumerable<Key> Keys(Key lo, Key hi)
{
Queue<Key> quene = new Queue<Key>();
Keys(root, quene,lo,hi);
return quene;
}
private void Keys(Node x, Queue<Key> quene, Key lo, Key hi)
{
if (x == null)
return;
int cmplo = lo.CompareTo(x.key);
int cmphi = hi.CompareTo(x.key);
if (cmplo < 0)
Keys(x.left,quene,lo,hi);
if (cmplo <= 0 && cmphi >= 0)
quene.Enqueue(x.key);
if (cmphi > 0)
Keys(x.right,quene,lo,hi);
}
}給定一棵樹,樹的高度決定了所有操作在最壞情況下的性能(范圍查找除外,因為它的額外成本和返回的鍵的數量成正比),成正比。
隨機構造的二叉查找樹的平均高度為樹中結點數量的對數級別,約為 2.99 lgN 。但如果構造樹的鍵不是隨機的(例如,順序或者倒序),性能會大大降低,后面會講到平衡二叉查找樹。
| 算法 | 最壞情況下運行時間的增長量級 | 平均情況下的運行時間的增長量級 | 是否支持有序性相關操作 | ||
| 查找 | 插入 | 查找命中 | 插入 | ||
| 順序查找(無序鏈表) | N | N | N/2 | N | 否 |
| 二分查找(有序數組) | lgN | N | lgN | N/2 | 是 |
| 二叉樹查找 | N | N | 1.39lgN | 1.39lgN | 是 |
關于“C#如何實現二叉查找樹”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“C#如何實現二叉查找樹”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。