C#如何實現簡單的二叉查找樹

本篇內容介紹了“C#如何實現簡單的二叉查找樹”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

二叉查找樹（Binary Search Tree），或者是一棵空樹，或者是具有下列性質的二叉樹：

• 若它的左子樹不空，則左子樹上所有結點的值均小于它的根結點的值；

• 若它的右子樹不空，則右子樹上所有結點的值均大于它的根結點的值；

• 它的左、右子樹也分別為二叉排序樹。

二叉排序樹的查找過程和次優二叉樹類似，通常采取二叉鏈表作為二叉排序樹的存儲結構。中序遍歷二叉排序樹可得到一個關鍵字的有序序列，一個無序序列可以通過構造一棵二叉排序樹變成一個有序序列，構造樹的過程即為對無序序列進行排序的過程。每次插入的新的結點都是二叉排序樹上新的葉子結點，在進行插入操作時，不必移動其它結點，只需改動某個結點的指針，由空變為非空即可。搜索,插入,刪除的復雜度等于樹高，O(log(n))。

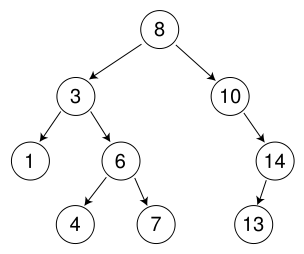
圖 1. 三層二叉查找樹

二叉排序樹典型的用途是實現關聯數組，一種常用的定義方式為：

class BiTree<TKey,TValue> where TKey:IComparable
{
    public TKey Key { get; set; }
    public TValue Value { get; set; }

    BiTree<TKey, TValue> Left { get; set; }
    BiTree<TKey, TValue> Right { get; set; }

    public BiTree(TKey key,TValue value)
    {
        this.Key = key;
        this.Value = value;
    }
}

二叉排序樹的查找算法

在二叉排序樹b中查找x的過程為：

• 若b是空樹，則搜索失敗，否則：

• 若x等于b的根結點的數據域之值，則查找成功；否則：

• 若x小于b的根結點的數據域之值，則搜索左子樹；否則：

• 查找右子樹。

public TValue Search(TKey key)
{
    int ret = key.CompareTo(this.Key);

    if (ret == 0)
    {
        return Value;
    }
    else
    {
        var subTree = ret < 0 ? Left : Right;
        if (subTree == null)
        {
            throw new KeyNotFoundException();
        }
        else
        {
            return subTree.Search(key);
        }
    }
}

在二叉排序樹插入結點的算法

一種簡單的向一個二叉排序樹b中插入一個結點s的算法為：

• 若b是空樹，則將s所指結點作為根結點插入，否則：

• 若s->data等于b的根結點的數據域之值，則返回，否則：

• 若s->data小于b的根結點的數據域之值，則把s所指結點插入到左子樹中，否則：

• 把s所指結點插入到右子樹中。

public void Insert(TKey key, TValue value)
{
    int ret = key.CompareTo(this.Key);

    if (ret == 0)
    {
        this.Value = value;
    }
    else
    {
        var subTree = ret < 0 ? Left : Right;
        if (subTree == null)
        {
            subTree = new BiTree<TKey, TValue>(key, value);
            if (ret < 0)
                Left = subTree;
            else
                Right = subTree;
        }
        else
        {
            subTree.Insert(key, value);
        }
    }
}

在二叉排序樹刪除結點的算法

在二叉排序樹刪去一個結點，分三種情況討論：

• 若*p結點為葉子結點，即PL(左子樹)和PR(右子樹)均為空樹。由于刪去葉子結點不破壞整棵樹的結構，則只需修改其雙親結點的指針即可。

• 若*p結點只有左子樹PL或右子樹PR，此時只要令PL或PR直接成為其雙親結點*f的左子樹即可，作此修改也不破壞二叉排序樹的特性。

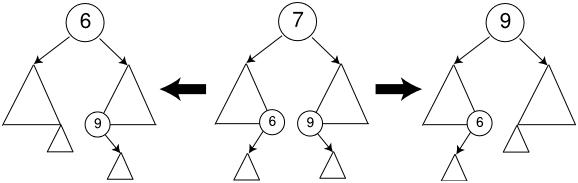
• 若*p結點的左子樹和右子樹均不空。在刪去*p之后，為保持其它元素之間的相對位置不變，可按中序遍歷保持有序進行調整，可以有兩種做法：其一是令*p的左子樹為*f的左子樹，*s為*f左子樹的最右下的結點，而*p的右子樹為*s的右子樹；其二是令*p的直接前驅（或直接后繼）替代*p，然后再從二叉排序樹中刪去它的直接前驅（或直接后繼）。

二叉排序樹性的遍歷

二叉排序樹一般采用先根訪問，這樣能將所有元素按大小排序訪問。

public void Visit(Action<TKey, TValue> visitor)
{
    if (Left != null)
    {
        Left.Visit(visitor);
    }

    visitor(Key, Value);

    if (Right != null)
    {
        Right.Visit(visitor);
    }
}

二叉排序樹性能分析

每個結點的Ci為該結點的層次數。最壞情況下，當先后插入的關鍵字有序時，構成的二叉排序樹蛻變為單支樹，樹的深度為n，其平均查找長度為

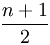
（和順序查找相同），最好的情況是二叉排序樹的形態和折半查找的判定樹相同，其平均查找長度和log2(n)成正比（O(log2(n))）。

“C#如何實現簡單的二叉查找樹”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！