您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了Java這么實現無向圖的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇Java這么實現無向圖文章都會有所收獲,下面我們一起來看看吧。
一個圖是由點集V={vi} 和 VV 中元素的無序對的一個集合E={ek} 所構成的二元組,記為G=(V,E),V中的元素vi叫做頂點,E中的元素 ek叫做邊。
對于V中的兩個點 u,v,如果邊(u,v) 屬于E,則稱 u,v兩點相鄰,u,v稱為邊(u,v)的端點。
我們可以用m(G)=|E| 表示圖G中的邊數,用n(G)=|V|表示圖G中的頂點個數。
對于E中的任意一條邊(vi,vj),如果邊(vi,vj) 端點無序,則它是無向邊,此時圖G稱為無向圖。無向圖是最簡單的圖模型,下圖顯示了同一幅無向圖,頂點使用圓圈表示,邊則是頂點之間的連線,沒有箭頭(圖片來自于《算法第四版》):

對于一幅無向圖,我們關心圖的頂點數、邊數、每個頂點的相鄰頂點和邊的添加操作,所以接口如下所示:
package com.zhiyiyo.graph;
/**
* 無向圖
*/
public interface Graph {
/**
* 返回圖中的頂點數
*/
int V();
/**
* 返回圖中的邊數
*/
int E();
/**
* 向圖中添加一條邊
* @param v 頂點 v
* @param w 頂點 w
*/
void addEdge(int v, int w);
/**
* 返回所有相鄰頂點
* @param v 頂點 v
* @return 所有相鄰頂點
*/
Iterable<Integer> adj(int v);
}用矩陣表示圖對研究圖的性質及應用常常是比較方便的,對于各種圖有各種矩陣表示方式,比如權矩陣和鄰接矩陣,這里我們只關注鄰接矩陣。它的定義為:
對于圖G=(V,E),|V|=n,構造一個矩陣 A=(aij)n×n,其中:

則稱矩陣A為圖G的鄰接矩陣。
由定義可知,我們可以使用一個二維的布爾數組 A 來實現鄰接矩陣,當 A[i][j] = true 時說明頂點 i 和 j 相鄰。
對于 n個頂點的圖 G,鄰接矩陣需要消耗的空間為 n2個布爾值的大小,對于稀疏圖來說會造成很大的浪費,當頂點數很大時所消耗的空間會是個天文數字。同時當圖比較特殊,存在自環以及平行邊時,鄰接矩陣的表示方式是無能為力的。《算法》中給出了存在這兩種情況的圖:
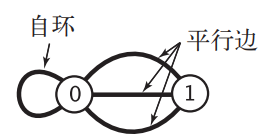
對于無向圖,我們可以實現一個類 Edge,里面只用兩個實例變量用來存儲兩個頂點 u和 v,接著在一個數組里面保存所有 Edge 即可。這樣做有一個很大的問題,就是在獲取頂點 v的所有相鄰頂點時必須遍歷整個數組才能得到,時間復雜度是O(|E|),由于獲取相鄰頂點是很常用的操作,所以這種表示方式也不太行。
如果我們把頂點表示為一個整數,取值范圍為0∼|V|−1,那么就可以用一個長度為|V| 的數組的索引表示每一個頂點,然后將每一個數組元素設置為一個鏈表,上面掛載著索引所代表的的頂點相鄰的其他頂點。圖一所示的無向圖可以用下圖所示的鄰接表數組表示出來:
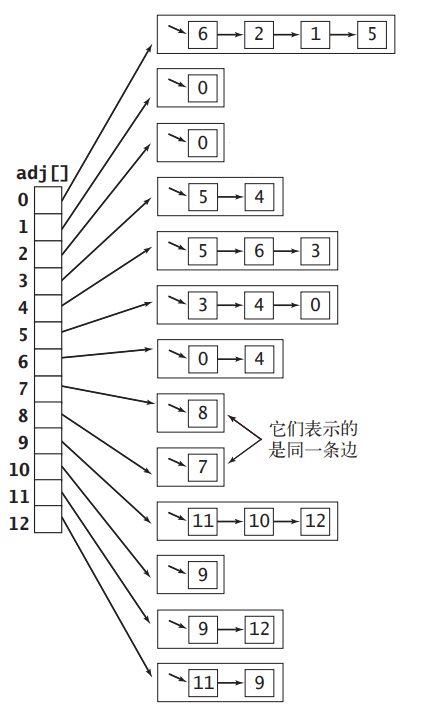
使用鄰接表實現無向圖的代碼如下所示,由于鄰接表數組中的每個鏈表都會保存與頂點相鄰的頂點,所以將邊添加到圖中時需要對數組中的兩個鏈表進行添加節點的操作:
package com.zhiyiyo.graph;
import com.zhiyiyo.collection.stack.LinkStack;
/**
* 使用鄰接表實現的無向圖
*/
public class LinkGraph implements Graph {
private final int V;
private int E;
private LinkStack<Integer>[] adj;
public LinkGraph(int V) {
this.V = V;
adj = (LinkStack<Integer>[]) new LinkStack[V];
for (int i = 0; i < V; i++) {
adj[i] = new LinkStack<>();
}
}
@Override
public int V() {
return V;
}
@Override
public int E() {
return E;
}
@Override
public void addEdge(int v, int w) {
adj[v].push(w);
adj[w].push(v);
E++;
}
@Override
public Iterable<Integer> adj(int v) {
return adj[v];
}
}這里用到的棧代碼如下所示,棧的實現不是這篇博客的重點,所以這里不做過多解釋:
package com.zhiyiyo.collection.stack;
import java.util.EmptyStackException;
import java.util.Iterator;
/**
* 使用鏈表實現的堆棧
*/
public class LinkStack<T> {
private int N;
private Node first;
public void push(T item) {
first = new Node(item, first);
N++;
}
public T pop() throws EmptyStackException {
if (N == 0) {
throw new EmptyStackException();
}
T item = first.item;
first = first.next;
N--;
return item;
}
public int size() {
return N;
}
public boolean isEmpty() {
return N == 0;
}
public Iterator<T> iterator() {
return new ReverseIterator();
}
private class Node {
T item;
Node next;
public Node() {
}
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
private class ReverseIterator implements Iterator<T> {
private Node node = first;
@Override
public boolean hasNext() {
return node != null;
}
@Override
public T next() {
T item = node.item;
node = node.next;
return item;
}
@Override
public void remove() {
}
}
}給定下面一幅圖,現在要求找到每個頂點到頂點 0 的路徑,該如何實現?或者簡單點,給定頂點 0 和 4,要求判斷從頂點 0 開始走,能否到達頂點 4,該如何實現?這就要用到兩種圖的遍歷方式:深度優先搜索和廣度優先搜索。
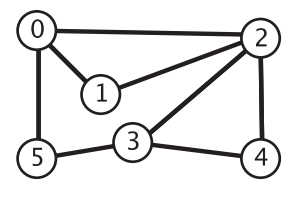
在介紹這兩種遍歷方式之前,先給出解決上述問題需要實現的 API:
package com.zhiyiyo.graph;
public interface Search {
/**
* 起點 s 和 頂點 v 之間是否連通
* @param v 頂點 v
* @return 是否連通
*/
boolean connected(int v);
/**
* 返回與頂點 s 相連通的頂點個數(包括 s)
*/
int count();
/**
* 是否存在從起點 s 到頂點 v 的路徑
* @param v 頂點 v
* @return 是否存在路徑
*/
boolean hasPathTo(int v);
/**
* 從起點 s 到頂點 v 的路徑,不存在則返回 null
* @param v 頂點 v
* @return 路徑
*/
Iterable<Integer> pathTo(int v);
}深度優先搜索的思想類似樹的先序遍歷。我們從頂點 0 開始,將它的相鄰頂點 2、1、5 加到棧中。接著彈出棧頂的頂點 2,將它相鄰的頂點 0、1、3、4 添加到棧中,但是寫到這你就會發現一個問題:頂點 0 和 1明明已經在棧中了,如果還把他們加到棧中,那這個棧豈不是永遠不會變回空。所以還需要維護一個數組 boolean[] marked,當我們將一個頂點 i 添加到棧中時,就將 marked[i] 置為 true,這樣下次要想將頂點 i 加入棧中時,就得先檢查一個 marked[i] 是否為 true,如果為 true 就不用再添加了。重復棧頂節點的彈出和節點相鄰節點的入棧操作,直到棧為空,我們就完成了頂點 0 可達的所有頂點的遍歷。
為了記錄每個頂點到頂點 0 的路徑,我們還需要一個數組 int[] edgeTo。每當我們訪問到頂點 u 并將其一個相鄰頂點 i 壓入棧中時,就將 edgeTo[i] 設置為 u,說明要想從頂點i 到達頂點 0,需要先回退頂點 u,接著再從頂點 edgeTo[u] 處獲取下一步要回退的頂點直至找到頂點 0。
package com.zhiyiyo.graph;
import com.zhiyiyo.collection.stack.LinkStack;
import com.zhiyiyo.collection.stack.Stack;
public class DepthFirstSearch implements Search {
private boolean[] marked;
private int[] edgeTo;
private Graph graph;
private int s;
private int N;
public DepthFirstSearch(Graph graph, int s) {
this.graph = graph;
this.s = s;
marked = new boolean[graph.V()];
edgeTo = new int[graph.V()];
dfs();
}
/**
* 遞歸實現的深度優先搜索
*
* @param v 頂點 v
*/
private void dfs(int v) {
marked[v] = true;
N++;
for (int i : graph.adj(v)) {
if (!marked[i]) {
edgeTo[i] = v;
dfs(i);
}
}
}
/**
* 堆棧實現的深度優先搜索
*/
private void dfs() {
Stack<Integer> vertexes = new LinkStack<>();
vertexes.push(s);
marked[s] = true;
while (!vertexes.isEmpty()) {
Integer v = vertexes.pop();
N++;
// 將所有相鄰頂點加到堆棧中
for (Integer i : graph.adj(v)) {
if (!marked[i]) {
edgeTo[i] = v;
marked[i] = true;
vertexes.push(i);
}
}
}
}
@Override
public boolean connected(int v) {
return marked[v];
}
@Override
public int count() {
return N;
}
@Override
public boolean hasPathTo(int v) {
return connected(v);
}
@Override
public Iterable<Integer> pathTo(int v) {
if (!hasPathTo(v)) return null;
Stack<Integer> path = new LinkStack<>();
int vertex = v;
while (vertex != s) {
path.push(vertex);
vertex = edgeTo[vertex];
}
path.push(s);
return path;
}
}廣度優先搜索的思想類似樹的層序遍歷。與深度優先搜索不同,從頂點 0 出發,廣度優先搜索會先處理完所有與頂點 0 相鄰的頂點 2、1、5 后,才會接著處理頂點 2、1、5 的相鄰頂點。這個搜索過程就是一圈一圈往外擴展、越走越遠的過程,所以可以用來獲取頂點 0 到其他節點的最短路徑。只要將深度優先搜索中的堆換成隊列,就能實現廣度優先搜索:
package com.zhiyiyo.graph;
import com.zhiyiyo.collection.queue.LinkQueue;
public class BreadthFirstSearch implements Search {
private boolean[] marked;
private int[] edgeTo;
private Graph graph;
private int s;
private int N;
public BreadthFirstSearch(Graph graph, int s) {
this.graph = graph;
this.s = s;
marked = new boolean[graph.V()];
edgeTo = new int[graph.V()];
bfs();
}
private void bfs() {
LinkQueue<Integer> queue = new LinkQueue<>();
marked[s] = true;
queue.enqueue(s);
while (!queue.isEmpty()) {
int v = queue.dequeue();
N++;
for (Integer i : graph.adj(v)) {
if (!marked[i]) {
edgeTo[i] = v;
marked[i] = true;
queue.enqueue(i);
}
}
}
}
}隊列的實現代碼如下:
package com.zhiyiyo.collection.queue;
import java.util.EmptyStackException;
public class LinkQueue<T> {
private int N;
private Node first;
private Node last;
public void enqueue(T item) {
Node node = new Node(item, null);
if (++N == 1) {
first = node;
} else {
last.next = node;
}
last = node;
}
public T dequeue() throws EmptyStackException {
if (N == 0) {
throw new EmptyStackException();
}
T item = first.item;
first = first.next;
if (--N == 0) {
last = null;
}
return item;
}
public int size() {
return N;
}
public boolean isEmpty() {
return N == 0;
}
private class Node {
T item;
Node next;
public Node() {
}
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}關于“Java這么實現無向圖”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“Java這么實現無向圖”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。