python如何實現貝葉斯推斷

這篇文章給大家分享的是有關python如何實現貝葉斯推斷的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

1. 前言

        貝葉斯推斷的python實現例，并展現了基于標量運算的實現和基于numpy的矩陣運算的實現之間的差別。

2. 問題描述

本問題例取自于Ref1-Chapter1.

問題描述：假設有一個制作燈泡的機器。你想知道機器是正常工作還是有問題。為了得到答案你可以測試每一個燈泡，但是燈泡數量很多，每一個都測試在實際生產過程中可能是無法承受的。使用貝葉斯推斷，你可以基于少量樣本（比如說抽檢結果）來估計機器是否在正常地工作（in probabilistic way）。

構建貝葉斯推斷時，首先需要兩個要素:

(1) 先驗分布

(2) 似然率

先驗分布是我們關于機器工作狀態的初始信念。首先我們確定第一個刻畫機器工作狀態的隨機變量，記為M。這個隨機變量有兩個工作狀態：{working, broken}，以下簡寫成{w, br}(縮寫成br是為了與下面的Bad縮寫成b區分開來)。作為初始信念，我們相信機器是好的，是可以正常工作的，定義先驗分布如下：

P(M=working) = 0.99

P(M=broken ) = 0.01

這表明我們對于機器正常工作的信念度很高，有99%的概率能夠正常工作。

第二個隨機變量是L，表示機器生產的燈泡的工作狀態。燈泡可能是好，也可能是壞的，包含兩個狀態：{good, bad}，以下簡寫成{g,b}，注意br與b的區別。

我們需要基于機器工作狀態給出L的先驗分布，也就是條件概率P(L|M)，在貝葉斯公式中它代表似然概率(likelihood)。

定義這個似然概率分布（由于M和L各有兩種狀態，所以一共包含4個條件概率）如下：

P(L=Good|M=w) = 0.99

P(L=Bad |M=w) = 0.01

P(L=Good|M=br ) = 0.6

P(L=Bad |M=br ) = 0.4

以上似然概率表明，在機器正常時我們相信每生成100個燈泡只會有一個壞的，而機器不正常時也不是所有燈泡都是壞的，而是有40%會是壞的。為了實現的方便，可以寫成如下的矩陣形式：

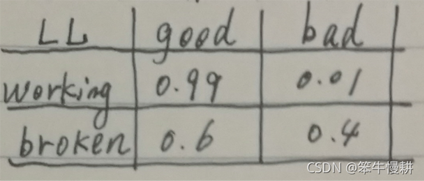
        現在，我們已經完整地刻畫了貝葉斯模型，可以用它來做一些神奇的估計和預測的工作了。

        我們的輸入是一些燈泡的抽檢結果。假設我們抽檢了十個燈泡其抽檢結果如下：

   {bad, good, good, good, good, good, good, good, good, good}

        讓我們來看看基于貝葉斯推斷的我們對于機器工作狀態的信念（后驗概率）如何變化。

3. 貝葉斯規則

        貝葉斯推斷規則以貝葉斯公式的形式表示為：

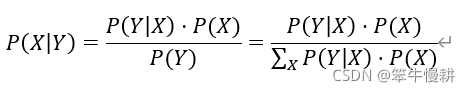
         具體映射到本問題中可以表達如下：

         貝

葉斯推斷的優先在于可以以在線（online）的方式進行，即觀測數據可以一個一個地到來，每次受到一個新的觀測數據，就進行一次基于貝葉斯公式的后驗概率的計算更新，而更新后的后驗概率又作為下一貝葉斯推斷的先驗概率使用。因此在線的貝葉斯推斷的基本處理流程如下所示：

4. Bayes engine: scalar implementation

        首先，我們以標量運算的方式寫一個函數來進行bayes推斷處理。

        prior以向量的形式存儲先驗概率分布，prior[0]表示P(M=working)，prior[1]表示P(M=broken)。

        likelihood以矩陣的形式方式存儲似然概率分布。其中第1行表示P(L/M=working)，第2行表示P(L/M=broken).

        在本例中，當輸入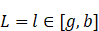 時，evidence的計算式（注意evidence是依賴于輸入的觀測數據的）是:

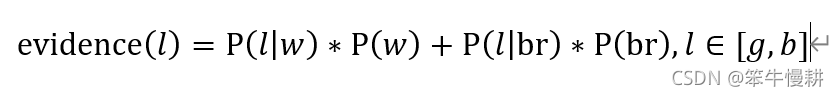
        注意，當我寫P(w)其實是表示P(M=w)，而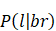 其實是表示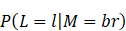 ，余者類推。根據上下文，這些應該不會導致混淆。

        第一個函數的代碼如下：

def bayes_scalar(prior, likelihood, data):
    """
    Bayesian inference function example.
    Parameters
    ----------
    prior : float, 1-D vector
        prior information, P(X).
    likelihood : float 2-D matrix
        likelihood function, P(Y|X).
    data : List of strings. Value: 'Good','Bad'
        Observed data samples sequence
    Returns
    -------
    posterior : float
        P(X,Y), posterior sequence.
    """
    
    posterior = np.zeros((len(data)+1,2))
    posterior[0,:] = prior  # Not used in computation, just for the later plotting
 
    for k,L in enumerate(data):
        if L == 'good':
            L_value = 0
        else:
            L_value = 1
        #print(L, L_value, likelihood[:,L_value])
 
        evidence      = likelihood[0,L_value] * prior[0] + likelihood[1,L_value] * prior[1]
        LL0_prior_prod= likelihood[0,L_value] * prior[0]                
        posterior[k+1,0]  = LL0_prior_prod / evidence
 
        LL1_prior_prod= likelihood[1,L_value] * prior[1]        
        posterior[k+1,1]  = LL1_prior_prod / evidence
        
        prior = posterior[k+1,:] # Using the calculated posterior at this step as the prior for the next step
                
    return posterior

 5. Bayes engine: vectorization

        我們注意到，evidence的計算可以表示成兩個向量的點積，如下所示。

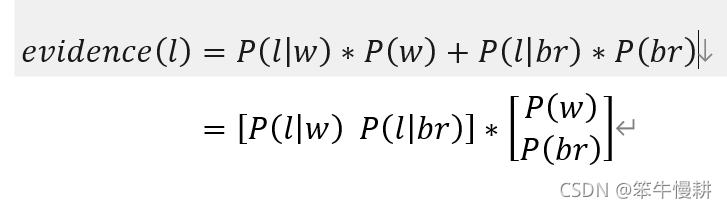
        這樣就非常方便用numpy來實現了。本例中每個隨機變量只有兩種取值，在復雜的情況下，每個隨機變量有很多種取值時，有效利用向量或矩陣的運算是簡潔的運算實現的必不可缺的要素。以上這兩個向量的點積可以用numpy.dot()來實現。

        另外，likelihood和prior的乘積是分別針對M的兩種狀態進行計算（注意，我們需要針對M的兩種不同狀態分別計算posterior），不是用向量的點積進行計算，而是一種element-wise multiplication，可以用numpy.multiply()進行計算。所以在vectorization版本中貝葉斯更新處理削減為兩條語句，與上面的scalar版本相比顯得非常優雅簡潔（好吧，也許這個簡單例子中還顯不出那么明顯的優勢，但是隨著問題的復雜度的增加，這種優勢就會越來越明顯了。）

         由此我們得到向量化處理的函數如下： 

def bayes_vector(prior, likelihood, data):
    """
    Bayesian inference function example.
    Parameters
    ----------
    prior : float, 1-D vector
        prior information, P(X).
    likelihood : float 2-D matrix
        likelihood function, P(Y|X).
    data : List of strings. Value: 'Good','Bad'
        Observed data samples sequence
    Returns
    -------
    posterior : float
        P(X,Y), posterior sequence.
    """
    
    posterior = np.zeros((len(data)+1,2))
    posterior[0,:] = prior  # Not used in computation, just for the later plotting
 
    for k,L in enumerate(data):
        if L == 'good':
            L_value = 0
        else:
            L_value = 1
        #print(L, L_value, likelihood[:,L_value])
 
        evidence          = np.dot(likelihood[:,L_value], prior[:])
        posterior[k+1,:]  = np.multiply(likelihood[:,L_value],prior)/evidence
 
        prior = posterior[k+1,:] # Using the calculated posterior at this step as the prior for the next step
        
    return posterior

6. 測試

        讓我們來看看利用以上函數對我們的觀測數據進行處理，后驗概率將會如何變化。

import numpy as np
import matplotlib.pyplot as plt
 
prior      = np.array([0.99,0.01])
likelihood = np.array([[0.99,0.01],[0.6,0.4]])
data       = ['bad','good','good','good','good','good','good','good']        
 
posterior1 = bayes_scalar(prior,likelihood,data)
posterior2 = bayes_vector(prior,likelihood,data)
 
if np.allclose(posterior1,posterior2):
    print('posterior1 and posterior2 are identical!')
 
fig, ax = plt.subplots()
ax.plot(posterior1[:,0])
ax.plot(posterior1[:,1])
ax.grid()
# fig.suptitle('Poeterior curve vs observed data')
ax.set_title('Posterior curve vs observed data')
plt.show()

        運行以上代碼可以得到后驗概率的變化如下圖所示（注意第一個點是prior）：

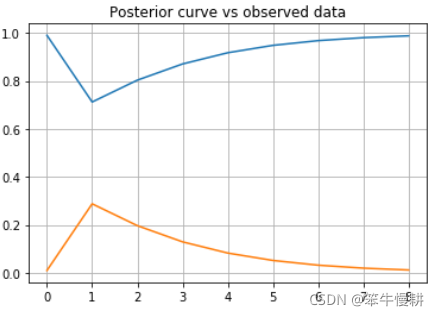
         當然以上代碼也順便驗證了一下兩個版本的bayes函數是完全等價的。

感謝各位的閱讀！關于“python如何實現貝葉斯推斷”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！