您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“python模擬樸素貝葉斯程序舉例分析”,在日常操作中,相信很多人在python模擬樸素貝葉斯程序舉例分析問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”python模擬樸素貝葉斯程序舉例分析”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
樸素貝葉斯思想:運用了條件概率公式P(Y,X) = P(Y)P(X|Y)。由樣本分別求得P(Y)和P(X|Y),進而估計出在X條件下Y的概率。不同Y對應的概率的最大值就是我們想要的X的分類。換句話說,我們想要知道X的分類,那么通過樣本求出不同類別(即不同Y)時的P(Y)和P(X|Y),然后計算X發生條件下,可能類別Y的概率,最大的概率就是我們預測的概率。
注意,通常X對應很多分量,X=(X1,X2,······)。這時候貝葉斯估計假設:用于分類的特征在類確定的條件下是條件獨立的。所以上面的P(X|Y)計算公式為:
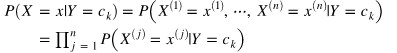
樸素貝葉斯代碼的實現
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
class NaiveBayes:
def __init__(self):
self.model = None
# 數學期望
@staticmethod
def mean(X):
return sum(X) / float(len(X))
# 標準差
def stdev(self, X):
avg = self.mean(X)
return math.sqrt(sum([pow(x - avg, 2) for x in X]) / float(len(X)))
# 概率密度函數
def gaussian_probability(self, x, mean, stdev):
exponent = math.exp(-(math.pow(x - mean, 2) /
(2 * math.pow(stdev, 2))))
return (1 / (math.sqrt(2 * math.pi) * stdev)) * exponent
# 分類別求出數學期望和標準差
def summarize(self, train_data):
a = list(zip(*train_data))
summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
# *train_data將train_data拆分成n個一維數組
# 再將這個一維數組壓縮在一起。
# 注意:這里壓縮的時候,一共壓縮成了四個一維數組,
# 即每個原數組的第一維進行壓縮,每個原數組的第二維進行壓縮······
# 然后分別對四個一維數組進行求均值和標準差,即對四個特征求響應的數字特征
return summaries
# 處理X_train,y_train
def fit(self, X, y):
labels = list(set(y)) # set將y刪除掉重復的,list將set結果轉成列表。這里labels=[0.0, 1.0]
data = {label: [] for label in labels} # 轉成字典。輸出{0.0: [], 1.0: []}
for f, label in zip(X, y):
data[label].append(f) # 將上面的字典添加屬于這個類的值。即類型是label的f
self.model = {
label: self.summarize(value) for label, value in data.items()
# 從上述字典中,一個label及其對應的屬于這個label的數據,進行數字特征的計算
# 結果格式: {0:[(均值, 標準差), (均值, 標準差), (均值, 標準差), (均值, 標準差)],
# 1: [(均值, 標準差), (均值, 標準差), (均值, 標準差), (均值, 標準差)]}
# 0后邊的四項分別對應:label是0的樣品的四個特征的均值和標準差
}
return 'gaussianNB train done!'
# 計算概率
def calculate_probabilities(self, input_data):
probabilities = {}
for label, value in self.model.items():
probabilities[label] = 1
for i in range(len(value)):
mean, stdev = value[i]
probabilities[label] *= self.gaussian_probability(
input_data[i], mean, stdev)
return probabilities
# 類別
def predict(self, X_test):
label = sorted(
self.calculate_probabilities(X_test).items(),
key=lambda x: x[-1])[-1][0]
return label
def score(self, X_test, y_test):
right = 0
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right += 1
if right / float(len(X_test))==1.0:
return "perfect!"
else:
return right / float(len(X_test))
def create_data():
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, :])
return data[:, :-1], data[:, -1], df
X, y, DF = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
model = NaiveBayes()
model.fit(X_train, y_train)
print(model.score(X_test, y_test))結果比較理想
直接運用sklearn中現有的包進行模擬
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import BernoulliNB, MultinomialNB # 伯努利模型和多項式模型
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = [
'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
]
data = np.array(df.iloc[:100, :])
return data[:, :-1], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
clf = GaussianNB()
clf.fit(X_train, y_train)
print("GaussianNB:")
print(clf.score(X_test, y_test))
print(clf.predict([[4.4, 3.2, 1.3, 0.2]]))
clf2 = BernoulliNB()
clf2.fit(X_train, y_train)
print("\nBernoulliNB:")
print(clf2.score(X_test, y_test))
print(clf2.predict([[4.4, 3.2, 1.3, 0.2]]))
clf3 = MultinomialNB()
clf3.fit(X_train, y_train)
print("\nMultinomialNB:")
print(clf3.score(X_test, y_test))
print(clf3.predict([[4.4, 3.2, 1.3, 0.2]]))輸出結果
GaussianNB: 1.0 [0.] BernoulliNB: 0.4666666666666667 [1.] MultinomialNB: 1.0 [0.]
可以看到,高斯模型和多項式模型較好的進行了預測,但是伯努利模型預測結果較差。
原因:數據不符合伯努利分布。
到此,關于“python模擬樸素貝葉斯程序舉例分析”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。