LRU算法的實現原理

這篇文章主要講解了“LRU算法的實現原理”，文中的講解內容簡單清晰，易于學習與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學習“LRU算法的實現原理”吧！

前言

我們常用緩存提升數據查詢速度，由于緩存容量有限，當緩存容量到達上限，就需要刪除部分數據挪出空間，這樣新數據才可以添加進來。緩存數據不能隨機刪除，一般情況下我們需要根據某種算法刪除緩存數據。常用淘汰算法有 LRU,LFU,FIFO,這篇文章我們聊聊 LRU 算法。

LRU 簡介

LRU 是 Least Recently Used 的縮寫，這種算法認為最近使用的數據是熱門數據，下一次很大概率將會再次被使用。而最近很少被使用的數據，很大概率下一次不再用到。當緩存容量的滿時候，優先淘汰最近很少使用的數據。

假設現在緩存內部數據如圖所示：

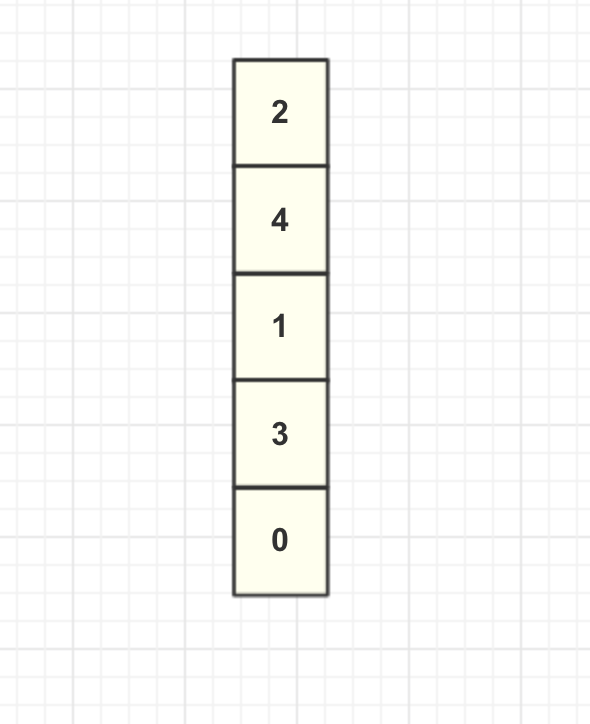
這里我們將列表第一個節點稱為頭結點，最后一個節點為尾結點。

當調用緩存獲取 key=1 的數據，LRU 算法需要將 1 這個節點移動到頭結點，其余節點不變，如圖所示。

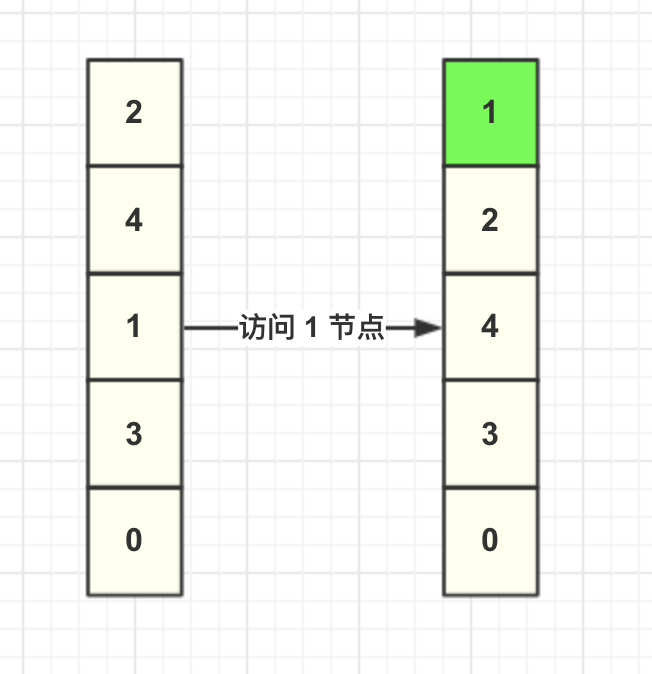
然后我們插入一個 key=8 節點，此時緩存容量到達上限，所以加入之前需要先刪除數據。由于每次查詢都會將數據移動到頭結點，未被查詢的數據就將會下沉到尾部節點，尾部的數據就可以認為是最少被訪問的數據，所以刪除尾結點的數據。

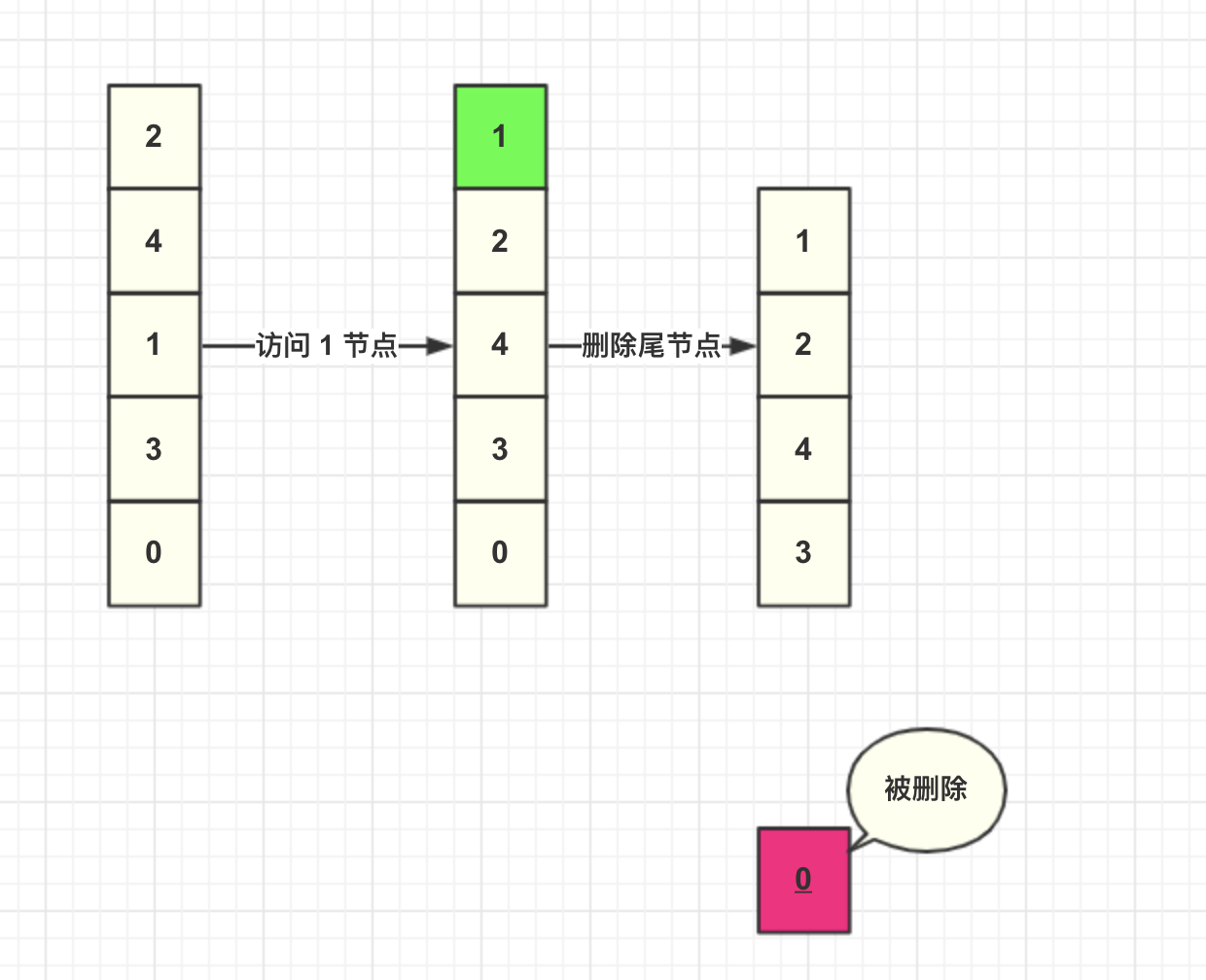
然后我們直接將數據添加到頭結點。

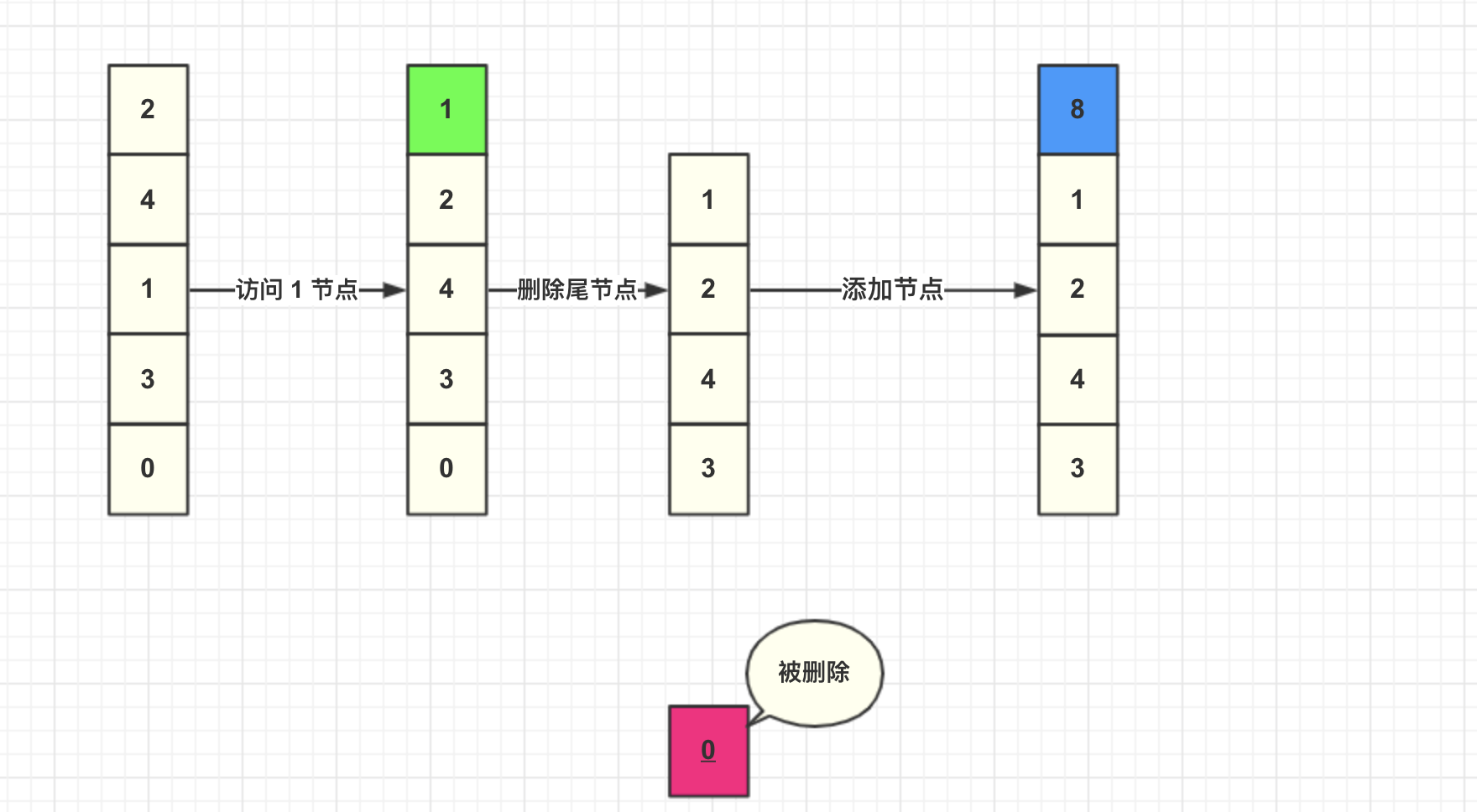
這里總結一下 LRU 算法具體步驟：

• 新數據直接插入到列表頭部

• 緩存數據被命中，將數據移動到列表頭部

• 緩存已滿的時候，移除列表尾部數據。

LRU 算法實現

上面例子中可以看到，LRU 算法需要添加頭節點，刪除尾結點。而鏈表添加節點/刪除節點時間復雜度 O(1)，非常適合當做存儲緩存數據容器。但是不能使用普通的單向鏈表，單向鏈表有幾點劣勢:

1. 每次獲取任意節點數據，都需要從頭結點遍歷下去，這就導致獲取節點復雜度為 O(N)。

2. 移動中間節點到頭結點，我們需要知道中間節點前一個節點的信息，單向鏈表就不得不再次遍歷獲取信息。

針對以上問題，可以結合其他數據結構解決。

使用散列表存儲節點，獲取節點的復雜度將會降低為 O(1)。節點移動問題可以在節點中再增加前驅指針，記錄上一個節點信息，這樣鏈表就從單向鏈表變成了雙向鏈表。

綜上使用雙向鏈表加散列表結合體，數據結構如圖所示:

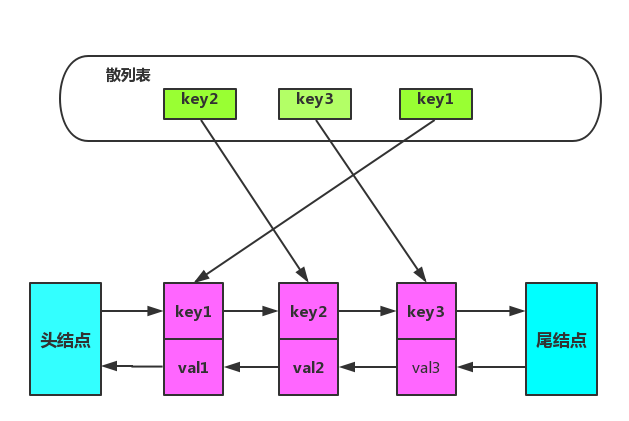
在雙向鏈表中特意增加兩個『哨兵』節點，不用來存儲任何數據。使用哨兵節點，增加/刪除節點的時候就可以不用考慮邊界節點不存在情況，簡化編程難度，降低代碼復雜度。

LRU 算法實現代碼如下，為了簡化 key ，val 都認為 int 類型。

public class LRUCache {

    Entry head, tail;
    int capacity;
    int size;
    Map<Integer, Entry> cache;


    public LRUCache(int capacity) {
        this.capacity = capacity;
        // 初始化鏈表
        initLinkedList();
        size = 0;
        cache = new HashMap<>(capacity + 2);
    }

    /**
     * 如果節點不存在，返回 -1.如果存在，將節點移動到頭結點，并返回節點的數據。
     *
     * @param key
     * @return
     */
    public int get(int key) {
        Entry node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // 存在移動節點
        moveToHead(node);
        return node.value;
    }

    /**
     * 將節點加入到頭結點，如果容量已滿，將會刪除尾結點
     *
     * @param key
     * @param value
     */
    public void put(int key, int value) {
        Entry node = cache.get(key);
        if (node != null) {
            node.value = value;
            moveToHead(node);
            return;
        }
        // 不存在。先加進去，再移除尾結點
        // 此時容量已滿 刪除尾結點
        if (size == capacity) {
            Entry lastNode = tail.pre;
            deleteNode(lastNode);
            cache.remove(lastNode.key);
            size--;
        }
        // 加入頭結點

        Entry newNode = new Entry();
        newNode.key = key;
        newNode.value = value;
        addNode(newNode);
        cache.put(key, newNode);
        size++;

    }

    private void moveToHead(Entry node) {
        // 首先刪除原來節點的關系
        deleteNode(node);
        addNode(node);
    }

    private void addNode(Entry node) {
        head.next.pre = node;
        node.next = head.next;

        node.pre = head;
        head.next = node;
    }

    private void deleteNode(Entry node) {
        node.pre.next = node.next;
        node.next.pre = node.pre;
    }


    public static class Entry {
        public Entry pre;
        public Entry next;
        public int key;
        public int value;

        public Entry(int key, int value) {
            this.key = key;
            this.value = value;
        }

        public Entry() {
        }
    }

    private void initLinkedList() {
        head = new Entry();
        tail = new Entry();

        head.next = tail;
        tail.pre = head;

    }

    public static void main(String[] args) {

        LRUCache cache = new LRUCache(2);

        cache.put(1, 1);
        cache.put(2, 2);
        System.out.println(cache.get(1));
        cache.put(3, 3);
        System.out.println(cache.get(2));

    }
}

LRU 算法分析

緩存命中率是緩存系統的非常重要指標，如果緩存系統的緩存命中率過低，將會導致查詢回流到數據庫，導致數據庫的壓力升高。

結合以上分析 LRU 算法優缺點。

LRU 算法優勢在于算法實現難度不大，對于對于熱點數據， LRU 效率會很好。

LRU 算法劣勢在于對于偶發的批量操作，比如說批量查詢歷史數據，就有可能使緩存中熱門數據被這些歷史數據替換，造成緩存污染，導致緩存命中率下降，減慢了正常數據查詢。

LRU 算法改進方案

以下方案來源與 MySQL InnoDB LRU 改進算法

將鏈表拆分成兩部分，分為熱數據區，與冷數據區，如圖所示。

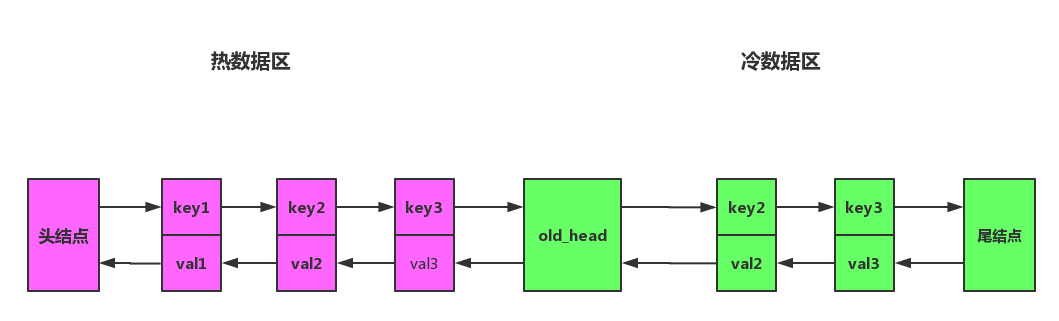
改進之后算法流程將會變成下面一樣:

1. 訪問數據如果位于熱數據區，與之前 LRU 算法一樣，移動到熱數據區的頭結點。

2. 插入數據時，若緩存已滿，淘汰尾結點的數據。然后將數據插入冷數據區的頭結點。

3. 處于冷數據區的數據每次被訪問需要做如下判斷：

• 若該數據已在緩存中超過指定時間，比如說 1 s，則移動到熱數據區的頭結點。

• 若該數據存在在時間小于指定的時間，則位置保持不變。

對于偶發的批量查詢，數據僅僅只會落入冷數據區，然后很快就會被淘汰出去。熱門數據區的數據將不會受到影響，這樣就解決了 LRU 算法緩存命中率下降的問題。

感謝各位的閱讀，以上就是“LRU算法的實現原理”的內容了，經過本文的學習后，相信大家對LRU算法的實現原理這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是億速云，小編將為大家推送更多相關知識點的文章，歡迎關注！