c++字符串匹配的知識點有哪些

今天小編給大家分享一下c++字符串匹配的知識點有哪些的相關知識點，內容詳細，邏輯清晰，相信大部分人都還太了解這方面的知識，所以分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后有所收獲，下面我們一起來了解一下吧。

字符串匹配

我們在字符串 A 中查找字符串 B，那字符串 A 就是主串，字符串 B 就是模式串。我們把主串的長度記作 n，模式串的長度記作 m。因為我們是在主串中查找模式串，所以 n>m。

單模式串匹配的算法：也就是一個串跟一個串進行匹配

BF 算法中的 BF 是 Brute Force 的縮寫，中文叫作暴力匹配算法，也叫樸素匹配算法。我們在主串中，檢查起始位置分別是 0、1、2…n-m 且長度為 m 的 n-m+1 個子串，看有沒有跟模式串匹配的。BF 算法的時間復雜度很高，是 O(n*m)

實際的開發中，它卻是一個比較常用的字符串匹配算法，絕大部分情況下，樸素的字符串匹配算法就夠用了。

• 實際的軟件開發中，大部分情況下，模式串和主串的長度都不會太長。

• 樸素字符串匹配算法思想簡單，代碼實現也非常簡單。滿足KISS（Keep it Simple and Stupid）設計原則

•  

RK 算法的全稱叫 Rabin-Karp 算法，是由它的兩位發明者 Rabin 和 Karp 的名字來命名的。思路是這樣的：我們通過哈希算法對主串中的 n-m+1 個子串分別求哈希值，然后逐個與模式串的哈希值比較大小。如果某個子串的哈希值與模式串相等，那就說明對應的子串和模式串匹配了（無哈希沖突）。如果有哈希沖突，再對比一下子串和模式串本身。

RK 算法的效率要比 BF 算法高，RK 算法整體的時間復雜度就是 O(n)。不過這樣的效率取決于哈希算法的設計方法，如果存在沖突的情況下，時間復雜度可能會退化。極端情況下，哈希算法大量沖突，時間復雜度就退化為 O(n*m)。

要求：設計hash算法。找出兩個子串 s[i-1] 和 s[i]關系（其實就是abcde, bad表示相同子串， a與e的關系）。

BM （Boyer-Moore）算法:它的性能是著名的KMP 算法的 3 到 4 倍。當遇到不匹配的字符時，找規律，將模式串往后多滑動幾位。

BM 算法包含兩部分，分別是壞字符規則（bad character rule）和好后綴規則（good suffix shift）。

壞字符規則：從模式串的末尾往前倒著匹配，當我們發現某個字符沒法匹配的時候。我們把這個沒有匹配的字符叫作壞字符（主串中的字符）

當發生不匹配的時候，我們把壞字符對應的模式串中的字符下標記作 si。如果壞字符在模式串中存在，我們把這個壞字符在模式串中(最靠后的一個)的下標記作 xi。如果不存在，我們把 xi 記作 -1。那模式串往后移動的位數就等于 si-xi。（注意，我這里說的下標，都是字符在模式串的下標）。

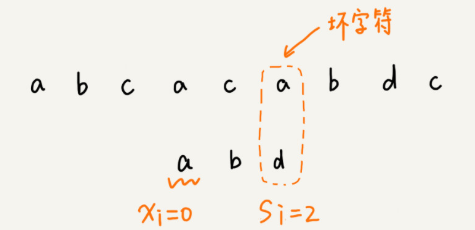
需要bc數組，記錄模式串所有字符位置。

缺點：單純使用壞字符規則還是不夠的。因為根據 si-xi 計算出來的移動位數，有可能是負數，比如主串是 aaaaaaaaaaaaaaaa，模式串是 baaa。

好后綴規則：

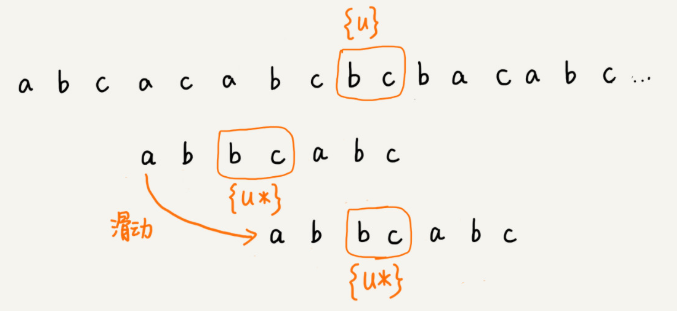
• 當好后綴{u}在模式串中查找，如果找到了另一個跟{u}相匹配的子串{u*}，那我們就將模式串滑動到子串{u*}與主串中{u}對齊的位置。

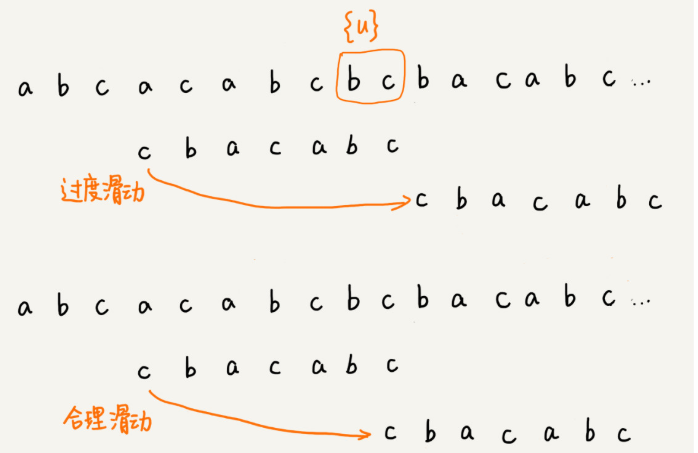
• 當好后綴{u}在模式串中查找，不存在另一個跟{u}相匹配的子串{u*}，不能過度滑動到主串中{u}的后面。而是，從好后綴的后綴子串中，找一個最長的并且能跟模式串的前綴子串匹配的，假設是{v}，然后將模式串滑動到如圖所示的位置。

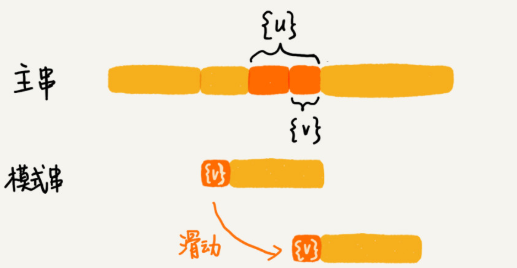
abc 的后綴子串就包括 c, bc。 abc 的前綴子串有 a，ab。

算法實現：

壞字符規則實現

• 利用散列表存儲模式串每個字符位置下標，相同字符，記錄最后出現下標

• 起始下標i,模式串從后往前匹配，遇到壞字符。找到壞字符對應模式串中的下標是si, 找到壞字符在模式串中最后出現位置xi (利用散列表，key=字符，value=下標，沒有計為-1），

     計算滑動i = i + (j - bc[(int)a[i+j]]);

好后綴規則實現（壞字符不在模式串m中最后一個位置）

• 預處理模式串，用數組存。每個數組元素記錄另一個可匹配后綴子串的位置。如下圖suffix[1],表示長度為1的子串，最后匹配的子串下標為2.

• 除了 suffix 數組之外，我們還需要另外一個 boolean 類型的 prefix 數組，來記錄模式串的后綴子串是否能匹配模式串的前綴子串。

如何來計算并填充這兩個數組的值？

拿下標從 0 到 i 的子串（i 可以是 0 到 m-2）與整個模式串，求公共后綴子串。如果公共后綴子串的長度是 k，那我們就記錄 suffix[k]=j（j 表示公共后綴子串的起始下標）。如果 j 等于 0，也就是說，公共后綴子串也是模式串的前綴子串，我們就記錄 prefix[k]=true。

private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {  

    // 初始化  

    for (int i = 0; i < m; ++i) {  

        suffix[i] = -1;  

        prefix[i] = false;  

    }  

    // abcde的好后綴是bcde,所以要減去一  

    // 前綴串b[0,m-2]與后綴串b[1,m-1]求公共后綴子串,以b[m-1] 為比較  

    // 比如cab 與b 求后綴子串  

    for (int i = 0; i < m - 1; i++) {  

        int j = i;  

        int k = 0;  

        while (j >= 0 && b[j] == b[m - 1 - k]) {  

            ++k;  

            suffix[k] = j;  

            --j;  

        }  

        if (j == -1) {  

            prefix[k] = true;  

        }  

    }  

}  

abc 的后綴子串就包括 c, bc。后綴子串必須有最后一個值。 abc 的前綴子串有 a，ab。前綴子串必須有第一個值

求前綴子串與后綴子串的公共后綴子串，并記錄前綴子串是否可完全匹配。

• 通過好后綴長度k，判斷，是否存在另一匹配后綴。suffix[k]!=-1, 滑動j-x+1位。

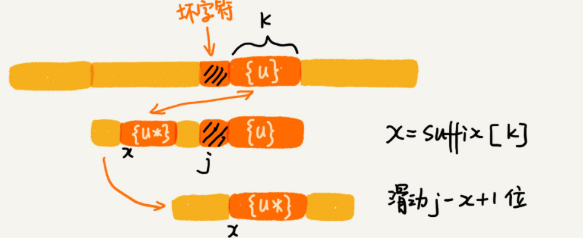
• 好后綴{u}, 不在模式串中存在時。就需要找，后綴子串中是否有匹配的前綴子串。j為壞字符下標，循環找（r<=m-1）好后綴的后綴子串為b[r,m-1],r=j+2（是因為求好后綴的后綴子串） ，長度 k=m-r,判斷是否匹配前綴串，如果prefix[k]=true,滑動r位。

• 如果兩條規則都沒有找到可以匹配好后綴及其后綴子串的子串，我們就將整個模式串后移 m 位。

平均的情況時間復雜度O(n/m)，空間復雜度bc[], prefix[],suffix[]  O(m+bc.length)

因為好后綴和壞字符規則是獨立的，如果我們運行的環境對內存要求苛刻，可以只使用好后綴規則，不使用壞字符規則，這樣就可以避免 bc 數組過多的內存消耗。不過，單純使用好后綴規則的 BM 算法效率就會下降一些了。

實際上，我前面講的 BM 算法是個初級版本。為了讓你能更容易理解，有些復雜的優化我沒有講。基于我目前講的這個版本，在極端情況下，預處理計算 suffix 數組、prefix 數組的性能會比較差。比如模式串是 aaaaaaa 這種包含很多重復的字符的模式串，預處理的時間復雜度就是 O(m^2)。當然，大部分情況下，時間復雜度不會這么差。關于如何優化這種極端情況下的時間復雜度退化，如果感興趣，你可以自己研究一下。

實際上，BM 算法的時間復雜度分析起來是非常復雜，這篇論文“A new proof of the linearity of the Boyer-Moore string searching algorithm”證明了在最壞情況下，BM 算法的比較次數上限是 5n。這篇論文“Tight bounds on the complexity of the Boyer-Moore string matching algorithm”證明了在最壞情況下，BM 算法的比較次數上限是 3n。你可以自己閱讀看看。

KMP 算法基本原理

KMP 算法是根據三位作者（D.E.Knuth，J.H.Morris 和 V.R.Pratt）的名字來命名的，算法的全稱是 Knuth Morris Pratt 算法，簡稱為 KMP 算法。

在模式串和主串匹配的過程中，把不能匹配的那個字符仍然叫作壞字符，把已經匹配的那段字符串叫作好前綴。從前往后匹配

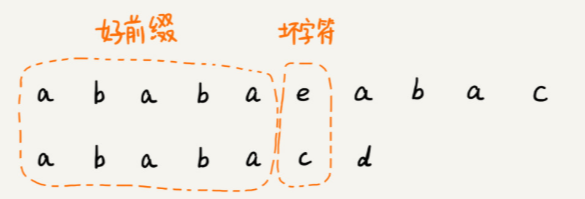
KMP 算法就是在試圖尋找一種規律：在模式串和主串匹配的過程中，當遇到壞字符后，對于已經比對過的好前綴，能否找到一種規律，將模式串一次性滑動很多位？

思路：遇到壞字符，找好前綴的最長匹配前綴子串(好前綴的后綴子串與好前綴的前綴子串匹配)最后下標加1等于j，開始j與i 匹配。如果沒有最長匹配前綴子串，j = 0, j 和i 繼續比較， i 繼續++。

查找好前綴的后綴子串中，最長匹配的那個好前綴的前綴子串{v},長度是 k .我們把模式串一次性往后滑動 j-k 位，相當于，每次遇到壞字符的時候，我們就把 j 更新為 k，i 不變，然后繼續比較。

為了表述起來方便，我把好前綴的所有后綴子串中，最長的可匹配前綴子串的那個后綴子串，叫作最長可匹配后綴子串；對應的前綴子串，叫作最長可匹配前綴子串

最長可匹配后綴子串和最長可匹配前綴子串是相同的，只是位置不一樣，如下圖

如何求好前綴的最長可匹配前綴最后字符下標呢？

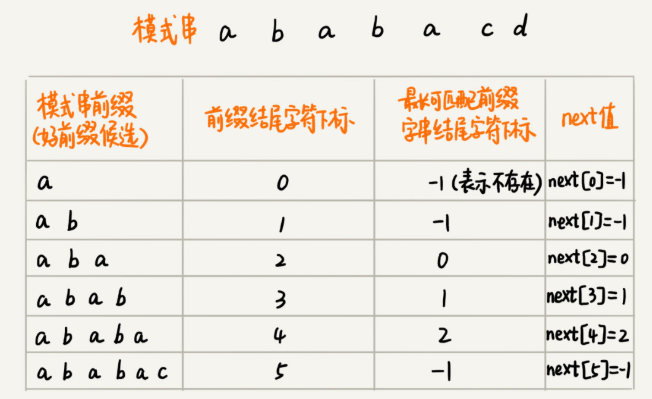
找到模式串的所有好前綴，與自身比較（求最長可匹配前綴,[前綴后綴相匹配]），求得next數組，數組的下標是每個好前綴結尾字符下標，數組的值是這個好前綴的最長可以匹配前綴子串的結尾字符下標。兩個下標

next算法思路：

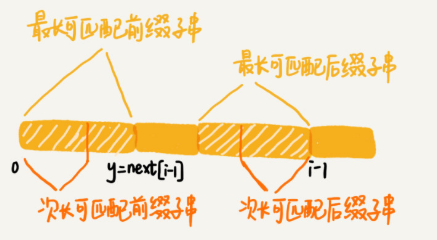
可以利用next[i-1] 求next[i].

考察完所有的 b[0, i-1] 的可匹配后綴子串 b[y, i-1], 如果它對應的前綴子串的下一個字符等于 b[i]，那這個 b[y, i] 就是 b[0, i] 的最長可匹配后綴子串。

以ababacd為例，char數組為arr，當i=5， arr[i] =  'c'  , 此時k = 2  ,  arr[k+1]!=arr[i]  不匹配， 找arr[0,i-1] 中次長可匹配子串最后下標位置。可以通過在arr[0,i-1]中0到最長可以匹配前綴子串的結尾字符下標next[k]找, 找最長可匹配前綴下標，再判斷。

// b 表示模式串，m 表示模式串的長度  ababacd  

private  int[] getNexts(char[] b, int m) {  

    int[] next = new int[m];  

    next[0] = -1; // 好前綴為一個字符，省去操作，記為-1  

    int k = -1;  

    for (int i = 1; i < m; ++i) {  

        while (k != -1 && b[k + 1] != b[i]) {  

            k = next[k]; // 巧妙  

        }  

        // 好前綴, 前綴字符和后綴字符   

        // aa next[1]=0    

        // aba next[2] = 0  | abab next[3] = 1 | ababa next[4]=2  

        if (b[k + 1] == b[i]) {  

            ++k;  

        }  

        // i 為好前綴結尾下標字符  

        // next[i] 表示最長可以匹配前綴子串的結尾字符下標  

        next[i] = k;  

    }  

    return next;  

}  

{  上面理解了，這里就不必看了

利用已經計算出來的 next 值，我們是否可以快速推導出 next[i] 的值呢？

如果 next[i-1]=k-1（最長可匹配前綴子串最后下標），也就是說，子串 b[0, k-1] 是 b[0, i-1] 的最長可匹配前綴子串。如果子串 b[0, k-1] 的下一個字符 b[k]，與 b[0, i-1] 的下一個字符 b[i] 匹配，那子串 b[0, k] 就是 b[0, i] 的最長可匹配前綴子串。

如果 b[0, k-1] 的下一字符 b[k] 跟 b[0, i-1] 的下一個字符 b[i] 不相等呢？這個時候就不能簡單地通過 next[i-1] 得到 next[i] 了。這個時候該怎么辦呢？

我們假設 b[0, i] 的最長可匹配后綴子串是 b[r, i]。如果我們把最后一個字符去掉，那 b[r, i-1] 肯定是 b[0, i-1] 的可匹配后綴子串，但不一定是最長可匹配后綴子串，如abaabab。

既然 b[0, i-1] 最長可匹配后綴子串對應的前綴子串的下一個字符并不等于 b[i]，那么我們就可以考察 b[0, i-1] 的次長可匹配后綴子串 b[x, i-1] 對應的可匹配前綴子串 b[0, i-1-x] 的下一個字符 b[i-x] 是否等于 b[i]。如果等于，那 b[x, i] 就是 b[0, i] 的最長可匹配后綴子串。

}

KMP 算法只需要一個額外的 next 數組，數組的大小跟模式串相同。所以空間復雜度是 O(m)，m 表示模式串的長度。next 數組計算的時間復雜度是 O(m)。

所以，綜合兩部分的時間復雜度，KMP 算法的時間復雜度就是 O(m+n)。

多模式串匹配算法：也就是在一個串中同時查找多個串

利用：trie 樹 

ac自動機

AC 自動機算法，全稱是 Aho-Corasick 算法。AC 自動機實際上就是在 Trie 樹之上，加了類似 KMP 的 next 數組，只不過此處的 next 數組是構建在樹上罷了。

AC 自動機的構建，包含兩個操作：

• 將多個模式串構建成 Trie 樹；

• 在 Trie 樹上構建失敗指針（相當于 KMP 中的失效函數 next 數組）。要構建每個節點的失敗指針，需要一個隊列。

Trie 樹中的每一個節點都有一個失敗指針。p 的失敗指針就是從 root 走到紫色節點形成的字符串 abc，跟所有模式串前綴匹配的最長可匹配后綴子串，就是箭頭指的 bc 模式串。

字符串 abc 的后綴子串有兩個 bc，c，我們拿它們與其他模式串匹配，如果某個后綴子串可以匹配某個模式串的前綴，那我們就把這個后綴子串叫作可匹配后綴子串。

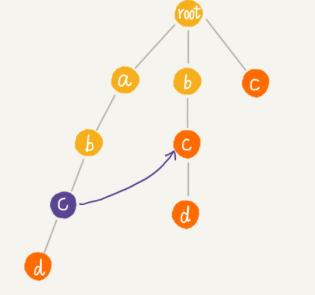 后綴子串（bc,c ）跟模式串的前綴匹配

規律：如果我們把樹中相同深度的節點放到同一層，那么某個節點的失敗指針只有可能出現在它所在層的上一層。

我們可以像 KMP 算法那樣，當我們要求某個節點的失敗指針的時候，我們通過已經求得的、深度更小的那些節點的失敗指針來推導。也就是說，我們可以逐層依次來求解每個節點的失敗指針。所以，失敗指針的構建過程，是一個按層遍歷樹的過程。

首先 root 的失敗指針為 NULL，也就是指向自己。當我們已經求得某個節點 p 的失敗指針之后，如何尋找它的子節點的失敗指針呢？

我們假設節點 p 的失敗指針指向節點 q，我們看節點 p 的子節點 pc 對應的字符，是否也可以在節點 q 的子節點中找到。如果找到了節點 q 的一個子節點 qc，對應的字符跟節點 pc 對應的字符相同，則將節點 pc 的失敗指針指向節點 qc。

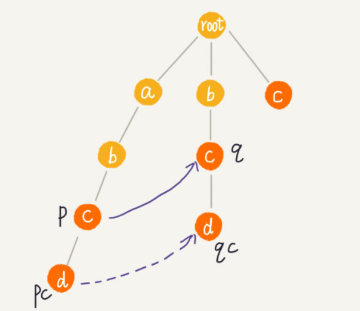
如果節點 q 中沒有子節點的字符等于節點 pc 包含的字符，則令 q=q->fail（fail 表示失敗指針，這里有沒有很像 KMP 算法里求 next 的過程？），繼續上面的查找，直到 q 是 root 為止，如果還沒有找到相同字符的子節點，就讓節點 pc 的失敗指針指向 root。

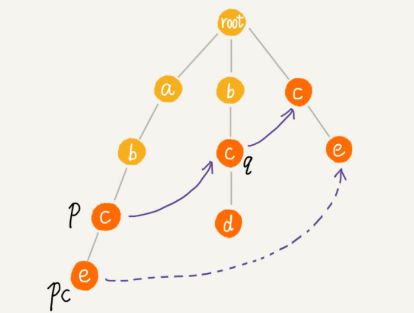
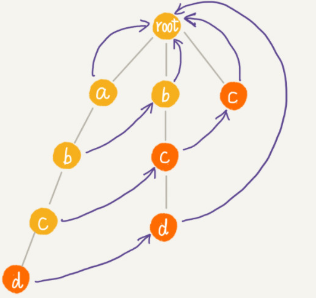
如何在 AC 自動機上匹配主串？

主串遍歷，在root每一個分支匹配，當某個分支匹配了一部分如a->b->c，下一個d沒匹配到，就用失敗指針c = c ->fail  (失敗指針指向的位置，前面都是匹配的。)，再接著匹配。

AC 自動機實現的敏感詞過濾系統，是否比單模式串匹配方法更高效呢？

首先，我們需要將敏感詞構建成 AC 自動機，包括構建 Trie 樹以及構建失敗指針。Trie 樹構建的時間復雜度是 O(m*len)，其中 len 表示敏感詞的平均長度，m 表示敏感詞的個數。那構建失敗指針的時間復雜度是多少呢？

假設 Trie 樹中總的節點個數是 k，每個節點構建失敗指針的時候，（你可以看下代碼）最耗時的環節是 while 循環中的 q=q->fail，每運行一次這個語句，q 指向節點的深度都會減少 1，而樹的高度最高也不會超過 len，所以每個節點構建失敗指針的時間復雜度是 O(len)。整個失敗指針的構建過程就是 O(k*len)。

用 AC 自動機做匹配的時間復雜度是多少？

跟剛剛構建失敗指針的分析類似，for 循環依次遍歷主串中的每個字符，for 循環內部最耗時的部分也是 while 循環，而這一部分的時間復雜度也是 O(len)，所以總的匹配的時間復雜度就是 O(n*len)。因為敏感詞并不會很長，而且這個時間復雜度只是一個非常寬泛的上限，實際情況下，可能近似于 O(n)，所以 AC 自動機做敏感詞過濾，性能非常高。

以上就是“c++字符串匹配的知識點有哪些”這篇文章的所有內容，感謝各位的閱讀！相信大家閱讀完這篇文章都有很大的收獲，小編每天都會為大家更新不同的知識，如果還想學習更多的知識，請關注億速云行業資訊頻道。