二叉樹的非遞歸實現

  之前一直覺得二叉樹使用遞歸來實現就感覺有點繞，今天才發現二叉樹使用非遞歸來實現更加的繞，但是考慮到我們得使用非遞歸來提高二叉樹的遍歷效率，使用非遞歸是一種比較好的方法。

  三種遞歸遍歷對遍歷的描述，思路非常簡潔，最重要的是三種方法完全統一，大大減輕了我們理解的負擔。現在非遞歸使用棧來實現，利用了棧的先進后出的特點，可以解決。

  二叉樹的遞歸實現之前已經實現過了，我們直接實現非遞歸。并且都使用棧實現

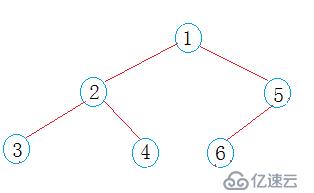
（一）前序遍歷

  對于前序遍歷，我們要解決的問題是何時壓入左右子樹？先壓左子樹還是右子樹？

  答案是顯而易見的，因為是前序遍歷，所以在壓棧根節點，出棧后再壓入左右子樹。并且是先壓右子樹。然后出棧左子樹，最后出棧右子樹。直到棧為空。

void PrevOrder_Nrec()//前序非遞歸實現
	{
		stack<Node*> s;
		if (_root)
			s.push(_root);
		while (!s.empty())
		{
			Node* top = s.top();
			cout << top->_data << " ";
			s.pop();
			if (top->_right)
			{
				s.push(top->_right);
			}
			if (top->_left)
			{
				s.push(top->_left);
			}
		}
	}

（二）中序遍歷

   中序遍歷是一直壓棧，把最左節點都壓入棧內，出棧最左子樹的左節點，然后出棧根節點，然后才出棧右節點。當棧為空時結束。

void MideOrder_Nrec()//中序遍歷非遞歸實現
	{
		stack<Node*> s;
		Node* cur = _root;
		while (!s.empty()||cur)
		{
			while (cur)
			{
				s.push(cur);
				cur = cur->_left;
			}
			if (!s.empty())
			{
				Node* tmp = s.top();
				s.pop();
				cout << tmp->_data << " ";
				cur = tmp->_right;
			}
		}
	}

（三）后序遍歷

  后序遍歷比較難辦，因為我們要找到一棵樹，首先遍歷到的都是樹的根節點，在后序遍歷中，得先把左右子樹都遍歷以后才能輸出根節點。左子樹比較好辦，我們可以把左節點看作是一顆子樹的根節點，所以我們必須要創建一個指針來標識是否我們已經訪問過右子樹。我們把這個指針名為prev，表示上一個訪問的節點，讓他與根節點的右節點比如果相等說明已經訪問過了，可以出棧根。否則訪問右節點。

void RearOrder_Nrec()//后序遍歷非遞歸實現
	{
		stack<Node*> s;
		Node* cur = _root;
		Node* prev = NULL;
		while (cur || !s.empty())
		{
			while (cur)
			{
				s.push(cur);
				cur = cur->_left;
			}
			if (!s.empty())
			{
				Node* top = s.top();
				if (top->_right == prev)//判斷是否已經訪問了根節點的右子樹
				{
					s.pop();
					cout << top->_data << " ";
					prev = top;
				}
				else
				{
					cur = top->_right;//如果沒有就去訪問右子樹
					prev = top->_right;
				}
			}
		}
	}

 如果一棵樹深度很大，那么非遞歸比遞歸的效率高很多，但是遞歸比非遞歸好理解，怎樣取舍看情況吧。