您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
堆排序(Heapsort)是指利用堆這種數據結構所設計的一種排序算法。堆積是一個近似完全二叉樹的結構,并同時滿足堆積的性質:即子結點的鍵值或索引總是小于(或者大于)它的父節點。
堆排序的平均時間復雜度為Ο(nlogn) 。
算法步驟:
1. 創建一個堆H[0..n-1]
2. 把堆首(最大值)和堆尾互換
3. 把堆的尺寸縮小1,并調用shift_down(0),目的是把新的數組頂端數據調整到相應位置
4. 重復步驟2,直到堆的尺寸為1
堆:
堆實際上是一棵完全二叉樹,其任何一非葉節點滿足性質: Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2] 即任何一非葉節點的關鍵字不大于或者不小于其左右孩子節點的關鍵字。 堆分為大頂堆和小頂堆,滿足Key[i]>=Key[2i+1]&&key>=key[2i+2]稱為大頂堆,滿足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]稱為小頂堆。由上述性質可知大頂堆的堆頂的關鍵字肯定是所有關鍵字中最大的,小頂堆的堆頂的關鍵字是所有關鍵字中最小的。
堆排序思想:
利用大頂堆(小頂堆)堆頂記錄的是最大關鍵字(最小關鍵字)這一特性,使得每次從無序中選擇最大記錄(最小記錄)變得簡單。 其基本思想為(大頂堆): 1)將初始待排序關鍵字序列(R1,R2….Rn)構建成大頂堆,此堆為初始的無序區; 2)將堆頂元素R[1]與最后一個元素R[n]交換,此時得到新的無序區(R1,R2,……Rn-1)和新的有序區(Rn),且滿足R[1,2...n-1]<=R[n]; 3)由于交換后新的堆頂R[1]可能違反堆的性質,因此需要對當前無序區(R1,R2,……Rn-1)調整為新堆,然后再次將R[1]與無序區最后一個元素交換,得到新的無序區(R1,R2….Rn-2)和新的有序區(Rn-1,Rn)。不斷重復此過程直到有序區的元素個數為n-1,則整個排序過程完成。 操作過程如下: 1)初始化堆:將R[1..n]構造為堆; 2)將當前無序區的堆頂元素R[1]同該區間的最后一個記錄交換,然后將新的無序區調整為新的堆。 因此對于堆排序,最重要的兩個操作就是構造初始堆和調整堆,其實構造初始堆事實上也是調整堆的過程,只不過構造初始堆是對所有的非葉節點都進行調整。
一個圖示實例
給定一個整形數組a[]={16,7,3,20,17,8},對其進行堆排序。 首先根據該數組元素構建一個完全二叉樹,得到
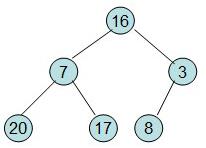
然后需要構造初始堆,則從最后一個非葉節點開始調整,調整過程如下:
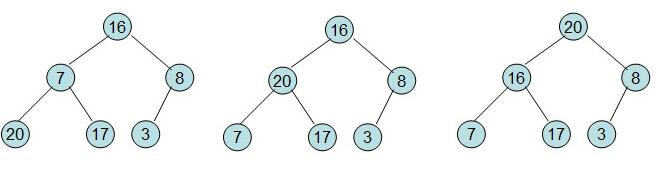
20和16交換后導致16不滿足堆的性質,因此需重新調整

這樣就得到了初始堆。
先進行一次調整時其成為大頂堆,
即每次調整都是從父節點、左孩子節點、右孩子節點三者中選擇最大者跟父節點進行交換(交換之后可能造成被交換的孩子節點不滿足堆的性質,因此每次交換之后要重新對被交換的孩子節點進行調整)。有了初始堆之后就可以進行排序了。
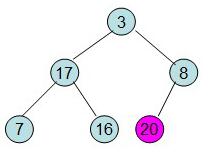
此時3位于堆頂不滿堆的性質,則需調整繼續調整
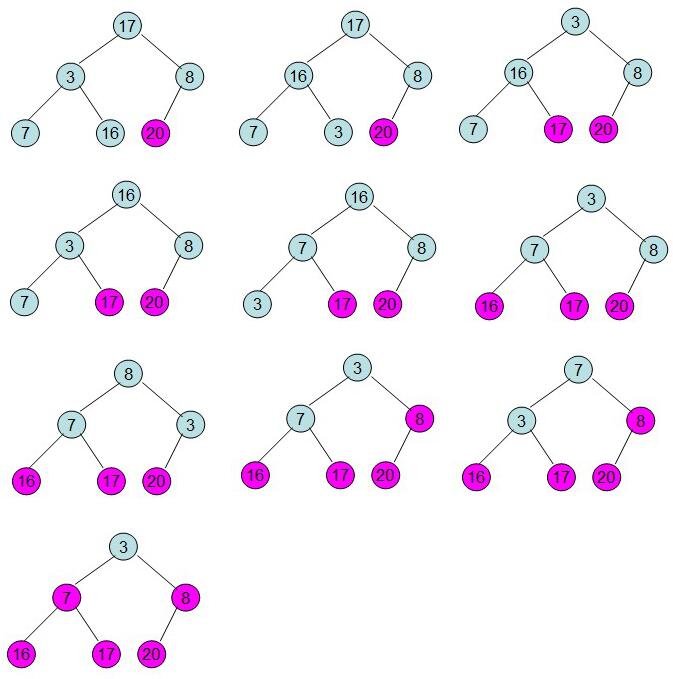
這樣整個區間便已經有序了。從上述過程可知,堆排序其實也是一種選擇排序,是一種樹形選擇排序。只不過直接選擇排序中,為了從R[1...n]中選擇最大記錄,需比較n-1次,然后從R[1...n-2]中選擇最大記錄需比較n-2次。事實上這n-2次比較中有很多已經在前面的n-1次比較中已經做過,而樹形選擇排序恰好利用樹形的特點保存了部分前面的比較結果,因此可以減少比較次數。對于n個關鍵字序列,最壞情況下每個節點需比較log2(n)次,因此其最壞情況下時間復雜度為nlogn。堆排序為不穩定排序,不適合記錄較少的排序。 上面描述了這么多,簡而言之,堆排序的基本做法是:首先,用原始數據構建成一個大(小)堆作為原始無序區,然后,每次取出堆頂元素,放入有序區。由于堆頂元素被取出來了,我們用堆中最后一個元素放入堆頂,如此,堆的性質就被破壞了。我們需要重新對堆進行調整,如此繼續N次,那么無序區的N個元素都被放入有序區了,也就完成了排序過程。
(建堆是自底向上)
實際應用:
實際中我們進行堆排序是為了取得一定條件下的最大值或最小值,例如:需要在100個數中找到10個最大值,因此我們定義一個大小為10的堆,把100中的前十個數據建立成小頂堆(堆頂最小),然后從100個數據中的第11個數據開始與堆頂比較,若堆頂小于當前數據,則把堆頂彈出,把當前數據壓入堆頂,然后把數據從堆頂下移到一定位置即可,
代碼:
public class Test0 {
static int[] arr;//堆數組,有效數組
public Test0(int m){
arr= new int[m];
}
static int m=0;
static int size=0;//用來標記堆中有效的數據
public void addToSmall(int v){
//int[] a = {16,4,5,9,1,10,11,12,13,14,15,2,3,6,7,8,111,222,333,555,66,67,54};
//堆的大小為10
//arr = new int[10];
if(size<arr.length){
arr[size]=v;
add_sort(size);
//add_sort1(size);
size++;
}else{
arr[0]=v;
add_sort1(0);
}
}
public void printSmall(){
for(int i=0;i<size;i++){
System.out.println(arr[i]);
}
}
public void del(){
size--;
arr[0]=arr[9];
add_sort1(0);
}
public void Small(int index){
if(m<arr.length){
add_sort(index);
m++;
}else{
add_sort1(index);
m++;
}
}
public void add_sort( int index){//小頂堆,建堆
/*
* 父節點坐標:index
* 左孩子節點:index*2
* 右孩子節點:index*2+1
*若數組中最后一個為奇數則為 左孩子
*若數組中最后一個為偶數則為 右孩子
若孩子節點比父節點的值大,則進行值交換,若右孩子比左孩子大則進行值交換
*
*/
int par;
if(index!=0){
if(index%2==0){
par=(index-1)/2;
if(arr[index]<arr[par]){
swap(arr,index,par);
add_sort(par);
}
if(arr[index]>arr[par*2]){
swap(arr,index,par*2);
if(arr[index]<arr[par]){
swap(arr,index,par);
}
add_sort(par);
}
}else{
par=index/2;
if(arr[index]<arr[par]){
swap(arr,index,par);
add_sort(par);
}
if(arr[index]<arr[par*2+1]){
swap(arr, index, par*2+1);
if(arr[index]<arr[par]){
swap(arr,index,par);
}
add_sort(par);
}
}
}
}
public void add_sort1(int index){//調整小頂堆
/*調整自頂向下
* 只要孩子節點比父節點的值大,就進行值交換,
*/
int left=index*2;
int right=index*2+1;
int max=0;
if(left<10&&arr[left]<arr[index]){
max=left;
}else{
max=index;
}
if(right<10&&arr[right]<arr[max]){
max=right;
}
if(max!=index){
swap(arr,max,index);
add_sort1(max);
}
}
}
測試代碼:
package 大頂堆;
import java.util.Scanner;
public class Main_test0 {
public static void main(String args[]){
Scanner scan = new Scanner(System.in);
System.out.println("(小頂堆)請輸入堆大小:");
int m=scan.nextInt();
Test0 test = new Test0(m);
int[] a = {16,4,5,9,1,10,11,12,13,14,15,2,3,6,7,8};
for(int i=0;i<a.length;i++){
test.addToSmall(a[i]);
}
test.printSmall();
test.del();
test.printSmall();
scan.close();
}
}
以上這篇Java 堆排序實例(大頂堆、小頂堆)就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。