Python怎么使用numpy產生正態分布隨機數的向量或矩陣操作示例

小編給大家分享一下Python怎么使用numpy產生正態分布隨機數的向量或矩陣操作示例，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

具體如下：

簡單來說，正態分布（Normal distribution）又名高斯分布（Gaussian distribution），是一個在數學、物理及工程等領域都非常重要的概率分布，在統計學的許多方面有著重大的影響力。一般的正態分布可以通過標準正態分布配合數學期望向量和協方差矩陣得到。如下代碼，可以得到滿足一維和二維正態分布的樣本。

示例1（一維正態分布）：

# coding=utf-8
'''
作者：采石工
來源：知乎
'''
import numpy as np
from numpy.linalg import cholesky
import matplotlib.pyplot as plt
sampleNo = 1000;
# 一維正態分布
# 下面三種方式是等效的
mu = 3
sigma = 0.1
np.random.seed(0)
s = np.random.normal(mu, sigma, sampleNo )
plt.subplot(141)
plt.hist(s, 30, normed=True)
np.random.seed(0)
s = sigma * np.random.randn(sampleNo ) + mu
plt.subplot(142)
plt.hist(s, 30, normed=True)
np.random.seed(0)
s = sigma * np.random.standard_normal(sampleNo ) + mu
plt.subplot(143)
plt.hist(s, 30, normed=True)
# 二維正態分布
mu = np.array([[1, 5]])
Sigma = np.array([[1, 0.5], [1.5, 3]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(sampleNo, 2), R) + mu
plt.subplot(144)
# 注意繪制的是散點圖，而不是直方圖
plt.plot(s[:,0],s[:,1],'+')
plt.show()

運行結果：

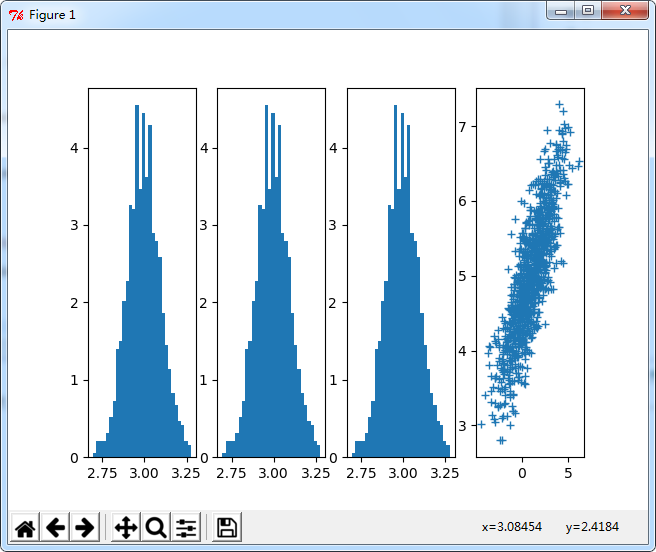
示例2（正態分布）：

#-*- coding:utf-8 -*-
# Python實現正態分布
# 繪制正態分布概率密度函數
import numpy as np
import matplotlib.pyplot as plt
import math
u = 0  # 均值μ
u01 = -2
sig = math.sqrt(0.2) # 標準差δ
x = np.linspace(u - 3*sig, u + 3*sig, 50)
y_sig = np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig)
print x
print "="*20
print y_sig
plt.plot(x, y_sig, "r-", linewidth=2)
plt.grid(True)
plt.show()

運行結果：

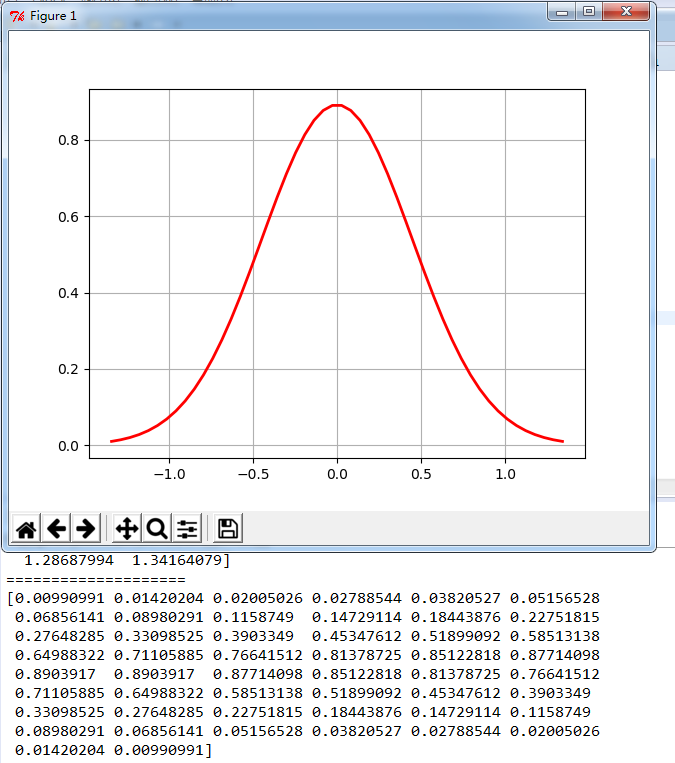
以上是“Python怎么使用numpy產生正態分布隨機數的向量或矩陣操作示例”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！