怎么使用python實現dijkstra最短路由算法的案例

這篇文章主要介紹怎么使用python實現dijkstra最短路由算法的案例，文中介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們一定要看完！

Dijkstra算法:又稱迪杰斯特拉算法，迪杰斯特拉算法是由荷蘭計算機科學家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是從一個頂點到其余各頂點的最短路徑算法，解決的是有向圖中最短路徑問題。迪杰斯特拉算法主要特點是以起始點為中心向外層層擴展，直到擴展到終點為止百度百科。

注意：Dijkstra算法不能處理包含負邊的圖

# dijkstra算法實現，有向圖和路由的源點作為函數的輸入，最短路徑最為輸出
def dijkstra(graph,src):
 # 判斷圖是否為空，如果為空直接退出
 if graph is None:
 return None
 nodes = [i for i in range(len(graph))] # 獲取圖中所有節點
 visited=[] # 表示已經路由到最短路徑的節點集合
 if src in nodes:
 visited.append(src)
 nodes.remove(src)
 else:
 return None
 distance={src:0} # 記錄源節點到各個節點的距離
 for i in nodes:
 distance[i]=graph[src][i] # 初始化
 # print(distance)
 path={src:{src:[]}} # 記錄源節點到每個節點的路徑
 k=pre=src
 while nodes:
 mid_distance=float('inf')
 for v in visited:
  for d in nodes:
  new_distance = graph[src][v]+graph[v][d]
  if new_distance < mid_distance:
   mid_distance=new_distance
   graph[src][d]=new_distance # 進行距離更新
   k=d
   pre=v
 distance[k]=mid_distance # 最短路徑
 path[src][k]=[i for i in path[src][pre]]
 path[src][k].append(k)
 # 更新兩個節點集合
 visited.append(k)
 nodes.remove(k)
 print(visited,nodes) # 輸出節點的添加過程
 return distance,path
if __name__ == '__main__':
 graph_list = [ [0, 2, 1, 4, 5, 1],
  [1, 0, 4, 2, 3, 4],
  [2, 1, 0, 1, 2, 4],
  [3, 5, 2, 0, 3, 3],
  [2, 4, 3, 4, 0, 1],
  [3, 4, 7, 3, 1, 0]]

 distance,path= dijkstra(graph_list, 0) # 查找從源點0開始帶其他節點的最短路徑
 print(distance,path)

節點的遍歷過程如下：

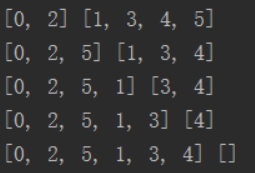
最短路徑輸出：

以上是“怎么使用python實現dijkstra最短路由算法的案例”這篇文章的所有內容，感謝各位的閱讀！希望分享的內容對大家有幫助，更多相關知識，歡迎關注億速云行業資訊頻道！