溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
Dijkstra算法
迪杰斯特拉算法是由荷蘭計算機科學家狄克斯特拉于1959 年提出的,因此又叫狄克斯特拉算法。是從一個頂點到其余各頂點的最短路徑算法,解決的是有向圖中最短路徑問題。迪杰斯特拉算法主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。
迪杰斯特拉算法是求從某一個起點到其余所有結點的最短路徑,是一對多的映射關系,是一種貪婪算法
示例:
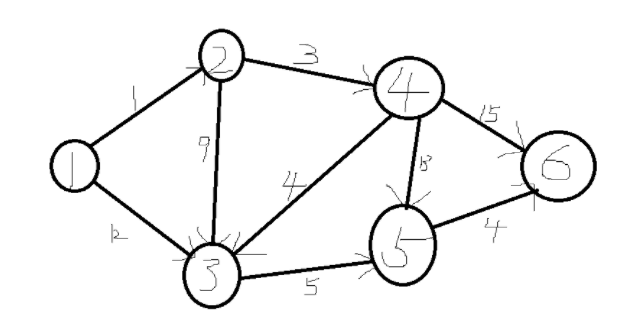
算法
算法實現流程思路:
迪杰斯特拉算法每次只找離起點最近的一個結點,并將之并入已經訪問過結點的集合(以防重復訪問,陷入死循環),然后將剛找到的最短路徑的結點作為中間結點來更新相鄰結點的路徑長度,這樣循環找到圖中一個個結點的最短路徑。
"""
輸入
graph 輸入的圖
src 原點
返回
dis 記錄源點到其他點的最短距離
path 路徑
"""
import json
def dijkstra(graph,src):
if graph ==None:
return None
# 定點集合
nodes = [i for i in range(len(graph))] # 獲取頂點列表,用鄰接矩陣存儲圖
# 頂點是否被訪問
visited = []
visited.append(src)
# 初始化dis
dis = {src:0}# 源點到自身的距離為0
for i in nodes:
dis[i] = graph[src][i]
path={src:{src:[]}} # 記錄源節點到每個節點的路徑
k=pre=src
while nodes:
temp_k = k
mid_distance=float('inf') # 設置中間距離無窮大
for v in visited:
for d in nodes:
if graph[src][v] != float('inf') and graph[v][d] != float('inf'):# 有邊
new_distance = graph[src][v]+graph[v][d]
if new_distance <= mid_distance:
mid_distance=new_distance
graph[src][d]=new_distance # 進行距離更新
k=d
pre=v
if k!=src and temp_k==k:
break
dis[k]=mid_distance # 最短路徑
path[src][k]=[i for i in path[src][pre]]
path[src][k].append(k)
visited.append(k)
nodes.remove(k)
print(nodes)
return dis,path
if __name__ == '__main__':
# 輸入的有向圖,有邊存儲的就是邊的權值,無邊就是float('inf'),頂點到自身就是0
graph = [
[0, float('inf'), 10, float('inf'), 30, 100],
[float('inf'), 0, 5, float('inf'), float('inf'), float('inf')],
[float('inf'), float('inf'), 0, 50, float('inf'), float('inf')],
[float('inf'), float('inf'), float('inf'), 0, float('inf'), 10],
[float('inf'), float('inf'), float('inf'), 20, 0, 60],
[float('inf'), float('inf'), float('inf'), float('inf'), float('inf'), 0]]
dis,path= dijkstra(graph, 0) # 查找從源點0開始帶其他節點的最短路徑
print(dis)
print(json.dumps(path, indent=4))
總結
以上就是這篇文章的全部內容了,希望本文的內容對大家的學習或者工作具有一定的參考學習價值,謝謝大家對億速云的支持。如果你想了解更多相關內容請查看下面相關鏈接
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。