您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
Dijkstra最短路徑算法是什么,相信很多沒有經驗的人對此束手無策,為此本文總結了問題出現的原因和解決方法,通過這篇文章希望你能解決這個問題。
01
—
單源最短路徑
首先解釋什么是單源最短路徑,所謂單源最短路徑就是指定一個出發頂點,計算從該源點出發到其他所有頂點的最短路徑。如下圖所示,如果源點設為A,那么單源最短路徑問題,就是求解從A到B,從A到C,從A到D,從A到E,從A到F的最短路徑。
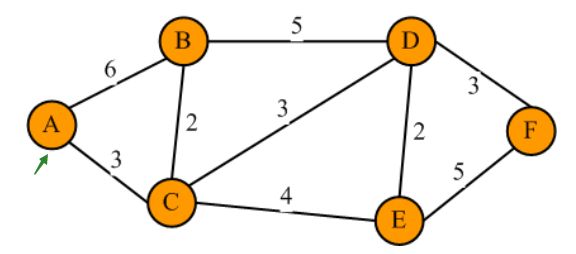
比如,從A到D的最短路徑,通過肉眼觀察可以得出為如下,A->C->D,距離等于3+3=6,其中A->C邊上的數值3稱為權重,又知這是無向圖,從C到A的權重也為3。
02
—
Dijkstra算法求單源最短路徑
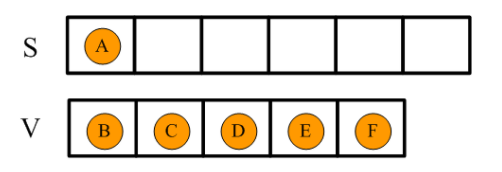
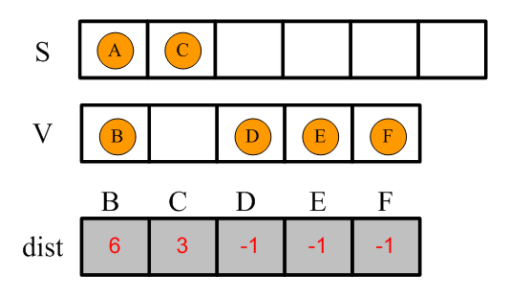
這個算法首先設置了兩個集合,S集合和V集合。S集合初始只有源頂點即頂點A,V集合初始為除了源頂點以外的其他所有頂點,如下圖所示:
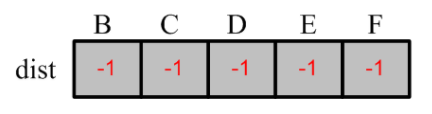
設置一個從A到各頂點的緩存字典,作為算法的輸出,初始時,統一設置為 -1,
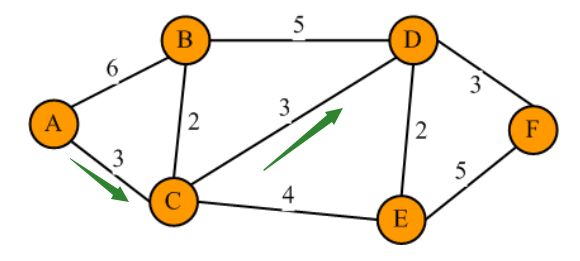
接下來,開始求解A到某個節點的第一個最短距離,通過鄰接矩陣,我們自然可以找到與A存在邊連接的所有頂點,即頂點B,頂點C;
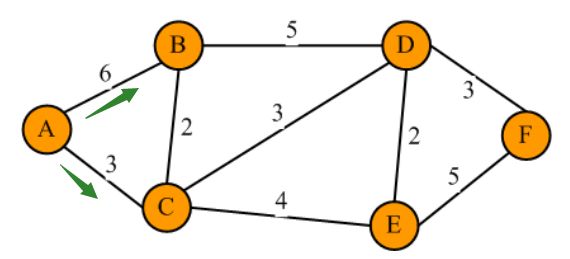
Dijkstra算法會選擇A->B,A->C的距離最小的,挑選C,放入S集合中,但是更新dist字典的時候,可以同時更新A->B和A->C的距離,示意圖如下:
再進一步,找S集合的最后一個元素C在V中與之關聯的所有邊:B,D,E,因此
A->B = 3 + 2 =5
A->D = 3 + 3 = 6
A->E = 3 + 4 = 7
根據Dijkstra算法,選取最小距離,即B進入S集合,并且,Dijkstra算法要和dist字典中A->B 距離做一次比較,
如果dist(A->B)!=-1,且5 <= dist(A->B),則更新dist(A->B)=5;
如果dist(A->B)!=-1,且5 > dist(A->B),則不更新dist(A->B);
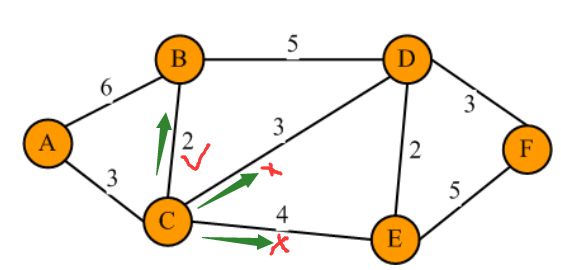
注意,根據這種討論,實際上我們考慮了兩種從A到B的路徑:A->B,A->C->B,但是到達B的路徑不只這兩條,因為經過D也可以到B,如果這些路勁中出現比距離5還小的路徑的話,那么Dijkstra算法是不是有漏洞呢?這個考慮是正確的,但是Dijkstra算法假定了邊的權重值必須大于0,這樣的假定,可以避免經過D到B的路徑不可能小于5,因為除了A->B外,其他所有達到B的路徑必然經過C,與C相連的頂點中,到達B是最小的,所以經過其他邊到達B后,距離不可能小于5。
以上分析就是Dijkstra算法的基本思想,直到集合V的元素個數為0為止,最終的dist字典如下:
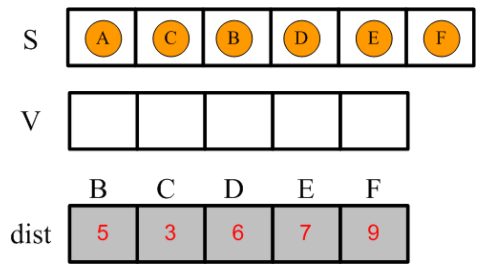
03
—
Dijkstra算法總結
算法的基本思路:
1. 初始化兩個集合,S集合和V集合。S集合初始只有源頂點即頂點A,V集合初始為除了源頂點以外的其他所有頂點,dist字典值都為-1;緊接著,根據鄰接矩陣,找出與A存在邊的頂點list,遍歷list,依次更新dist字典(比如list={B,C},則依次更新字典鍵為B,C 的距離值), 求出與 A 距離最近的頂點,并從V集合中移除到S集合中;
2. 抓出S集合的最后一個元素,根據鄰接矩陣,找出V集合中與之存在邊的頂點list,遍歷list,求出與之距離最小的頂點,并從V集合中移除到S集合中。
3 dist更新,分情況討論,如果遍歷到的頂點不是與之最小的頂點,則直接更新dist字典,比如list={D,E},則依次更新字典鍵為D,E的距離值,如果遍歷到的頂點是與之最小的頂點,則需要判斷dist[此頂點]與當前的距離,如果后者小,才更新dist[此頂點],否則不更新。
4. 重復2和3,直到V集合元素為空為止。
看完上述內容,你們掌握Dijkstra最短路徑算法是什么的方法了嗎?如果還想學到更多技能或想了解更多相關內容,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。