您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編給大家分享一下Tensorflow如何實現XOR運算的方式,相信大部分人都還不怎么了解,因此分享這篇文章給大家參考一下,希望大家閱讀完這篇文章后大有收獲,下面讓我們一起去了解一下吧!
對于“XOR”大家應該都不陌生,我們在各種課程中都會遇到,它是一個數學邏輯運算符號,在計算機中表示為“XOR”,在數學中表示為“ ”,學名為“異或”,其來源細節就不詳細表明了,說白了就是兩個a、b兩個值做異或運算,若a=b則結果為0,反之為1,即“相同為0,不同為1”.
”,學名為“異或”,其來源細節就不詳細表明了,說白了就是兩個a、b兩個值做異或運算,若a=b則結果為0,反之為1,即“相同為0,不同為1”.
在計算機早期發展中,邏輯運算廣泛應用于電子管中,這一點如果大家學習過微機原理應該會比較熟悉,那么在神經網絡中如何實現它呢,早先我們使用的是感知機,可理解為單層神經網絡,只有輸入層和輸出層(在吳恩達老師的系列教程中曾提到過這一點,關于神經網絡的層數,至今仍有異議,就是說神經網絡的層數到底包不包括輸入層,現今多數認定是不包括的,我們常說的N層神經網絡指的是隱藏層+輸出層),但是感知機是無法實現XOR運算的,簡單來說就是XOR是線性不可分的,由于感知機是有輸入輸出層,無法線性劃分XOR區域,于是后來就有了使用多層神經網絡來解決這一問題的想法~~
關于多層神經網絡實現XOR運算可大致這么理解:
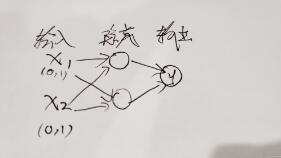
兩個輸入均有兩個取值0和1,那么組合起來就有四種可能,即[0,0]、[0,1]、[1,0]、[1,1],這樣就可以通過中間的隱藏層進行異或運算了~
咱們直接步入正題吧,對于此次試驗我們只需要一個隱藏層即可,關于神經網絡 的基礎知識建議大家去看一下吳恩達大佬的課程,真的很棒,百看不厭,真正的大佬是在認定學生是絕對小白的前提下去講解的,所以一般人都能聽懂~~接下來的圖純手工操作,可能不是那么準確,但中心思想是沒有問題的,我們開始吧:
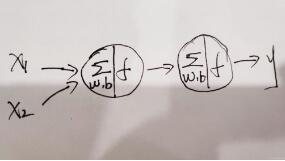
上圖是最基本的神經網絡示意圖,有兩個輸入x1、x2,一個隱藏層,只有一個神經元,然后有個輸出層,這就是最典型的“輸入層+隱藏層+輸出層”的架構,對于本題目,我們的輸入和輸出以及整體架構如下圖所示:
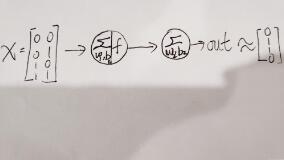
輸入量為一個矩陣,0和0異或結果為0,0和1異或結果為1,依次類推,對應我們的目標值為[0,1,1,0],最后之所以用約等號是因為我們的預測值與目標值之間會有一定的偏差,如果訓練的好那么這二者之間是無限接近的。
我們直接上全部代碼吧,就不分步進行了,以為這個實驗本身難度較低,且代碼注釋很清楚,每一步都很明確,如果大家有什么不理解的可以留言給我,看到必回:
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import numpy as np
import tensorflow as tf
#定義輸入值與目標值
X=np.array([[0,0],[0,1],[1,0],[1,1]])
Y=np.array([[0],[1],[1],[0]])
#定義占位符,從輸入或目標中按行取數據
x=tf.placeholder(tf.float32,[None,2])
y=tf.placeholder(tf.float32,[None,1])
#初始化權重,使其滿足正態分布,w1和w2分別為輸入層到隱藏層和隱藏層到輸出層的權重矩陣
w1=tf.Variable(tf.random_normal([2,2]))
w2=tf.Variable(tf.random_normal([2,1]))
#定義b1和b2,分別為隱藏層和輸出層的偏移量
b1=tf.Variable([0.1,0.1])
b2=tf.Variable([0.1])
#使用Relu激活函數得到隱藏層的輸出值
a=tf.nn.relu(tf.matmul(x,w1)+b1)
#輸出層不用激活函數,直接獲得其值
out=tf.matmul(a,w2)+b2
#定義損失函數MSE
loss=tf.reduce_mean(tf.square(out-y))
#優化器選擇Adam
train=tf.train.AdamOptimizer(0.01).minimize(loss)
#開始訓練,迭代1001次(方便后邊的整數步數顯示)
with tf.Session() as session:
session.run(tf.global_variables_initializer()) #初始化變量
for i in range(1001):
session.run(train,feed_dict={x:X,y:Y}) #訓練模型
loss_final=session.run(loss,feed_dict={x:X,y:Y}) #獲取損失
if i%100==0:
print("step:%d loss:%2f" % (i,loss_final))
print("X: %r" % X)
print("pred_out: %r" % session.run(out,feed_dict={x:X}))對照第三張圖片理解代碼更加直觀,我們的隱藏層神經元功能就是將輸入值和相應權重做矩陣乘法,然后加上偏移量,最后使用激活函數進行非線性轉換;而輸出層沒有用到激活函數,因為本次我們不是進行分類或者其他操作,一般情況下隱藏層使用激活函數Relu,輸出層若是分類則用sigmode,當然你也可以不用,本次實驗只是單純地做異或運算,那輸出層就不勞駕激活函數了~
對于標準神經元內部的操作可理解為下圖:
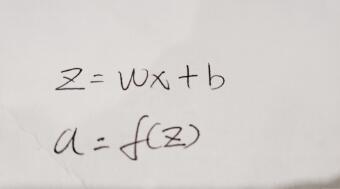
這里的x和w一般寫成矩陣形式,因為大多數都是多個輸入,而矩陣的乘積要滿足一定的條件,這一點屬于線代中最基礎的部分,大家可以稍微了解一下,這里對設定權重的形狀還是很重要的;
看下效果吧:
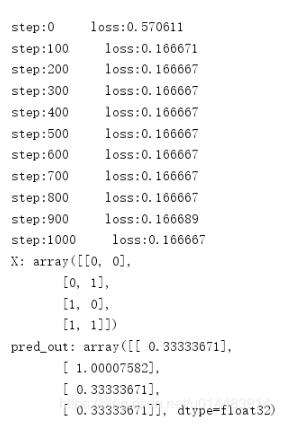
這是我們在學習率為0.1,迭代1001次的條件下得到的結果
然后我們學習率不變,迭代2001次,看效果:
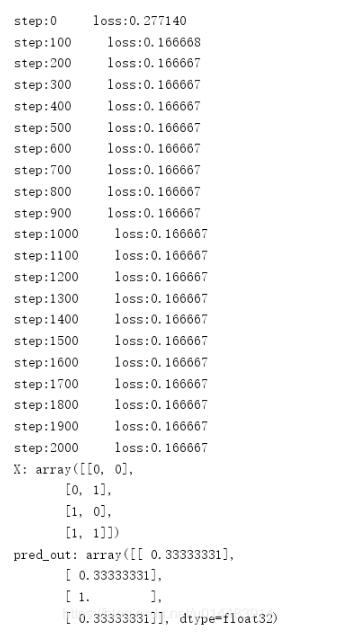
沒有改進,這就說明不是迭代次數的問題,我們還是保持2001的迭代數,將學習率改為0.01,看效果:

以上是“Tensorflow如何實現XOR運算的方式”這篇文章的所有內容,感謝各位的閱讀!相信大家都有了一定的了解,希望分享的內容對大家有所幫助,如果還想學習更多知識,歡迎關注億速云行業資訊頻道!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。