算法時間復雜度及效率（二）

????????今天我們來看下算法復雜度和效率的問題，在判斷一個算法的效率時，操作數量中的常數項和其他次要項常常是可以忽略的，只需要關注最高階項就能得出結論。那么我們如何用符號定性的判斷算法的效率呢？算法的復雜度分為兩部分：1、時間復雜度，即算法運行后對時間需求量的定性描述；2、空間復雜度，即算法運行后對空間需求量的定性描述。

????????數據結構重點關注的是算法的效率問題，因此，我們后面會集中于討論算法的時間復雜度；但其使用的方法完全可以用于空間復雜度的判斷！我們經常在進行算法的時間復雜度用大O表示法來進行分析。下來對此種方法進行說明，算法效率嚴重依賴于操作（Operation）數量；操作數量的估算可以作為時間復雜度的估算；在判斷時首先關注操作數量的最高次項。如下：

????????下來我們來分析下常見的時間復雜度：

????????1、線性階時間復雜度：O(n)。如下：

????????2、對數階時間復雜度：O(logn)。如下

????????3、平方階時間復雜度：O(n2)。如下：

??????? 下來我們來看看常見的時間復雜度，如下圖所示

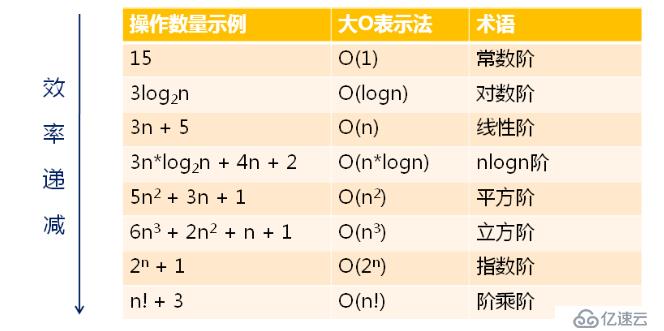
????????常見的時間復雜度的比較，如下

????????下面我們通過實例來進行分析下，下面的函數程序復雜度是怎樣的

int?find(int?a[],?int?n,?int?v)
{
????int?ret?=?-1;
????
????for(int?i=0;?i<=n;?i++)
????{
????????if(?a[i]?==?v?)
????????{
????????????ret?=?i;
????????????break;
????????}
????}
????
????return?ret;
}

????????我們如果定義的數組 a[5] = {1, 2, 3, 4, 5}； 如果是 int min = find(a, 5, 1)； 這種則是最好情況了，僅需執行 1 次循環，此時便是 O(1)；如果是 int max = find(a, 5, 5)；此時便是最壞的情況了，需要全部執行，此時便是 O(n)。那么此時算法的最好與最壞情況便體現出來了，當算法在最乖情況下仍然能滿足需求時，可以推斷，算法的最好情況和平均情況都滿足需求。在以后沒有進行特殊說明時，所分析算法的時間復雜度都是指最壞時間復雜度。

????????算法的空間復雜度（Space Complexity），其定義為 S(n) = S(f(n))。其中 n 為算法的問題規模，f(n) 為空間使用函數，與 n 相關。推倒時間復雜度的方法同樣適用于空間復雜度，例如，當算法所需要的空間是常數時，其空間復雜度為 S(1)。我么來看看下面這個程序的空間復雜度為多少

long?sum1(int?n)
{
????long?ret?=?0;
????int*?array?=?new?int[n];
????
????for(int?i=0;?i<n;?i++)
????{
????????array[i]?=?i?+?1;
????}
????
????for(iunt?i=0;?i<n;?i++)
????{
????????ret?+=?array[i];
????}
????
????delete[]?array;
????
????return?ret;
}

????????我們看到第一行為 1，第三行的 ret 定義也為 1，指針數組 array 的定義其空間復雜度為 n，下面兩個進行 for 循環的空間復雜度分別為 1。因此整個程序所需的單位內存為： n + 4；即空間復雜度：S(n+4) = S(n)。那么時間跟空間之間是否存在某種聯系呢？在多數情況下，算法的時間復雜度更令人關注，因為現在的內存都很大。如果有必要的話，可以通過增加額外空間降低時間復雜度；同理，也可以增加算法的耗時降低空間復雜度。下來我們來看個空間換時間的示例代碼，代碼的背景是在 1-1000 中的某些數字搜組成的數組中，設計一個算法類找出出現次數最多的數字。

#include?<iostream>

using?namespace?std;

void?sreach(int?a[],?int?len)
{
????int?pi[1000]?=?{0};
????int?max?=?0;
????
????for(int?i=0;?i<len;?i++)
????{
????????pi[a[i]?-1]++;
????}
????
????for(int?i=0;?i<1000;?i++)
????{
????????if(?max?<?pi[i]?)
????????{
????????????max?=?pi[i];
????????}
????}
????
????for(int?i=0;?i<1000;?i++)
????{
????????if(?max?==?pi[i]?)
????????{
????????????cout?<<?i?+?1?<<?endl;
????????}
????}
}

int?main(int?argc,?char*?argv[])
{
????int?a[]?=?{1,?1,?3,?4,?5,?6,?6,?6,?3,?3};
????
????sreach(a,?sizeof(a)/sizeof(*a));
????
????return?0;
}

????????我們來看看打印結果

????????我們看到打印了 3 和 6，因為最大數 6 和 3 都出現了 3 次。那么此次我們的程序實現中函數的時間復雜度為 O(n)。那么問題來了，當兩個算法的大 O 表示法相同時，是否意味著兩個算法的效率完全相同呢？肯定是不相同的！通過今天對算法的時間復雜度和效率的學習，總結如下：1、時間復雜度是算法運行時對于時間的需求量；2、大 O 表示法用于描述算法的時間復雜度，它只關注操作數量的最高次項；3、常見的時間復雜度為：線性階，平方階和對數階；4、一般而言，在工程中使用的算法其復雜度都不超過 O(n3)；5、算法分析與設計時，重點考慮最壞情況下的時間復雜度，大 O 表示法用于適用于算法的空間復雜度；6、空間換時間是工程開發中常用的策略。