Python算法中時間復雜度問題的示例分析

這篇文章主要介紹了Python算法中時間復雜度問題的示例分析，具有一定借鑒價值，感興趣的朋友可以參考下，希望大家閱讀完這篇文章之后大有收獲，下面讓小編帶著大家一起了解一下。

在實現算法的時候，通常會從兩方面考慮算法的復雜度，即時間復雜度和空間復雜度。顧名思義，時間復雜度用于度量算法的計算工作量，空間復雜度用于度量算法占用的內存空間。

本文將從時間復雜度的概念出發，結合實際代碼示例分析算法的時間復雜度。

漸進時間復雜度

時間復雜度是算法運算所消耗的時間，因為不同大小的輸入數據，算法處理所要消耗的時間是不同的，因此評估一個算運行時間是比較困難的，所以通常關注的是時間頻度，即算法運行計算操作的次數，記為T(n)，其中n稱為問題的規模。

同樣，因為n是一個變量，n發生變化時，時間頻度T(n) 也在發生變化，我們稱時間復雜度的極限情形稱為算法的漸近時間復雜度，記為O(n)，不包含函數的低階和首項系數。

我們以如下 例子來解釋一下：

如上例子中，我們根據代碼上執行的平均時間假設，計算 run_time(n) 函數的時間復雜度，如下：

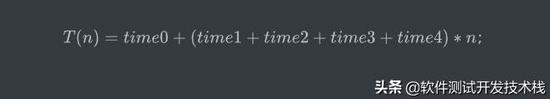
上述時間復雜度計算公式T(n) ，是我們對函數 run_time(n) 進行的時間復雜度的估算。當n 值非常大的時候，T(n)函數中常數項 time0 以及n的系數 (time1+time2+time3+time4) 對n的影響也可以忽略不計了，因此這里函數run_time(n) 的時間復雜度我們可以表示為 O(n)。

因為我們計算的是極限狀態下(如，n非常大)的時間復雜度，因此其中存在以下兩種特性：

低階項相對于高階項產生的影響很小，可以忽略不計。 最高項系數對最高項的影響也很小，可以忽略不計。

根據上述兩種特性，時間復雜度的計算方法：

1.只取最高階項，去掉低階項。

2.去掉最高項的系數。

3.針對常數階，取時間復雜度為O(1)。

我們通過下面例子理解一下常見的時間復雜度，如下：

時間復雜度：常數階 O(1)

時間復雜度：線性階 O(n)

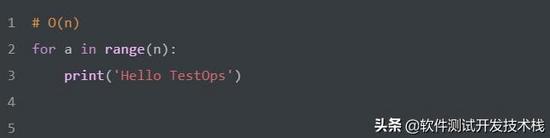
時間復雜度：線性階 O(n)

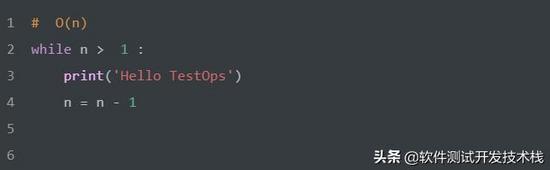
時間復雜度：平方階 O(n^2)

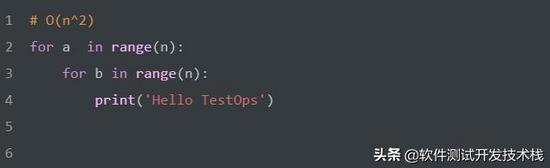
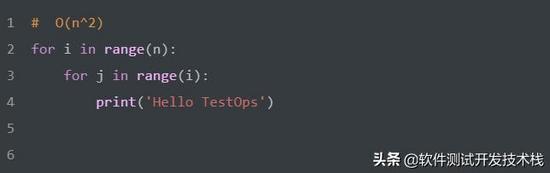
時間復雜度：平方階 O(n^2)

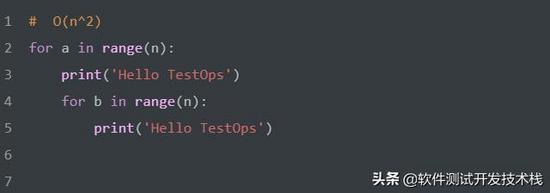
時間復雜度：平方階 O(n^2)

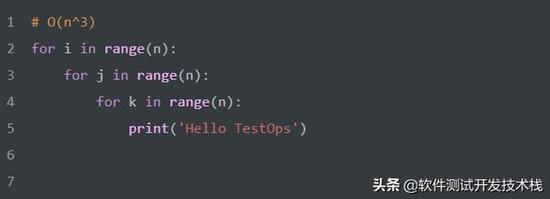
時間復雜度：立方階 O(n^3)

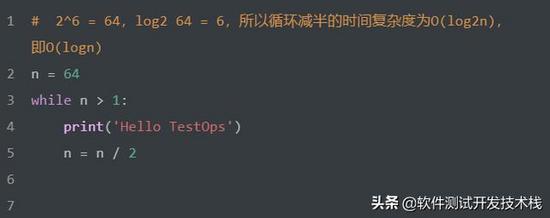
時間復雜度：對數階 O(logn)

隨著問題規模n的不斷增大，上述時間復雜度不斷增大，算法的執行效率越低，時間復雜度排序如下：

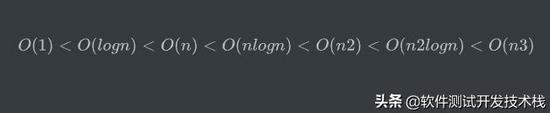
練習一下

如下count_sort 函數實現了計數排序，列表中的數范圍都在0到100之間，列表長度大約為100萬。

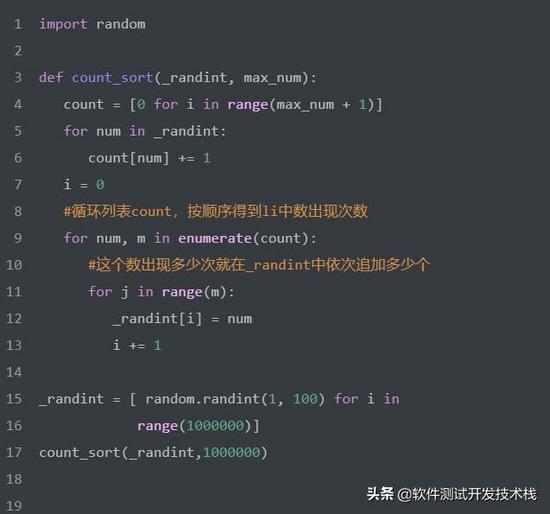
如上count_sort 函數的 空間復雜度為 O(n)，公式如下：

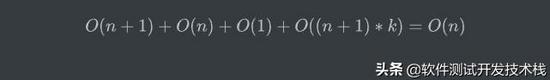
感謝你能夠認真閱讀完這篇文章，希望小編分享的“Python算法中時間復雜度問題的示例分析”這篇文章對大家有幫助，同時也希望大家多多支持億速云，關注億速云行業資訊頻道，更多相關知識等著你來學習!