您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
TreeMap也是Map接口的實現類,它最大的特點是迭代有序,默認是按照key值升序迭代(當然也可以設置成降序)。在前面的文章中講過LinkedHashMap也是迭代有序的,不過是按插入順序或訪問順序,這與TreeMap需要區分開來。TreeMap內部用紅黑樹存儲數據,而不是像HashMap、LinkedHashMap、WeakHashMap一樣使用哈希表來存儲。
此外,TreeMap也是非線程安全的,并且與基于哈希表實現的Map實現類不同,TreeMap的key和value值都不允許為Null。
在介紹紅黑樹之前,先簡單介紹一下排序二叉樹。排序二叉樹是一種特殊結構的二叉樹,可以非常方便地對樹中所有節點進行排序和檢索。
排序二叉樹可以為空樹,如果它不為空,則滿足以下性質:
若它的左子樹不空,則左子樹上所有節點的值均小于它的根節點的值;
若它的右子樹不空,則右子樹上所有節點的值均大于它的根節點的值;
它的左、右子樹也分別為排序二叉樹。
下圖即為一個排序二叉樹:
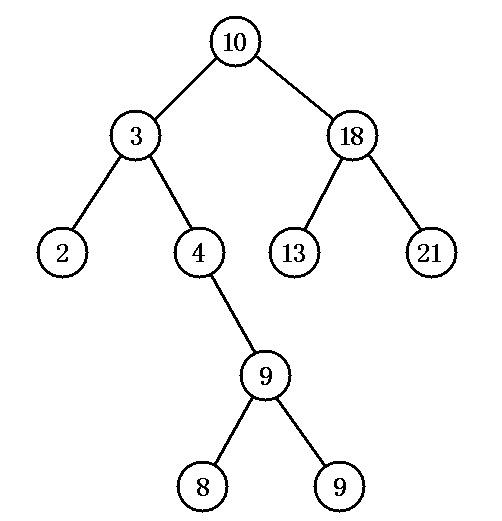
對排序二叉樹,若按中序遍歷就可以得到由小到大的有序序列。
排序二叉樹雖然可以快速檢索,但在最壞的情況下:如果插入的節點集本身就是有序的,要么是由小到大排列,要么是由大到小排列,那么最后得到的排序二叉樹將變成鏈表:所有節點只有左節點(如果插入節點集本身是大到小排列);或所有節點只有右節點(如果插入節點集本身是小到大排列)。在這種情況下,排序二叉樹就變成了普通鏈表,其檢索效率就會很差。
而紅黑樹則是對這一點進行了改進的排序二叉樹,也叫“對稱二叉.B樹”,它在原有的排序二叉樹增加了如下幾個要求:
性質 1:每個節點要么是紅色,要么是黑色。
性質 2:根節點永遠是黑色的。
性質 3:所有的葉節點都是空節點(即 null),并且是黑色的。
性質 4:每個紅色節點的兩個子節點都是黑色。(從每個葉子到根的路徑上不會有兩個連續的紅色節點)
性質 5:從任一節點到其子樹中每個葉子節點的路徑都包含相同數量的黑色節點。
下圖展示了一個紅黑樹,其中白色節點代表紅色。
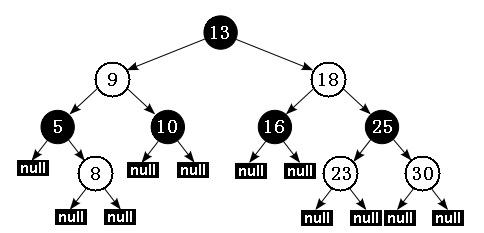
根據性質 5:紅黑樹從根節點到每個葉子節點的路徑都包含相同數量的黑色節點,因此從根節點到葉子節點的路徑中包含的黑色節點數被稱為樹的“黑色高度(black-height)”。 性質 4 則保證了從根節點到葉子節點的最長路徑的長度不會超過任何其他路徑的兩倍。假如有一棵黑色高度為 3 的紅黑樹:從根節點到葉節點的最短路徑長度是 2,該路徑上全是黑色節點(黑節點 - 黑節點 - 黑節點)。最長路徑也只可能為 4,在每個黑色節點之間插入一個紅色節點(黑節點 - 紅節點 - 黑節點 - 紅節點 - 黑節點),性質 4 保證絕不可能插入更多的紅色節點。由此可見,紅黑樹中最長路徑就是一條紅黑交替的路徑。
由此我們可以得出結論:對于給定的黑色高度為 N?的紅黑樹,從根到葉子節點的最短路徑長度為 N-1,最長路徑長度為 2 * (N-1)。
紅黑樹通過上面這種限制來保證它大致是平衡的——因為紅黑樹的高度不會無限增高,這樣保證紅黑樹在最壞情況下都是高效的,不會出現普通排序二叉樹的情況。
在紅黑樹上進行插入操作和刪除操作會導致樹不再符合紅黑樹的特征,因此插入操作和刪除操作都需要進行一定的維護,以保證插入節點、刪除節點后的樹依然是紅黑樹。這也是我們在閱讀TreeMap源碼的時候需要著重關注的部分。
先來看一下TreeMap的定義:
public?class?TreeMap<K,V> ????extends?AbstractMap<K,V> ????implements?NavigableMap<K,V>,?Cloneable,?java.io.Serializable
這里可以看到,TreeMap實現了一個NavigableMap<K,V>接口,該接口定義如下:
public?interface?NavigableMap<K,V>?extends?SortedMap<K,V>
其繼承自SortedMap<K,V>,該接口定義如下:
public?interface?SortedMap<K,V>?extends?Map<K,V>
顧名思義,SortedMap定義了有序的Map,這個順序一般是指由Comparable接口提供的keys的自然序(natural ordering),也可以在創建SortedMap實例時,指定一個Comparator來決定Map的遍歷順序。
當我們在用集合視角(collection views,與HashMap一樣,也是由entrySet、keySet與values方法提供)來迭代(iterate)一個SortedMap實例時會體現出key的順序。
再申明一下關于Comparable與Comparator的區別:
Comparable一般表示類的自然序,比如定義一個Student類,學號為默認排序;
Comparator一般表示類在某種場合下的特殊分類,需要定制化排序。比如現在想按照Student類的age來排序。
插入SortedMap中的key的類都必須繼承Comparable類(或指定一個comparator),這樣才能確定如何比較(通過k1.compareTo(k2)或comparator.compare(k1, k2))兩個key,否則,在插入時,會報ClassCastException的異常。
此外,SortedMap中key的順序性應與equals方法保持一致。也就是說k1.compareTo(k2)或comparator.compare(k1, k2)為true時,k1.equals(k2)也應該為true。
介紹完了SortedMap,現在再回到NavigableMap<K,V>上來。
NavigableMap出現于JDK 1.6,它在SortedMap的基礎上,增加了一些“導航方法”(navigation methods)來返回與搜索目標最近的元素。例如:
lowerEntry,返回所有比給定Map.Entry小的元素
floorEntry,返回所有比給定Map.Entry小或相等的元素
ceilingEntry,返回所有比給定Map.Entry大或相等的元素
higherEntry,返回所有比給定Map.Entry大的元素
先來看一下TreeMap的靜態內部類Entry,它實現了紅黑樹的節點:
???static?final?class?Entry<K,V>?implements?Map.Entry<K,V>?{
????????K?key;
????????V?value;
????????Entry<K,V>?left;
????????Entry<K,V>?right;
????????Entry<K,V>?parent;
????????//節點默認為黑色????????boolean?color?=?BLACK;
????????/**?*?傳入key,value,parent參數,創建新節點,子樹為null,節點顏色默認為黑色。?*/
????????Entry(K?key,?V?value,?Entry<K,V>?parent)?{
????????????this.key?=?key;
????????????this.value?=?value;
????????????this.parent?=?parent;
????????}
????????/**?*?Returns?the?key.?*?*?@return?the?key?*/
????????public?K?getKey()?{
????????????return?key;
????????}
????????/**?*?Returns?the?value?associated?with?the?key.?*?*?@return?the?value?associated?with?the?key?*/
????????public?V?getValue()?{
????????????return?value;
????????}
????????/**?*?Replaces?the?value?currently?associated?with?the?key?with?the?given?*?value.?*?*?@return?the?value?associated?with?the?key?before?this?method?was?*?called?*/
????????public?V?setValue(V?value)?{
????????????V?oldValue?=?this.value;
????????????this.value?=?value;
????????????return?oldValue;
????????}
????????public?boolean?equals(Object?o)?{
????????????if?(!(o?instanceof?Map.Entry))
????????????????return?false;
????????????Map.Entry<?,?>?e?=?(Map.Entry<?,?>)o;
????????????return?valEquals(key,e.getKey())?&&?valEquals(value,e.getValue());
????????}
????????public?int?hashCode()?{
????????????int?keyHash?=?(key==null???0?:?key.hashCode());
????????????int?valueHash?=?(value==null???0?:?value.hashCode());
????????????return?keyHash?^?valueHash;
????????}
????????public?String?toString()?{
????????????return?key?+?"="?+?value;
????????}
????}從代碼中可以看出,一個Entry對象代表了紅黑樹的一個節點,其中除了存放著key-value pair的key、value值,還存放著該節點的顏色、左子節點、右子節點、父節點。
再來看一下TreeMap的重要屬性:
????//用來它定制排序規則,當它的值為null時,則使用key的自然順序排序????private?final?Comparator<??super?K>?comparator; ????//紅黑樹的根節點????private?transient?Entry<K,V>?root; ????/**?*?The?number?of?entries?in?the?tree?*/ ????private?transient?int?size?=?0; ????/**?*?The?number?of?structural?modifications?to?the?tree.?*/ ????private?transient?int?modCount?=?0;
下面來看一下TreeMap中最常用的增刪改查方法,它們的源碼都很好地體現了紅黑樹的特點。
put方法可以將一對key-value pair放到TreeMap中,當然也可以修改TreeMap中某個key對應的value值。在內部實現中,也需要將一個節點添加到紅黑樹中,這改變了原有紅黑樹的結構,因此需要做一些調整來保證修改后的樹也符合紅黑樹的規則,讓我們來看看源碼中是怎么做的:
??public?V?put(K?key,?V?value)?{
????????Entry<K,V>?t?=?root;
????????if?(t?==?null)?{
????????????compare(key,?key);?//?type?(and?possibly?null)?check
????????????root?=?new?Entry<>(key,?value,?null);
????????????size?=?1;
????????????modCount++;
????????????return?null;
????????}
????????int?cmp;
????????Entry<K,V>?parent;
????????//?split?comparator?and?comparable?paths????????Comparator<??super?K>?cpr?=?comparator;
????????if?(cpr?!=?null)?{
????????????do?{
????????????????parent?=?t;
????????????????cmp?=?cpr.compare(key,?t.key);
????????????????if?(cmp?<?0)
????????????????????t?=?t.left;
????????????????else?if?(cmp?>?0)
????????????????????t?=?t.right;
????????????????else
????????????????????return?t.setValue(value);
????????????}?while?(t?!=?null);
????????}
????????else?{
????????????if?(key?==?null)
????????????????throw?new?NullPointerException();
????????????@SuppressWarnings("unchecked")
????????????????Comparable<??super?K>?k?=?(Comparable<??super?K>)?key;
????????????do?{
????????????????parent?=?t;
????????????????cmp?=?k.compareTo(t.key);
????????????????if?(cmp?<?0)
????????????????????t?=?t.left;
????????????????else?if?(cmp?>?0)
????????????????????t?=?t.right;
????????????????else
????????????????????return?t.setValue(value);
????????????}?while?(t?!=?null);
????????}
????????Entry<K,V>?e?=?new?Entry<>(key,?value,?parent);
????????if?(cmp?<?0)
????????????parent.left?=?e;
????????else
????????????parent.right?=?e;
????????fixAfterInsertion(e);
????????size++;
????????modCount++;
????????return?null;
????}put方法就是將新的Entry添加到二叉排序樹上的過程,內容并不復雜,需要額外關注的是它調用的fixAfterInsertion(e)方法,該方法就是修復紅黑樹的過程,其源碼如下,筆者已進行了詳細地注釋:
????private?void?fixAfterInsertion(Entry<K,V>?x)?{
????????x.color?=?RED;
//?直到?x?節點的父節點不是根,且?x?的父節點不是紅色????????while?(x?!=?null?&&?x?!=?root?&&?x.parent.color?==?RED)?{
????????????//?如果?x?的父節點是其父節點的左子節點????????????if?(parentOf(x)?==?leftOf(parentOf(parentOf(x))))?{
????????????????//?獲取?x?的父節點的兄弟節點????????????????Entry<K,V>?y?=?rightOf(parentOf(parentOf(x)));
????????????????//?如果?x?的父節點的兄弟節點是紅色????????????????if?(colorOf(y)?==?RED)?{
????????????????????//?將?x?的父節點設為黑色????????????????????setColor(parentOf(x),?BLACK);
????????????????????//?將?x?的父節點的兄弟節點設為黑色????????????????????setColor(y,?BLACK);
????????????????????//?將?x?的父節點的父節點設為紅色????????????????????setColor(parentOf(parentOf(x)),?RED);
????????????????????x?=?parentOf(parentOf(x));
????????????????}?else?{//?如果?x?的父節點的兄弟節點是黑色????????????????????//?如果?x?是其父節點的右子節點????????????????????if?(x?==?rightOf(parentOf(x)))?{
????????????????????????//?將?x?的父節點設為?x????????????????????????x?=?parentOf(x);
????????????????????????rotateLeft(x);
????????????????????}
????????????????????//?把?x?的父節點設為黑色????????????????????setColor(parentOf(x),?BLACK);
????????????????????//?把?x?的父節點的父節點設為紅色????????????????????setColor(parentOf(parentOf(x)),?RED);
????????????????????rotateRight(parentOf(parentOf(x)));
????????????????}
????????????}?else?{//?如果?x?的父節點是其父節點的右子節點????????????????//?獲取?x?的父節點的兄弟節點????????????????Entry<K,V>?y?=?leftOf(parentOf(parentOf(x)));
????????????????//?如果?x?的父節點的兄弟節點是紅色????????????????if?(colorOf(y)?==?RED)?{
????????????????????//?將?x?的父節點設為黑色????????????????????setColor(parentOf(x),?BLACK);
????????????????????//?將?x?的父節點的兄弟節點設為黑色????????????????????setColor(y,?BLACK);
????????????????????//?將?x?的父節點的父節點設為紅色????????????????????setColor(parentOf(parentOf(x)),?RED);
????????????????????//?將?x?設為?x?的父節點的節點????????????????????x?=?parentOf(parentOf(x));
????????????????}?else?{//?如果?x?的父節點的兄弟節點是黑色????????????????????//?如果?x?是其父節點的左子節點????????????????????if?(x?==?leftOf(parentOf(x)))?{
????????????????????????//?將?x?的父節點設為?x?
????????????????????????x?=?parentOf(x);
????????????????????????rotateRight(x);
????????????????????}
????????????????????//?把?x?的父節點設為黑色????????????????????setColor(parentOf(x),?BLACK);
????????????????????//?把?x?的父節點的父節點設為紅色????????????????????setColor(parentOf(parentOf(x)),?RED);
????????????????????rotateLeft(parentOf(parentOf(x)));
????????????????}
????????????}
????????}
????????//?將根節點設為黑色????????root.color?=?BLACK;
????}remove(key)方法就是從TreeMap中刪除一對key-pair,也就是從紅黑樹中刪除一個節點,進行該操作后也需要修復紅黑樹,具體代碼如下:
public?V?remove(Object?key)?{
????????Entry<K,V>?p?=?getEntry(key);
????????if?(p?==?null)
????????????return?null;
????????V?oldValue?=?p.value;
????????deleteEntry(p);
????????return?oldValue;
????}其中調用的deleteEntry方法,主要作用就是將指定的Entry從紅黑樹中刪除,源碼如下:
???private?void?deleteEntry(Entry<K,V>?p)?{
????????modCount++;
????????size--;
????????//?If?strictly?internal,?copy?successor's?element?to?p?and?then?make?p????????//?point?to?successor.????????if?(p.left?!=?null?&&?p.right?!=?null)?{
????????????Entry<K,V>?s?=?successor(p);
????????????p.key?=?s.key;
????????????p.value?=?s.value;
????????????p?=?s;
????????}?//?p?has?2?children
????????//?Start?fixup?at?replacement?node,?if?it?exists.????????Entry<K,V>?replacement?=?(p.left?!=?null???p.left?:?p.right);
????????if?(replacement?!=?null)?{
????????????//?Link?replacement?to?parent????????????replacement.parent?=?p.parent;
????????????if?(p.parent?==?null)
????????????????root?=?replacement;
????????????else?if?(p?==?p.parent.left)
????????????????p.parent.left??=?replacement;
????????????else
????????????????p.parent.right?=?replacement;
????????????//?Null?out?links?so?they?are?OK?to?use?by?fixAfterDeletion.????????????p.left?=?p.right?=?p.parent?=?null;
????????????//?Fix?replacement????????????if?(p.color?==?BLACK)
????????????????fixAfterDeletion(replacement);
????????}?else?if?(p.parent?==?null)?{?//?return?if?we?are?the?only?node.????????????root?=?null;
????????}?else?{?//?No?children.?Use?self?as?phantom?replacement?and?unlink.????????????if?(p.color?==?BLACK)
????????????????fixAfterDeletion(p);
????????????if?(p.parent?!=?null)?{
????????????????if?(p?==?p.parent.left)
????????????????????p.parent.left?=?null;
????????????????else?if?(p?==?p.parent.right)
????????????????????p.parent.right?=?null;
????????????????p.parent?=?null;
????????????}
????????}
????}這段代碼邏輯并不復雜,但在完成刪除后,也需要調用一個fixAfterDeletion,來修復紅黑樹的結構,代碼如下:
//?刪除節點后修復紅黑樹private?void?fixAfterDeletion(Entry<K,V>?x)?{?
???//?直到?x?不是根節點,且?x?的顏色是黑色???while?(x?!=?root?&&?colorOf(x)?==?BLACK)?
???{?
???????//?如果?x?是其父節點的左子節點???????if?(x?==?leftOf(parentOf(x)))?
???????{?
???????????//?獲取?x?節點的兄弟節點???????????Entry<K,V>?sib?=?rightOf(parentOf(x));?
???????????//?如果?sib?節點是紅色???????????if?(colorOf(sib)?==?RED)?
???????????{?
???????????????//?將?sib?節點設為黑色???????????????setColor(sib,?BLACK);?
???????????????//?將?x?的父節點設為紅色???????????????setColor(parentOf(x),?RED);?
???????????????rotateLeft(parentOf(x));?
???????????????//?再次將?sib?設為?x?的父節點的右子節點???????????????sib?=?rightOf(parentOf(x));?
???????????}?
???????????//?如果?sib?的兩個子節點都是黑色???????????if?(colorOf(leftOf(sib))?==?BLACK?
???????????????&&?colorOf(rightOf(sib))?==?BLACK)?
???????????{?
???????????????//?將?sib?設為紅色???????????????setColor(sib,?RED);?
???????????????//?讓?x?等于?x?的父節點???????????????x?=?parentOf(x);?
???????????}?
???????????else?
???????????{?
???????????????//?如果?sib?的只有右子節點是黑色???????????????if?(colorOf(rightOf(sib))?==?BLACK)?
???????????????{?
???????????????????//?將?sib?的左子節點也設為黑色???????????????????setColor(leftOf(sib),?BLACK);?
???????????????????//?將?sib?設為紅色???????????????????setColor(sib,?RED);?
???????????????????rotateRight(sib);?
???????????????????sib?=?rightOf(parentOf(x));?
???????????????}?
???????????????//?設置?sib?的顏色與?x?的父節點的顏色相同???????????????setColor(sib,?colorOf(parentOf(x)));?
???????????????//?將?x?的父節點設為黑色???????????????setColor(parentOf(x),?BLACK);?
???????????????//?將?sib?的右子節點設為黑色???????????????setColor(rightOf(sib),?BLACK);?
???????????????rotateLeft(parentOf(x));?
???????????????x?=?root;?
???????????}?
???????}?
???????//?如果?x?是其父節點的右子節點???????else?
???????{?
???????????//?獲取?x?節點的兄弟節點???????????Entry<K,V>?sib?=?leftOf(parentOf(x));?
???????????//?如果?sib?的顏色是紅色???????????if?(colorOf(sib)?==?RED)?
???????????{?
???????????????//?將?sib?的顏色設為黑色???????????????setColor(sib,?BLACK);?
???????????????//?將?sib?的父節點設為紅色???????????????setColor(parentOf(x),?RED);?
???????????????rotateRight(parentOf(x));?
???????????????sib?=?leftOf(parentOf(x));?
???????????}?
???????????//?如果?sib?的兩個子節點都是黑色???????????if?(colorOf(rightOf(sib))?==?BLACK?
???????????????&&?colorOf(leftOf(sib))?==?BLACK)?
???????????{?
???????????????//?將?sib?設為紅色???????????????setColor(sib,?RED);?
???????????????//?讓?x?等于?x?的父節點???????????????x?=?parentOf(x);?
???????????}?
???????????else?
???????????{?
???????????????//?如果?sib?只有左子節點是黑色???????????????if?(colorOf(leftOf(sib))?==?BLACK)?
???????????????{?
???????????????????//?將?sib?的右子節點也設為黑色???????????????????setColor(rightOf(sib),?BLACK);?
???????????????????//?將?sib?設為紅色???????????????????setColor(sib,?RED);?
???????????????????rotateLeft(sib);?
???????????????????sib?=?leftOf(parentOf(x));?
???????????????}?
???????????????//?將?sib?的顏色設為與?x?的父節點顏色相同???????????????setColor(sib,?colorOf(parentOf(x)));?
???????????????//?將?x?的父節點設為黑色???????????????setColor(parentOf(x),?BLACK);?
???????????????//?將?sib?的左子節點設為黑色???????????????setColor(leftOf(sib),?BLACK);?
???????????????rotateRight(parentOf(x));?
???????????????x?=?root;?
???????????}?
???????}?
???}?
???setColor(x,?BLACK);?}get(key)方法是通過傳入的key值來查找其對應的value,這一操作并不會改變紅黑樹的結構,源碼如下:
public?V?get(Object?key)?{?
???//?根據指定?key?取出對應的?Entry?
???Entry>K,V<?p?=?getEntry(key);?
???//?返回該?Entry?所包含的?value?
???return?(p==null???null?:?p.value);?}其調用了getEntry(key)方法,該方法源碼如下:
final?Entry<K,V>?getEntry(Object?key)?{?
???//?如果?comparator?不為?null,表明程序采用定制排序???if?(comparator?!=?null)?
???????//?調用?getEntryUsingComparator?方法來取出對應的?key?
???????return?getEntryUsingComparator(key);?
???//?如果?key?形參的值為?null,拋出?NullPointerException?異常???if?(key?==?null)?
???????throw?new?NullPointerException();?
???//?將?key?強制類型轉換為?Comparable?實例???Comparable<??super?K>?k?=?(Comparable<??super?K>)?key;?
???//?從樹的根節點開始???Entry<K,V>?p?=?root;?
???while?(p?!=?null)?
???{?
???????//?拿?key?與當前節點的?key?進行比較???????int?cmp?=?k.compareTo(p.key);?
???????//?如果?key?小于當前節點的?key,向“左子樹”搜索???????if?(cmp?<?0)?
???????????p?=?p.left;?
???????//?如果?key?大于當前節點的?key,向“右子樹”搜索???????else?if?(cmp?>?0)?
???????????p?=?p.right;?
???????//?不大于、不小于,就是找到了目標?Entry?
???????else?
???????????return?p;?
???}?
???return?null;?}該方法思路很簡單,就是利用排序二叉樹的特征來搜索key值對應的Entry,從二叉樹的根節點開始,如果被搜索節點大于當前節點,程序向“右子樹”搜索;如果被搜索節點小于當前節點,程序向“左子樹”搜索;如果相等,那就是找到了指定節點。
此外,該方法中需要考慮用Comparator定制排序或用key的自然順序排序兩種情況,當comparator != null?即采用定制排序,此時就要調用?getEntryUsingComparator(key)方法:
final?Entry<K,V>?getEntryUsingComparator(Object?key)?{?
???K?k?=?(K)?key;?
???//?獲取該?TreeMap?的?comparator?
???Comparator<??super?K>?cpr?=?comparator;?
???if?(cpr?!=?null)?
???{?
???????//?從根節點開始???????Entry<K,V>?p?=?root;?
???????while?(p?!=?null)?
???????{?
???????????//?拿?key?與當前節點的?key?進行比較???????????int?cmp?=?cpr.compare(k,?p.key);?
???????????//?如果?key?小于當前節點的?key,向“左子樹”搜索???????????if?(cmp?<?0)?
???????????????p?=?p.left;?
???????????//?如果?key?大于當前節點的?key,向“右子樹”搜索???????????else?if?(cmp?>?0)?
???????????????p?=?p.right;?
???????????//?不大于、不小于,就是找到了目標?Entry?
???????????else?
???????????????return?p;?
???????}?
???}?
???return?null;?}其具體實現與getEntry方法相似,只是排序方法不同。
TreeMap內部用紅黑樹保存數據,迭代順序按照key值有序,與HashMap相比效率更低,只建議在需要按序索引key值時使用,它也是非線程安全的,key和value均不能為null值。
本文是該系列的最后一篇文章,在系列文章中我們重點介紹了List接口和Map接口的幾個實現類,關于Set接口,它的特點是存儲內容不能重復,我們知道Map接口定義的key-value pair中的key也是不能重復的,因此可以將Map接口實現類的value用一個未賦初值的Object對象代替,即能作為Set接口的實現。實際上Set接口有三個實現類HashSet、LinkedHashSet和TreeSet,它們在底層就是分別用HashMap、LinkedHashMap、TreeMap實現的。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。