您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了怎么使用Python繪制分形圖案的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇怎么使用Python繪制分形圖案文章都會有所收獲,下面我們一起來看看吧。
寫一個可以畫等邊三角形的程序,并且在三角形的每條邊上,它必須能夠繪制一個稍微小一點的向外的三角形。能夠根據人的意愿多次重復此過程,從而創建一些有趣的模式。
把圖像表示為一個二維的像素陣列。像素陣列中的每個單元格將代表該像素的顏色(RGB)。
為此,可以使用NumPy庫生成像素數組,并使用Pillow將其轉換為可以保存的圖像。
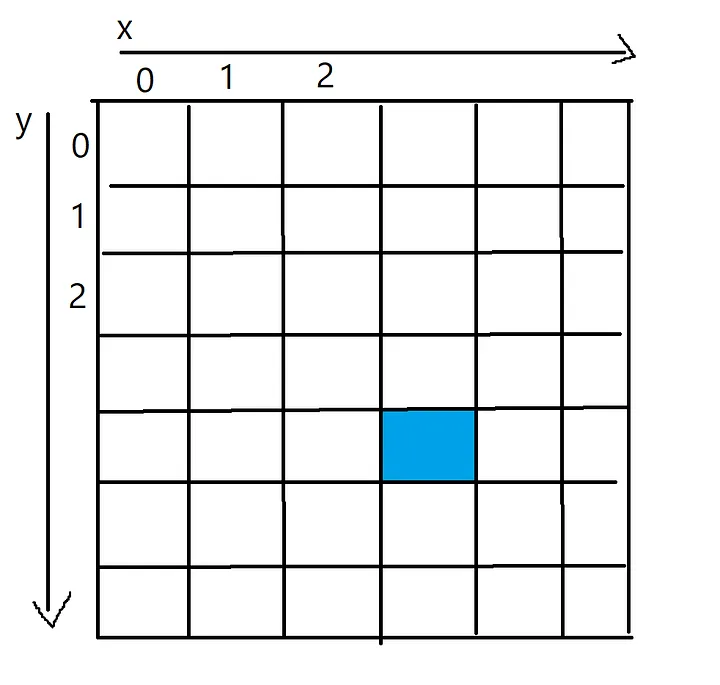
藍色像素的x值為3,y值為4,可以通過一個二維數組訪問,如pixels[4][3]
現在開始編碼,首先,需要一個可以獲取兩組坐標并在它們之間畫一條線的函數。
下面的代碼通過在兩點之間插值來工作,每一步都向像素陣列添加新的像素。你可以把這個過程看作是在一條線上逐個像素地進行著色。
可以在每個代碼片段中使用連續字符“\”來容納一些較長的代碼行。
import numpy as np
from PIL import Image
import math
def plot_line(from_coordinates, to_coordinates, thickness, colour, pixels):
# 找出像素陣列的邊界
max_x_coordinate = len(pixels[0])
max_y_coordinate = len(pixels)
# 兩點之間沿著x軸和y軸的距離
horizontal_distance = to_coordinates[1] - from_coordinates[1]
vertical_distance = to_coordinates[0] - from_coordinates[0]
# 兩點之間的總距離
distance = math.sqrt((to_coordinates[1] - from_coordinates[1])**2 \
+ (to_coordinates[0] - from_coordinates[0])**2)
# 每次給一個新的像素上色時,將向前走多遠
horizontal_step = horizontal_distance/distance
vertical_step = vertical_distance/distance
# 此時,將進入循環以在像素數組中繪制線
# 循環的每一次迭代都會沿著線添加一個新的點
for i in range(round(distance)):
# 這兩個坐標是直線中心的坐標
current_x_coordinate = round(from_coordinates[1] + (horizontal_step*i))
current_y_coordinate = round(from_coordinates[0] + (vertical_step*i))
# 一旦得到了點的坐標,
# 就在坐標周圍畫出尺寸為thickness的圖案
for x in range (-thickness, thickness):
for y in range (-thickness, thickness):
x_value = current_x_coordinate + x
y_value = current_y_coordinate + y
if (x_value > 0 and x_value < max_x_coordinate and \
y_value > 0 and y_value < max_y_coordinate):
pixels[y_value][x_value] = colour
# 定義圖像的大小
pixels = np.zeros( (500,500,3), dtype=np.uint8 )
# 畫一條線
plot_line([0,0], [499,499], 1, [255,200,0], pixels)
# 把像素陣列變成一張真正的圖片
img = Image.fromarray(pixels)
# 顯示得到的圖片,并保存它
img.show()
img.save('Line.png')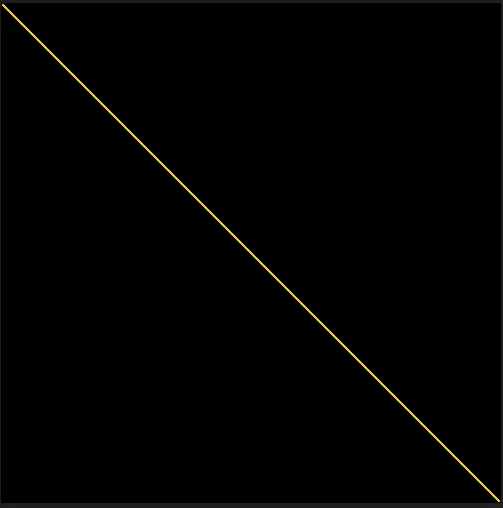
此函數在像素陣列的每個角之間繪制一條黃線時的結果
現在有了一個可以在兩點之間畫線的函數,可以畫第一個等邊三角形了。
給定三角形的中心點和邊長,可以使用公式計算出高度:h = ½(√3a)。
現在利用這個高度、中心點和邊長,可以計算出三角形的每個角的位置。使用之前制作的plot_line函數,可以在每個角之間畫一條線。
def draw_triangle(center, side_length, thickness, colour, pixels): # 等邊三角形的高度是,h = ?(√3a) # 其中a是邊長 triangle_height = round(side_length * math.sqrt(3)/2) # 頂角 top = [center[0] - triangle_height/2, center[1]] # 左下角 bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2] # 右下角 bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2] # 在每個角之間畫一條線來完成三角形 plot_line(top, bottom_left, thickness, colour, pixels) plot_line(top, bottom_right, thickness, colour, pixels) plot_line(bottom_left, bottom_right, thickness, colour, pixels)

在500x500像素PNG的中心繪制三角形時的結果
一切都已準備就緒,可以用Python創建第一個分形。
但是最后一步是最難完成的,三角形函數為它的每一邊調用自己,需要能夠計算每個新的較小三角形的中心點,并正確地旋轉它們,使它們垂直于它們所附著的一側。
通過從旋轉的坐標中減去中心點的偏移量,然后應用公式來旋轉一對坐標,可以用這個函數來旋轉三角形的每個角。
def rotate(coordinate, center_point, degrees): # 從坐標中減去旋轉的點 x = (coordinate[0] - center_point[0]) y = (coordinate[1] - center_point[1]) # Python的cos和sin函數采用弧度而不是度數 radians = math.radians(degrees) # 計算旋轉點 new_x = (x * math.cos(radians)) - (y * math.sin(radians)) new_y = (y * math.cos(radians)) + (x * math.sin(radians)) # 將在開始時減去的偏移量加回旋轉點上 return [new_x + center_point[0], new_y + center_point[1]]

將每個坐標旋轉35度的三角形
可以旋轉一個三角形后,思考如何在第一個三角形的每條邊上畫一個新的小三角形。
為了實現這一點,擴展draw_triangle函數,為每條邊計算一個新三角形的旋轉和中心點,其邊長被參數shrink_side_by減少。
一旦它計算出新三角形的中心點和旋轉,它就會調用draw_triangle(自身)來從當前線的中心畫出新的、更小的三角形。然后,這將反過來打擊同一個代碼塊,為一個更小的三角形計算另一組中心點和旋轉。
這就是所謂的循環算法,因為draw_triangle函數現在會調用自己,直到達到希望繪制的三角形的最大深度。有這個轉義句子是很重要的,因為理論上這個函數會一直循環下去(但實際上調用堆棧會變得太大,導致堆棧溢出錯誤)。
def draw_triangle(center, side_length, degrees_rotate, thickness, colour, \ pixels, shrink_side_by, iteration, max_depth): # 等邊三角形的高度是,h = ?(√3a) # 其中'a'是邊長 triangle_height = side_length * math.sqrt(3)/2 # 頂角 top = [center[0] - triangle_height/2, center[1]] # 左下角 bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2] # 右下角 bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2] if (degrees_rotate != 0): top = rotate(top, center, degrees_rotate) bottom_left = rotate(bottom_left, center, degrees_rotate) bottom_right = rotate(bottom_right, center, degrees_rotate) # 三角形各邊之間的坐標 lines = [[top, bottom_left],[top, bottom_right],[bottom_left, bottom_right]] line_number = 0 # 在每個角之間畫一條線來完成三角形 for line in lines: line_number += 1 plot_line(line[0], line[1], thickness, colour, pixels) # 如果還沒有達到max_depth,就畫一些新的三角形 if (iteration < max_depth and (iteration < 1 or line_number < 3)): gradient = (line[1][0] - line[0][0]) / (line[1][1] - line[0][1]) new_side_length = side_length*shrink_side_by # 正在繪制的三角形線的中心 center_of_line = [(line[0][0] + line[1][0]) / 2, \ (line[0][1] + line[1][1]) / 2] new_center = [] new_rotation = degrees_rotate # 需要旋轉traingle的數量 if (line_number == 1): new_rotation += 60 elif (line_number == 2): new_rotation -= 60 else: new_rotation += 180 # 在一個理想的世界里,這將是gradient=0, # 但由于浮點除法的原因,無法 # 確保永遠是這種情況 if (gradient < 0.0001 and gradient > -0.0001): if (center_of_line[0] - center[0] > 0): new_center = [center_of_line[0] + triangle_height * \ (shrink_side_by/2), center_of_line[1]] else: new_center = [center_of_line[0] - triangle_height * \ (shrink_side_by/2), center_of_line[1]] else: # 計算直線梯度的法線 difference_from_center = -1/gradient # 計算這條線距中心的距離 # 到新三角形的中心 distance_from_center = triangle_height * (shrink_side_by/2) # 計算 x 方向的長度, # 從線的中心到新三角形的中心 x_length = math.sqrt((distance_from_center**2)/ \ (1 + difference_from_center**2)) # 計算出x方向需要走哪條路 if (center_of_line[1] < center[1] and x_length > 0): x_length *= -1 # 現在計算Y方向的長度 y_length = x_length * difference_from_center # 用新的x和y值來偏移線的中心 new_center = [center_of_line[0] + y_length, \ center_of_line[1] + x_length] draw_triangle(new_center, new_side_length, new_rotation, \ thickness, colour, pixels, shrink_side_by, \ iteration+1, max_depth)

三角形分形,收縮邊=1/2,最大深度=2
關于“怎么使用Python繪制分形圖案”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“怎么使用Python繪制分形圖案”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。