Python曲線擬合怎么實現

今天小編給大家分享一下Python曲線擬合怎么實現的相關知識點，內容詳細，邏輯清晰，相信大部分人都還太了解這方面的知識，所以分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后有所收獲，下面我們一起來了解一下吧。

入門

scipy.optimize中，curve_fit函數可調用非線性最小二乘法進行函數擬合，例如，現在有一個高斯函數想要被擬合

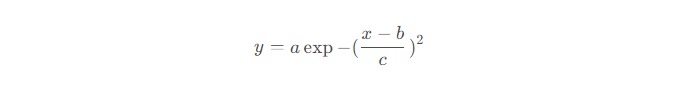
則調用方法如下

import numpy as np
from scipy.optimize import curve_fit
def gauss(x, a, b, c):
    return a*np.exp(-(x-b)**2/c**2)

x = np.arange(100)/10
y = gauss(x, 2, 5, 3) + np.random.rand(100)/10

# 非線性擬合 abc為參數；para為擬合評價
abc, para = curve_fit(gauss, x, y)
print(abc)
# [2.03042233 5.01182397 3.10994351]

其中，curve_fit在調用時輸入了三個參數，分別是擬合函數、自變量、因變量。返回值abc和para分別為擬合參數和擬合的協方差，最終得到abc的值與預設的2,0.5, 3是比較接近的，其擬合效果可以畫圖查看一下

import matplotlib.pyplot as plt
plt.scatter(x, y, marker='.')

Y = gauss(x, *abc)
plt.plot(x, Y, lw=1)
plt.show()

效果如下

參數

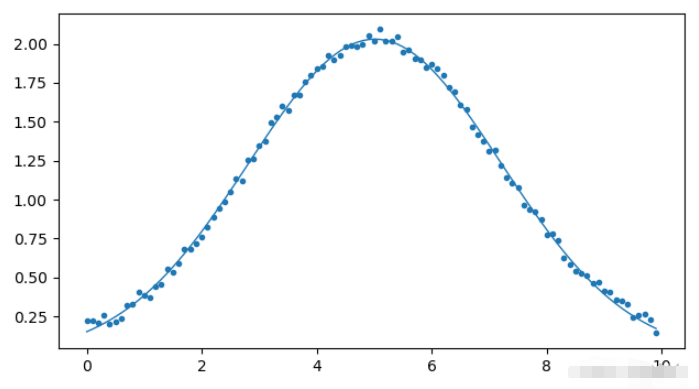
curve_fit的裝形式如下

curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=True, bounds=(-inf, inf), method=None, jac=None, *, full_output=False, **kwargs)

除了f, xdata, ydata已經用過之外，其他參數的含義為

• p0 擬合參數初始值

• sigma 相對精度要求

• absolute_sigma絕對精度要求

• check_finite有限性檢測開關

• bounds擬合范圍

• method擬合方法，可選‘lm’, ‘trf’, ‘dogbox’，與least_squares函數中定義相同

• jac雅可比矩陣，與least_squares中定義相同

 最小二乘函數：least_squares

多元擬合

盡管curve_fit的參數列表中，只給出了xdata, ydata作為擬合參數，而xdata只有一組，但curve_fit是具備多元擬合潛力的。

唯一需要注意的是，當多元擬合函數的返回值必須為一維數組，示例如下

# 創建一個函數模型用來生成數據
def func1(x, a, b, c, d):
    r = a * np.exp(-((x[0] - b) ** 2 + (x[1] - d) ** 2) / (2 * c ** 2))
    return r.ravel()
 
# 生成原始數據
xx = np.indices([10, 10])
z = func1(xx, 10, 5, 2, 5) + np.random.normal(size=100)/100
abcd, para = curve_fit(func1, xx, z)
print(abcd)
# [10.00258587  5.00146314  1.99952885  5.00138184]

可以發現擬合結果與預設的abcd還是比較接近的，下面繪制三維圖像來更加直觀地查看一下

z = z.reshape(10, 10)
Z = func1(xx, *abcd).reshape(10,10)

ax = plt.subplot(projection='3d')
ax.scatter3D(xx[0], xx[1], z, color='red')
ax.plot_surface(xx[0], xx[1], Z, cmap='rainbow')
plt.show()

結果如下

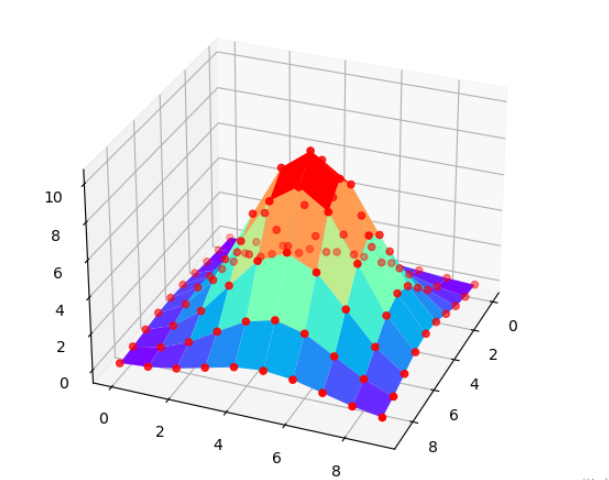
以上就是“Python曲線擬合怎么實現”這篇文章的所有內容，感謝各位的閱讀！相信大家閱讀完這篇文章都有很大的收獲，小編每天都會為大家更新不同的知識，如果還想學習更多的知識，請關注億速云行業資訊頻道。