您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
一、多項式擬合
多項式擬合的話,用的的是numpy這個庫的polyfit這個函數。那么多項式擬合,最簡單的當然是,一次多項式擬合了,就是線性回歸。直接看代碼吧
import numpy as np def linear_regression(x,y): #y=bx+a,線性回歸 num=len(x) b=(np.sum(x*y)-num*np.mean(x)*np.mean(y))/(np.sum(x*x)-num*np.mean(x)**2) a=np.mean(y)-b*np.mean(x) return np.array([b,a]) def f(x): return 2*x+1 x=np.linspace(-5,5) y=f(x)+np.random.randn(len(x))#加入噪音 y_fit=np.polyfit(x,y,1)#一次多項式擬合,也就是線性回歸 print(linear_regression(x,y)) print(y_fit)
手寫線性回歸我還是會的,然后我們來看下輸出:
[1.9937839 1.24167225]
[1.9937839 1.24167225]
由于有random每次顯示的結果都不一樣,但很明顯的是上下兩個print是意料之中的一樣,emmmmm,一次多項式擬合的源代碼應該就是像我寫的那樣。好了,那么一次以上呢?咳咳,我數學不算太好,還是老老實實用庫函數吧,順便畫下圖,見識它的威力。
import numpy as np
from matplotlib import pyplot as plt
def f(x):
return x**2+1
def f_fit(x,y_fit):
a,b,c=y_fit.tolist()
return a*x**2+b*x+c
x=np.linspace(-5,5)
y=f(x)+np.random.randn(len(x))#加入噪音
y_fit=np.polyfit(x,y,2)#二次多項式擬合
y_show=np.poly1d(y_fit)#函數優美的形式
print(y_show)#打印
y1=f_fit(x,y_fit)
plt.plot(x,f(x),'r',label='original')
plt.scatter(x,y,c='g',label='before_fitting')#散點圖
plt.plot(x,y1,'b--',label='fitting')
plt.title('polyfitting')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()#顯示標簽
plt.show()
輸出:
2
1.001 x - 0.04002 x + 0.8952
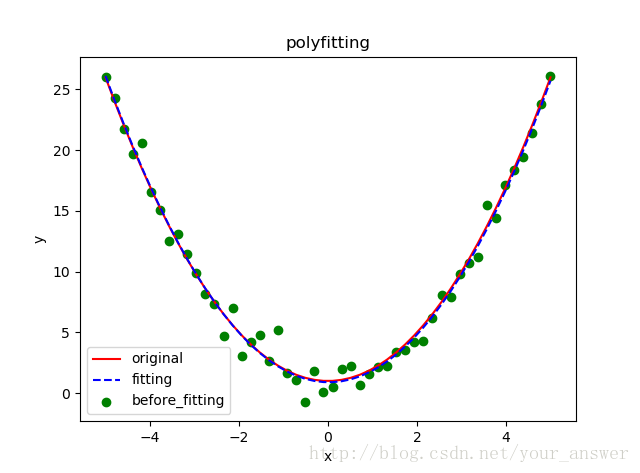
擬合效果看起來還是不錯的。
二、各種函數的擬合
一般來說,多項式的擬合就能擬合很多函數了,比如指數函數,取對數就能化為多項式函數,甚至是一次多項式函數。可是,那些三角函數之類的復雜函數不能化為多項式去擬合,怎么辦呢?要用到scipy.optimize的curve_fit函數了。
直接貼代碼:
import numpy as np
from matplotlib import pyplot as plt
from scipy.optimize import curve_fit
def f(x):
return 2*np.sin(x)+3
def f_fit(x,a,b):
return a*np.sin(x)+b
def f_show(x,p_fit):
a,b=p_fit.tolist()
return a*np.sin(x)+b
x=np.linspace(-2*np.pi,2*np.pi)
y=f(x)+0.5*np.random.randn(len(x))#加入了噪音
p_fit,pcov=curve_fit(f_fit,x,y)#曲線擬合
print(p_fit)#最優參數
print(pcov)#最優參數的協方差估計矩陣
y1=f_show(x,p_fit)
plt.plot(x,f(x),'r',label='original')
plt.scatter(x,y,c='g',label='before_fitting')#散點圖
plt.plot(x,y1,'b--',label='fitting')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
輸出:
[1.91267059 3.04489528]
[[ 9.06910892e-03 -1.83703696e-11]
[-1.83703696e-11 4.44386331e-03]]
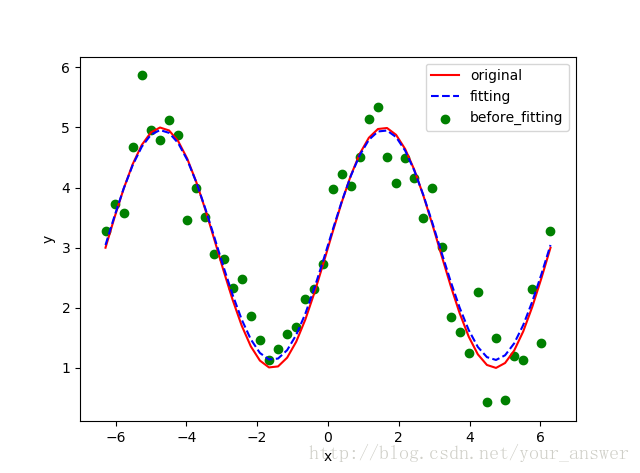
使用方法基礎的就是這樣了。然后更多詳細的參數的使用就是要看官網了。
1、https://docs.scipy.org/doc/numpy/reference/generated/numpy.polyfit.html
2、https://docs.scipy.org/doc/scipy-0.18.1/reference/generated/scipy.optimize.curve_fit.html
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。