您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“C++ RBTree紅黑樹的性質與實現方法是什么”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“C++ RBTree紅黑樹的性質與實現方法是什么”吧!
紅黑樹,是一種二叉搜索樹,但在每個結點上增加一個存儲位表示結點的顏色,可以是Red或Black。 通過對任何一條從根到葉子的路徑上各個結點著色方式的限制,紅黑樹確保沒有一條路徑會比其他路徑長出倆倍,因而是平衡的 。(既最長路徑長度不超過最短路徑長度的 2 倍)
ps:樹的路徑是從根節點走到空節點(此處為NIL 節點)才算一條路徑
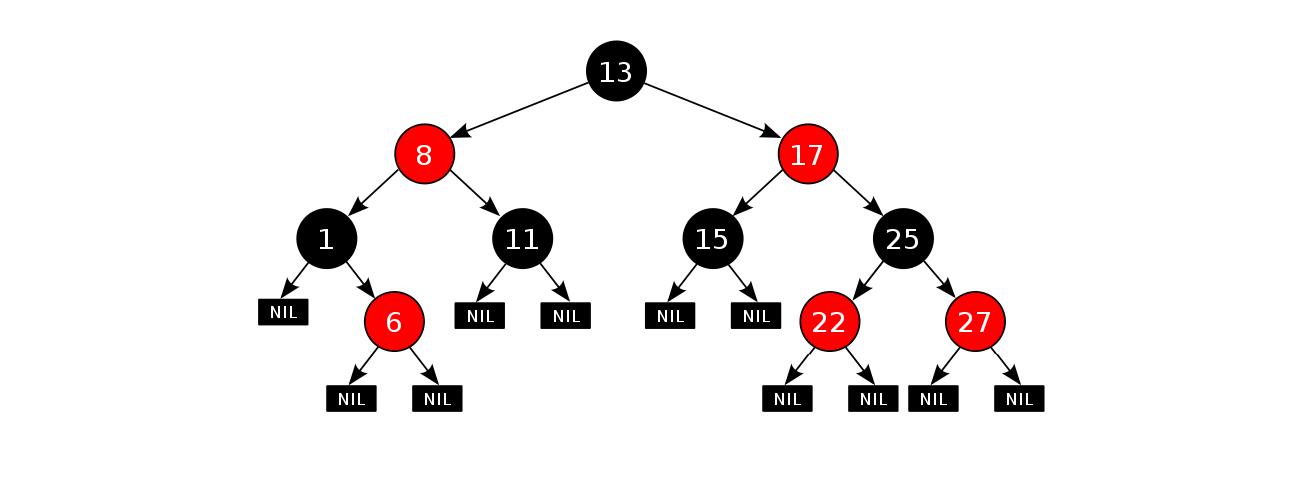
每個結點不是紅色就是黑色
根結點是黑色的
如果一個結點是紅色的,則它的兩個孩子結點是黑色的(沒有連續的紅色結點)
對于每個結點,從該節點到其所有后代葉結點的簡單路徑上,均包含相同數目的黑色結點
每個葉子結點都是黑色的(此處的葉子結點指的是空節點,NIL節點),如果是空樹,空節點也是黑色,符合第一個性質
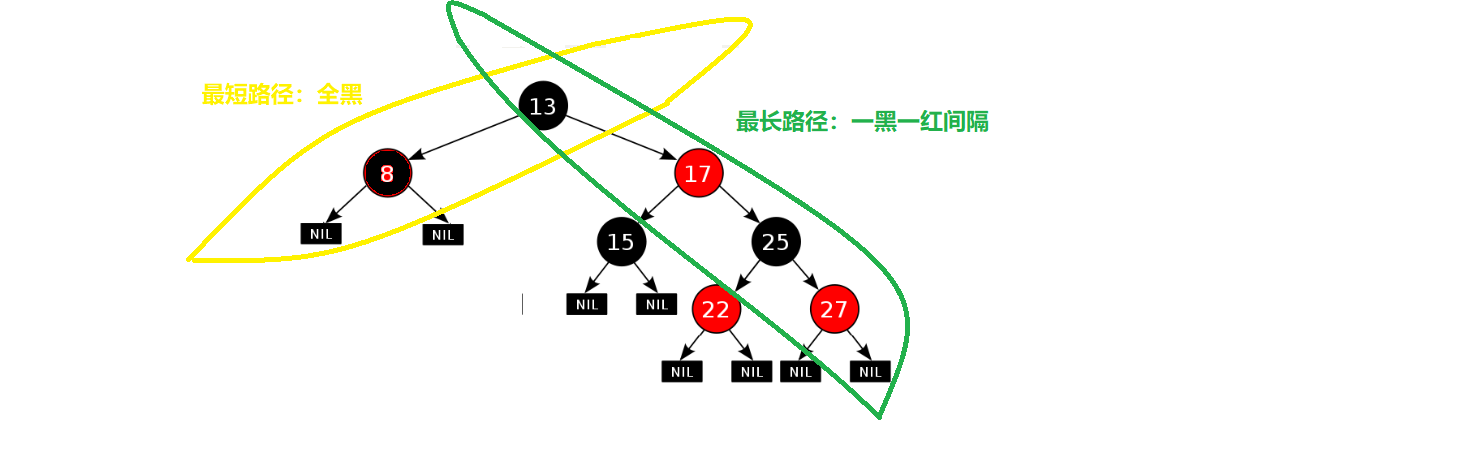
理解最長路徑長度不超過最短路徑長度的 2 倍:
根據第三個性質:紅黑樹不會出現連續的紅色結點,根據第四個性質:從每個結點到所有后代結點的路徑上包含相同數目的黑色結點。
極端場景:最短路徑上全黑,一條路徑黑色節點的數量,最長路徑上是一黑一紅相間的路徑
三叉鏈結構,對比AVL數節點的定義,把平衡因子替換成節點顏色,采用枚舉的方式:
//結點顏色
enum Color
{
RED,
BLACK,
};
template<class K, class V >
struct RBTreeNode
{
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Color _col;
RBTreeNode(const pair<K,V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_col(RED)
{}
};這里可以清楚的看到,構造結點時默認設置為紅色,問題來了:
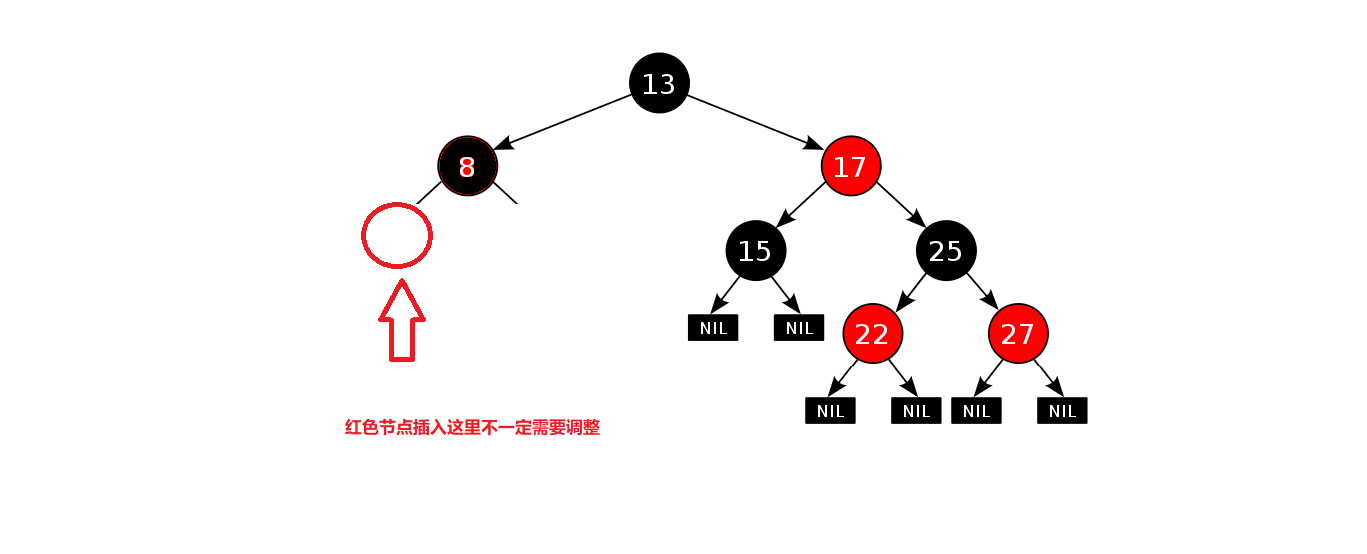
如果插入的是黑色結點那就是不符合第四個性質(路徑上均包含相同的黑色結點),此時我們必須要去進行維護每條路徑的黑色結點
如果插入的是紅色結點那就是不符合第三個性質(沒有出現連續的紅色結點),但是我們并不一定需要調整,如果根剛好為黑色,就不需要進行調整。
所以如果插入為紅色結點,不一定會破壞結構,但是如果插入黑色結點我們就必須去進行維護了
紅黑樹插入的操作部分和AVL樹的插入一樣:
找到待插入位置
將待插入結點插入到樹中
調整:若插入結點的父結點是紅色的,我們就需要對紅黑樹進行調整
前兩步大差不差
因為新節點的默認顏色是紅色,因此:如果其雙親節點的顏色是黑色,沒有違反紅黑樹任何性質,則不需要調整;但當新插入節點的雙親節點顏色為紅色時,就違反了性質三不能有連在一起的紅色節點,此時需要對紅黑樹分情況來討論
關鍵在于對紅黑樹進行調整:為了能夠展示出各種情況,這里有一個基本的模型:
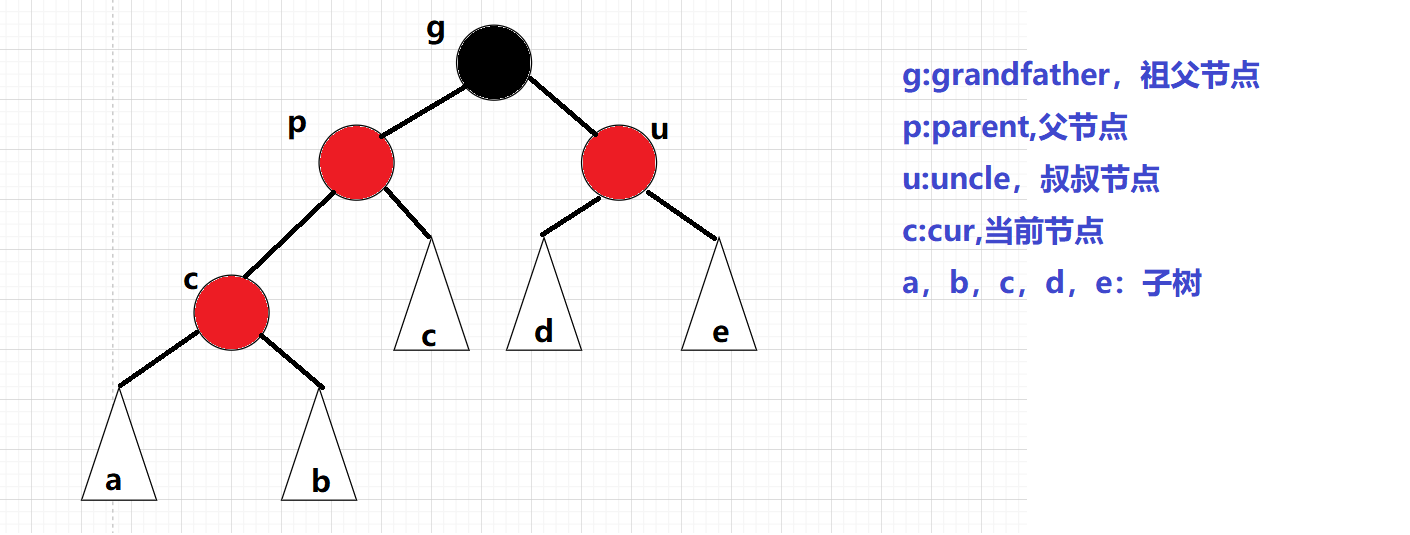
約定:cur為當前節點,p為父節點,g為祖父節點,u為叔叔節點
情況一:cur為紅,p為紅,g為黑,u存在且為紅 :
cur為紅,p為紅,g為黑,u存在且為紅
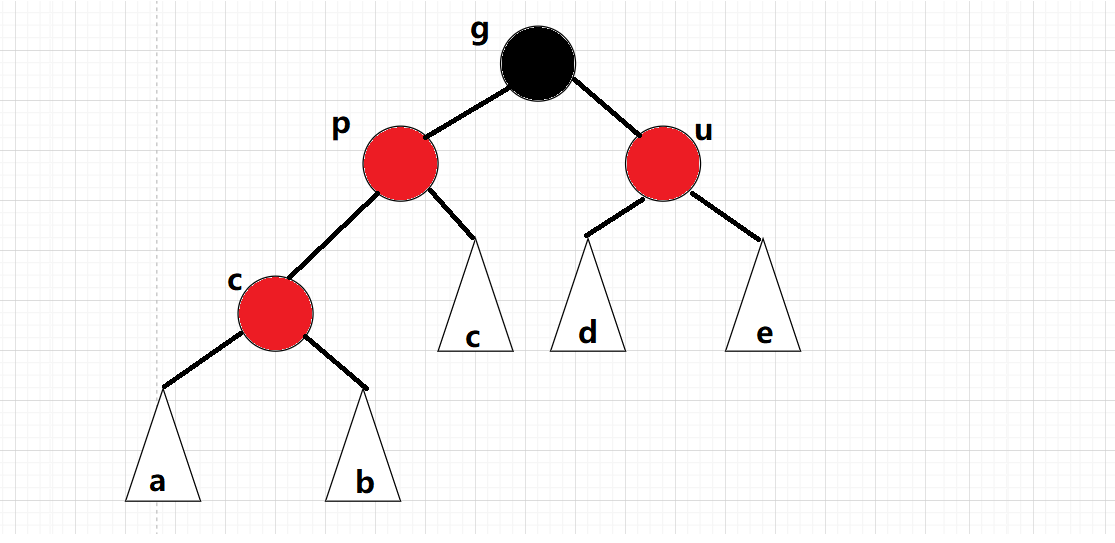
關鍵看u結點,根結點的顏色為黑色,不能有連續的紅色結點,所以上面的情況已經出現連續的紅色結點了,此時我們需要進行調整:
把p結點改為黑色,同時把u結點也改為黑色(符合性質四:每條路徑上的黑色節點數量相同),最后在把g結點改為紅色;如果g是子樹的話,g一定會有雙親,為了維持每條路徑上黑色節點的數量,g必須變紅,不然會多出一個黑色節點,在把g結點當做cur結點繼續往上調整,當g為根結點時,在把g置為黑色:
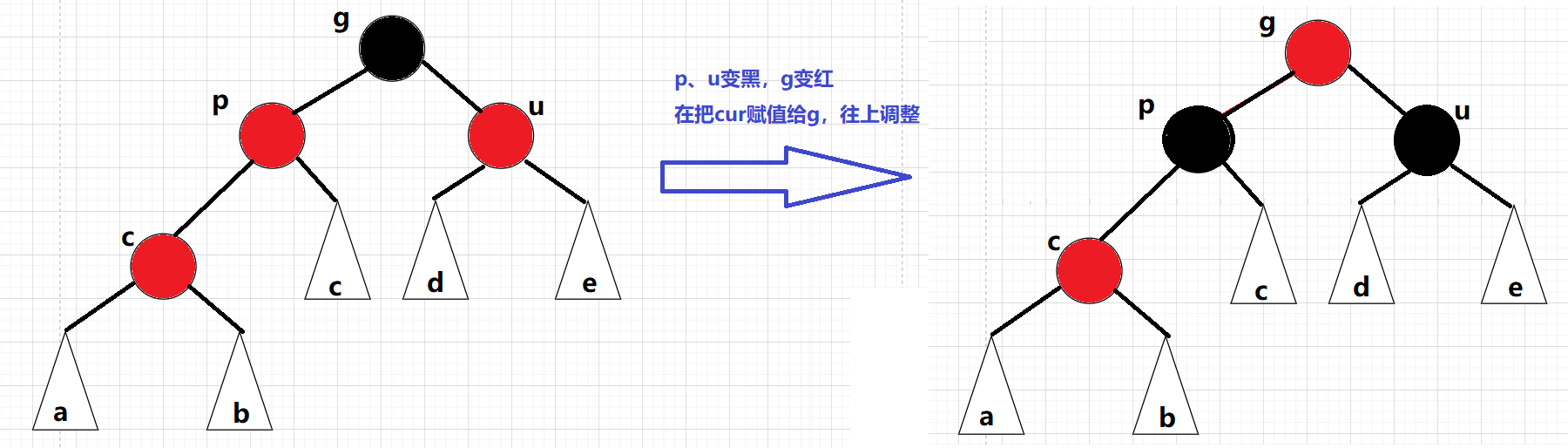
代碼實現:
while (parent && parent->_col == RED)
{
Node* grandfater = parent->_parent;
if (parent == grandfater->_left)
{
Node* uncle = grandfater->_right;
//情況一:u存在且為紅
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfater->_col = RED;
cur = grandfater;
parent = cur->_parent;
}
else//其他情況
{
}
}
else//parent==grandfater->_right
{
Node* uncle = grandfater->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfater->_col = RED;
cur = grandfater;
parent = cur->_parent;
}
else
{
}
}
}
_root->_col = BLACK;情況二:cur為紅,p為紅,g為黑,u不存在/u為黑,gpc在同一側:
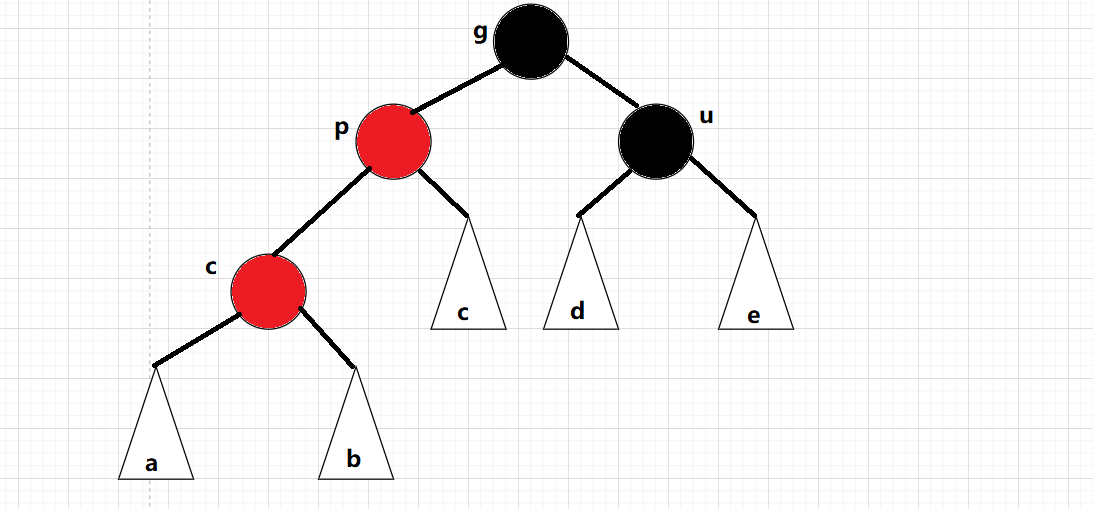
此時u的情況:
如果u結點不存在,則cur一定是新增結點,因為如果cur不是新增結點:則cur和p一定有一個節點時黑色,就不滿足每條路徑都有相同的黑色結點的性質。
如果u結點存在,則其一定是黑色的,那么c節點原來的顏色一定是黑色,在其子樹調整過程中變為了紅色
如果p為g的左孩子,cur為p的左孩子,則進行右單旋轉;
如果p為g的右孩子,cur為p的右孩子,則進行左單旋轉,
同時,p、g變色–p變黑,g變紅
以下情況:u不存在,cur為新增節點,進行右單旋:
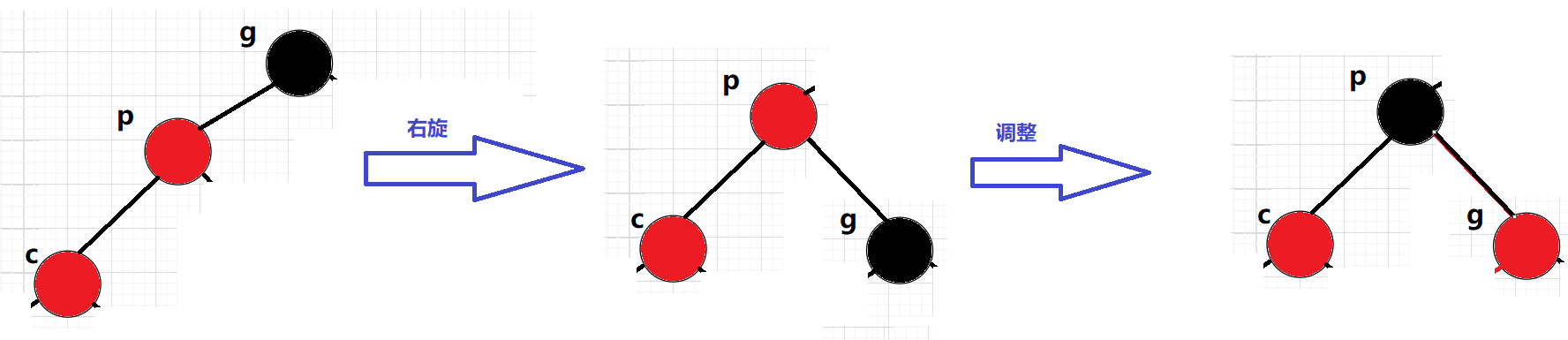
以下情況:u結點存在且為黑:
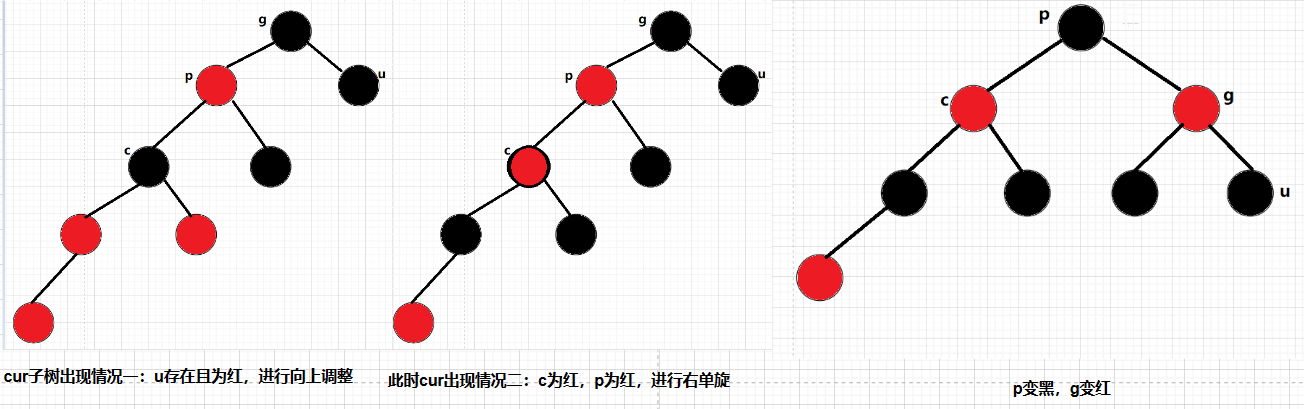
情況三: cur為紅,p為紅,g為黑,u不存在/u為黑,gpc不在同一側:
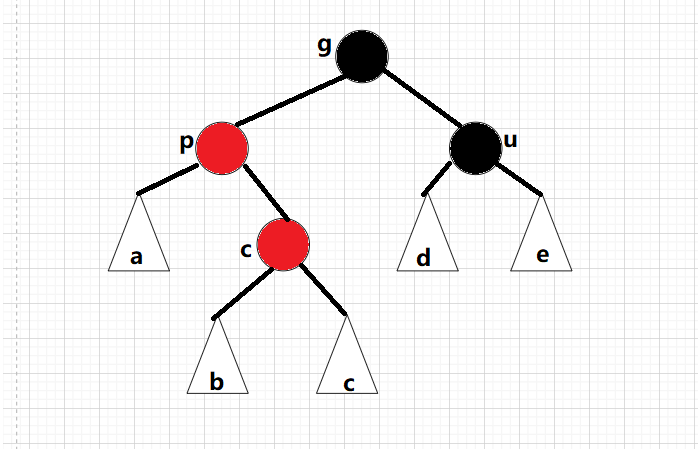
這時候我們就需要進行雙旋了:
p為g的左孩子,cur為p的右孩子,對p做左單旋轉;
p為g的右孩子,cur為p的左孩子,對p做右單旋轉; 旋轉之后則轉換成了情況2,在繼續進行調整即可
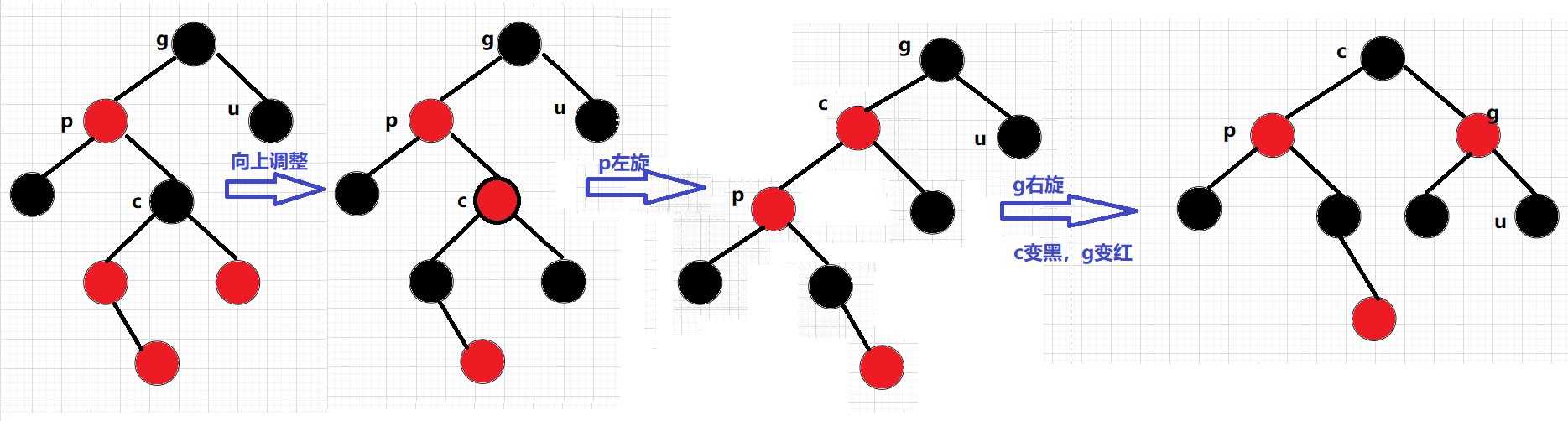
送上源碼:
#pragma once
#include <iostream>
#include <assert.h>
#include <time.h>
using namespace std;
enum Color
{
RED,
BLACK,
};
template<class K, class V >
struct RBTreeNode
{
pair<K, V> _kv;
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Color _col;
RBTreeNode(const pair<K,V>& kv)
:_kv(kv)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_col(RED)
{}
};
template<class K,class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_col = RED;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
while (parent && parent->_col == RED)
{
Node* grandfater = parent->_parent;
if (parent == grandfater->_left)
{
Node* uncle = grandfater->_right;
//情況一:u存在且為紅
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfater->_col = RED;
//向上調整
cur = grandfater;
parent = cur->_parent;
}
else
{
//情況2
if (cur == parent->_left)
{
RotateR(grandfater);
parent->_col = BLACK;
grandfater->_col = RED;
}
//情況3
else
{
// g
// p
// c
RotateL(parent);
RotateR(grandfater);
cur->_col = BLACK;
grandfater->_col = RED;
}
break;
}
}
else//parent==grandfater->_right
{
Node* uncle = grandfater->_left;
//情況1:u存在且為紅色
if (uncle && uncle->_col == RED)
{
uncle->_col = parent->_col = BLACK;
grandfater->_col = RED;
//向上調整
cur = grandfater;
parent = cur->_parent;
}
else
{
//情況2:u不存在/u存在為黑色
//g
// p
// c
if (cur == parent->_right)
{
RotateL(grandfater);
grandfater->_col = RED;
parent->_col = BLACK;
}
//情況3
// g
// p
// c
else
{
RotateR(parent);
RotateL(grandfater);
cur->_col = BLACK;
grandfater->_col = RED;
}
break;
}
}
}
//根變黑
_root->_col = BLACK;
return true;
}
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ppNode == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
subLR->_parent = parent;
Node* ppNode = parent->_parent;
parent->_parent = subL;
subL->_right = parent;
if (ppNode == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
void InOrder()
{
_InOrder(_root);
}
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
bool Check(Node*root,int blackNum,int ref)
{
if (root == nullptr)
{
//cout << blackNum << endl;
if (blackNum != ref)
{
cout << "違反規則:本條路徑的黑色結點的數量根最左路徑不相等" << endl;
return false;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "違反規則:出現連續的紅色結點" << endl;
return false;
}
if (root->_col == BLACK)
{
++blackNum;
}
return Check(root->_left,blackNum,ref)
&& Check(root->_right,blackNum,ref);
}
bool IsBalance()
{
if (_root == nullptr)
{
return true;
}
if (_root->_col != BLACK)
{
return false;
}
int ref = 0;
Node* left = _root;
while (left)
{
if (left->_col == BLACK)
{
++ref;
}
left = left->_left;
}
return Check(_root,0,ref);
}
private:
Node* _root = nullptr;
};
void TestRBTree1()
{
//int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
RBTree<int, int> t;
for (auto e : a)
{
t.Insert(make_pair(e, e));
}
t.InOrder();
cout << t.IsBalance() << endl;
}
void TestRBTree2()
{
srand(time(0));
const size_t N = 100000;
RBTree<int, int> t;
for (size_t i = 0; i < N; i++)
{
size_t x = rand();
t.Insert(make_pair(x, x));
}
cout << t.IsBalance() << endl;
}感謝各位的閱讀,以上就是“C++ RBTree紅黑樹的性質與實現方法是什么”的內容了,經過本文的學習后,相信大家對C++ RBTree紅黑樹的性質與實現方法是什么這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。