您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“Java數據結構之KMP算法怎么實現”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“Java數據結構之KMP算法怎么實現”吧!
這是最常見的算法字符串匹配算法,暴力匹配也叫樸素匹配。
思路很簡單,從主串的第i個字符開始遍歷,依次與子串的每個字符進行匹配,如果某個字符匹配失敗,則主串回溯第i+1個字符,子串回溯到第1個字符,重新開始匹配,直到遍歷完主串匹配失敗或者遍歷完子串匹配成功。
很明顯這種算法需要在一個雙重for循環中實現,時間復雜度為O(m*n),m為主串長度,n為子串長度。隨著字符串長度的增長,時間復雜度快速上升。
Java中字符串的contains方法實際上就是采用的BF算法。
public static int bf(String word, String k) {
char[] wordChars = word.toCharArray();
char[] keyChars = k.toCharArray();
for (int i = 0; i < wordChars.length; i++) {
int j = 0, x = i;
//依次匹配
while (x < wordChars.length && j < keyChars.length && wordChars[x] == keyChars[j]) {
x++;
j++;
}
if (j == keyChars.length) {
return i;
}
}
return -1;
}KMP 算法是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 于1977年共同提出的,稱之為 Knuth-Morria-Pratt 算法,簡稱 KMP 算法。
KMP算法是一種改進的字符串匹配算法,核心是利用之前的匹配失敗時留下的信息,選擇最長匹配長度直接滑動,從而減少匹配次數。KMP 算法時間復雜度為O(m+n),m為主串長度,n為子串長度。
BF匹配失敗之后,主串和子串都會最大回溯,但是很多時候都是沒有必要的。例如對于主串abababcd,子串ababc,第一次匹配之后,很明顯主串和子串會匹配失敗,但是我們能夠知道他們的能夠匹配的前綴串,即abab:
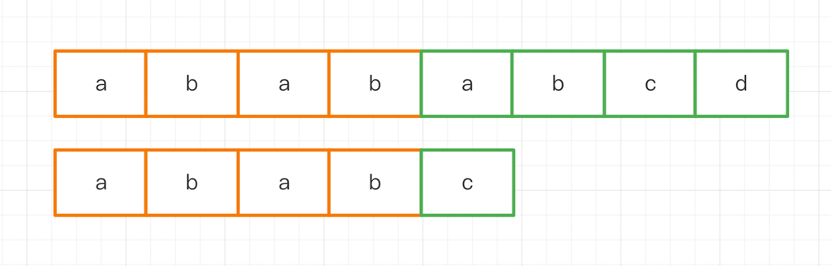
如果在第二次匹配的時候,主串不回溯,子串滑動兩個字符長度,那么我們就能在第二次的時候實現匹配成功。
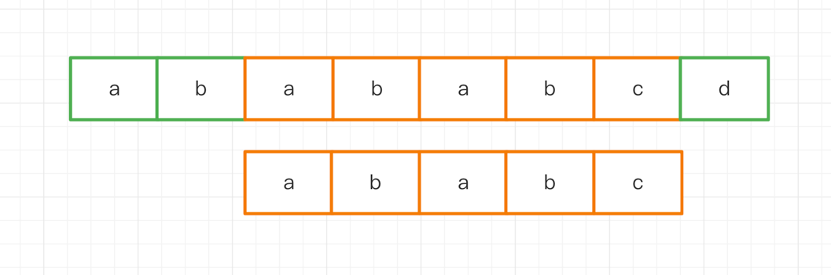
到這里,這種加速的方法已經呼之欲出了,但是我們先介紹兩個重要概念:
1.匹配前綴:在某一次主串和子串的匹配失敗之后,前面匹配成功的那部分子串就被稱為匹配前綴。這就是一次匹配失敗時留下的信息。
例如主串abcde,子串abcc,那么在第一次匹配的時候,匹配前綴為abc。
2.最長匹配長度:對于每次匹配失敗后的匹配前綴串,其前綴子串(連續,且一定包括第一個字符,不包括最后一個字符)和后綴子串(連續,且一定包括最后一個字符,不包括第一個字符)中,相同的前后綴子串的最長子串長度,此時的前綴、后綴字串也被稱為最長真前綴、后綴子串。
例如匹配前綴abc,沒有匹配的前綴和后綴,那么其最長匹配長度為0。
例如匹配前綴cbcbc,最長匹配的前綴和后綴子串為cbc,那么其最長匹配長度為3。
例如匹配前綴abbcbab,最長匹配的前綴和后綴子串為ab,那么其最長匹配長度為2。
有了這兩個概念,那么我們才能進行跳躍式滑動,對于主串,在匹配失敗的位置不進行回溯,對于子串,則是回溯(滑動)到其匹配前綴的最長匹配長度的位置上繼續匹配,這樣就跳過了之前的部字符串的匹配,且只需要匹配剩下的部分字符串即可。
我們再詳細解釋下,這里子串跳過的到底什么?實際上它跳過的就是匹配前綴串的最長匹配長度串。
設主串abababcd,子串ababc,第一次匹配失敗之后,主串匹配索引i=4,子串匹配索引j=4,此時匹配的相同前綴串為abab,它的最長匹配長度為2,即最長前綴串ab和最長后綴串ab。
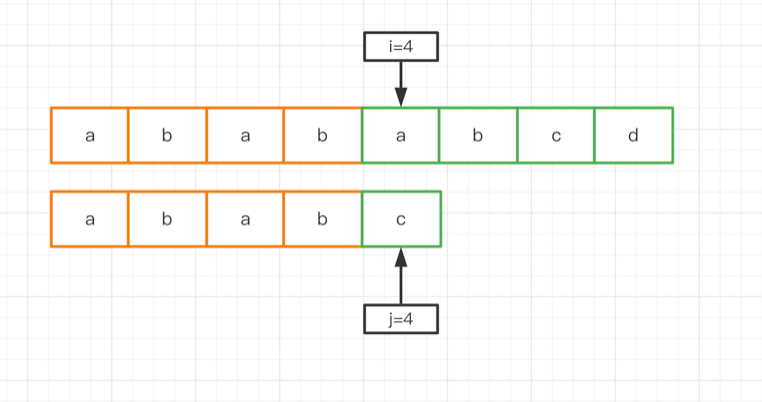
那么第二次匹配之前,字串匹配索引j直接跳到第一匹配的相同前綴串的最長匹配長度的索引位置上即j=2。我們可以這么理解,主串的第一次匹配的相同前綴串的最長匹配后綴,與子串第一次匹配的相同前綴串的最長匹配前綴相等(或者說重合)。這是我們在底層一次失敗匹配之后得到的有效信息,在第二次匹配時自然可以利用起來,利用最長的前后綴匹配信息,跳過這些多余的匹配,實現加速。(后續學習的AC自動機也是采用了前后綴匹配的思想)
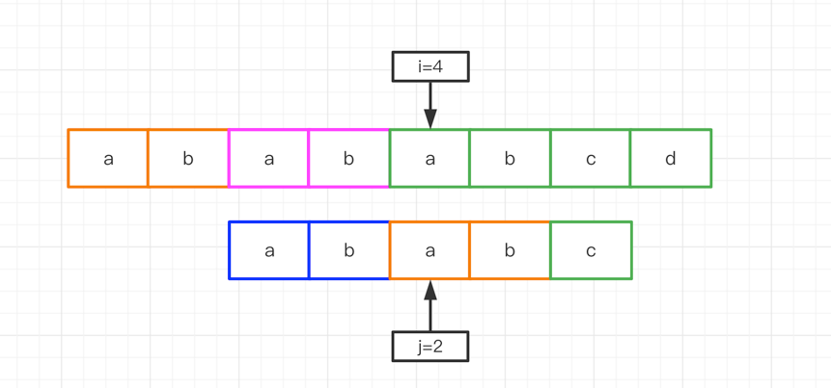
這就是KMP算法加速的核心原理,每次匹配失敗之后,利用匹配失敗的信息,找到最長匹配長度,然后主串不回溯,子串盡可能少的回溯,相比于BF算法,減少了沒必要的匹配次數。
基于上面的原理,我們知道可能會不止一次查找最長匹配長度,而且我們會發現,最長匹配長度的范圍只能在子串長度范圍之內,而且其計算結果只和子串有關。那么我們就可以先初始化一個數組,用來保存不同長度的前綴的最長匹配長度。
這就是所謂的next數組,也被稱為部分匹配表(Partial Match Table),也是KMP算法的核心。next數組的大小就是子串的長度,每個的索引位置i表示長度為i+1的子串的匹配前綴子串,值v表示對應匹配前綴子串的最長匹配長度。
假設子串為ababc,那么next數組值為:
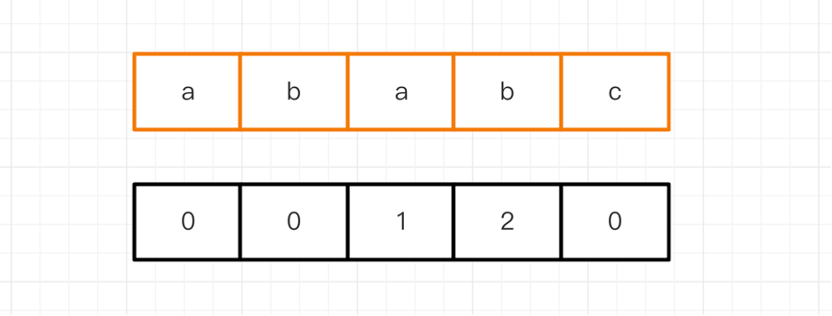
假設子串為abcabdabcabc,那么對應的next數組如下:

其實很好理解:
| 子串匹配前綴串 | 最長匹配長度 |
|---|---|
| a | 0 |
| ab | 0 |
| abc | 0 |
| abca | 1 |
| abcab | 2 |
| abcabd | 0 |
| abcabda | 1 |
| abcabdab | 2 |
| abcabdabc | 3 |
| abcabdabca | 4 |
| abcabdabcab | 5 |
| abcabdabcabc | 3 |
現在,我們的首要問題變成了求next數組。
首先,切next數組的問題實際上就是求最大的前、后綴長度的問題,那么我們可以使用最樸素的方式求解:
public static int[] getNext(String word) {
int[] next = new int[word.length()];
//從兩個字符的子串開始遍歷
for (int i = 1; i < word.length(); i++) {
int k = i;
//從最大的最長匹配值開始縮短
while (k > 0) {
//如果前綴等于后綴,那么表示獲取到了最長匹配,直接返回
if (word.substring(0, k).equals(word.substring(i - (k - 1), i + 1))) {
next[i] = k;
break;
}
k--;
}
}
return next;
}不難發現,求解next數組的時間復雜度為O(n^2),是否有更快速的方法呢?當然有,可以發現,在求next[i]的最長匹配長度的時候,next[0], next[1], … next[i-1]的結果已經求出來了。因此我們嘗試利用此前的結果直接推導出后面的結果。下面是分情況討論。
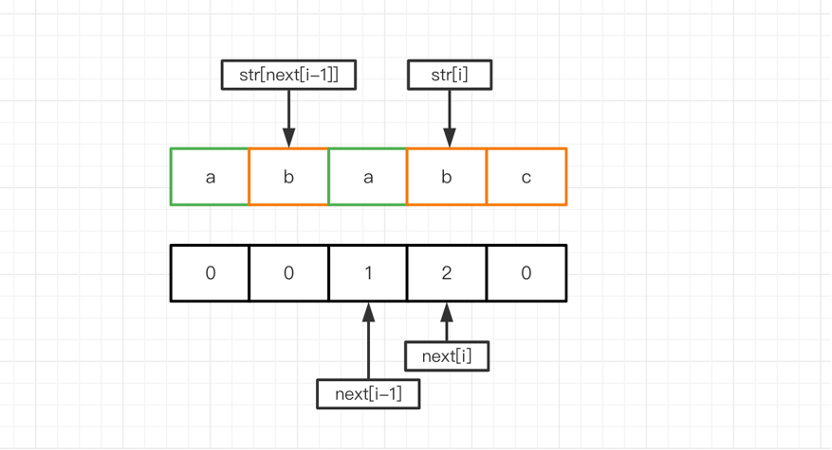
設子串為str=ababc,i=3,那么next[i-1]=1,即子串aba的的最長匹配長度為1,那么str[next[i-1]]實際上就是最長匹配子串前綴后一個字符,即str[1]=b。
如果str[i]=str[next[i-1]],就相當于在前一個子串的最長匹配長度的基礎上增加了一位,即next[i]=next[i-1]+1。如下圖:
如果str[i]!=str[next[i-1]],此時就會復雜一些。此時我們需要縮短最長匹配子串的長度,具體怎么縮短呢?
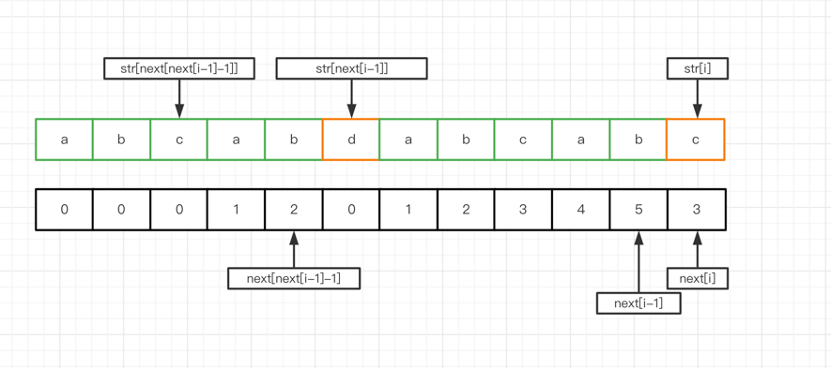
設str = abcabdabcabc,設i = 11,即最后一個字符c,那么next[i-1] = 5,但是由于str[i] != str[next[i-1]],即d != c,那么此時我們需要求i-1的最長匹配長度子串abcab的最長匹配長度子串,即next[next[i-1]-1] = 2,然后判斷str[i]是否等于str[next[next[i-1]-1]],如果相等則同第一種情況,否則繼續縮減直到next[next[i-1]-1]為0為止,此時表示當前子串的最長匹配長度也為0。如下圖:
基于上面的規律,我們的改進算法如下:
public static int[] getNext2(String k) {
int[] next = new int[k.length()];
char[] chars = k.toCharArray();
//i表示匹配的字符索引,pre表示前一個子串的最長匹配長度,即next[i-1]
int i = 1, pre = next[i - 1];
while (i < k.length()) {
//如果新增的字符與前一個子串的最長匹配子串前綴的后一個字符相等
if (chars[i] == chars[pre]) {
//next[i]=next[i-1]+1
pre++;
next[i] = pre;
//繼續后移
i++;
}
//如果不相等,且前一個子串的最長匹配長度不為0
//那么求i-1的最長匹配長度子串的最長匹配長度子串,即pre=next[next[i-1]-1]
//然后在下一輪循環中繼續比較chars[i] == chars[pre],此時i并沒有自增
else if (pre != 0) {
//next[next[i-1]-1]
pre = next[pre - 1];
}
//如果不相等,且前一個子串的最長匹配長度為0,那么說明當前子串的最長匹配長度也為0
else {
//當前子串的最長匹配長度為0
next[i] = 0;
//繼續后移
i++;
}
}
return next;這種算法的時間復雜度為O(n),大大縮短了求next數組的時間。
有了next數組,那么KMP算法就很容易實現了。
使用i和j分別表示主串和子串的匹配進度,i永遠不會回退,依次匹配主串和子串的字符:
1.如果字符相等則推進i、j,并且判斷如果匹配到了一個完整的子串,那么返回起始索引。
2.如果不相等:
如果當前子串進度為0,那么子串不需要回退,主串向后推進i,重新開始匹配;
如果當前子串進度不為0,那么子串進度需要回退到next[j-1]的位置,此前的位置不再需要匹配,主串不需要向后推進i,隨后重新開始匹配。
如果i進度匹配完畢,那么退出循環,表示沒有匹配到任何完整的子串,返回-1。
public static int kmp(String word, String k) {
int[] next = getNext(k);
//i,j分別表示主串和子串的匹配進度
int m = word.length(), n = k.length(), i = 0, j = 0;
//如果i匹配完畢,那么退出循環
while (i < m) {
//如果字符相等,那么向后推進i、j
if (word.charAt(i) == k.charAt(j)) {
i++;
j++;
//如果匹配到了一個完整的子串
if (j == n) {
//返回起始索引
return i - n;
}
}
//如果當前子串進度為0,那么子串不需要回退,主串向后推進i
else if (j == 0) {
i++;
}
//如果當前子串進度不為0,那么子串需要回退,主串不需要向后推進i
else {
//子串進度j回退
j = next[j - 1];
}
}
return -1;
}上面我們的實現是返回第一個匹配到的模式串的起始索引,那么如果我們需要返回所有匹配到的模式串的起始索引呢?
其實也很簡單。在每次匹配某個字符成功之后判斷,如果匹配到了一個完整的子串,那么我們求起始索引并且加入結果集,然后子串點位j需要回退,繼續循環。
public static List<Integer> kmpAll(String word, String k) {
List<Integer> res = new ArrayList<>();
int[] next = getNext(k);
//i,j分別表示主串和子串的匹配進度
int m = word.length(), n = k.length(), i = 0, j = 0;
//如果i匹配完畢,或者j匹配完畢,那么退出循環
while (i < m) {
//如果字符相等,那么向后推進i、j
if (word.charAt(i) == k.charAt(j)) {
i++;
j++;
//如果匹配到了一個完整的子串
if (j == n) {
//將起始索引加入結果集
res.add(i - n);
//子串進度j回退
j = next[j - 1];
}
}
//如果當前子串進度為0,那么子串不需要回退,主串向后推進i
else if (j == 0) {
i++;
}
//如果當前子串進度不為0,那么子串需要回退,主串不需要向后推進i
else {
//子串進度j回退
j = next[j - 1];
}
}
return res;
}感謝各位的閱讀,以上就是“Java數據結構之KMP算法怎么實現”的內容了,經過本文的學習后,相信大家對Java數據結構之KMP算法怎么實現這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。