您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文小編為大家詳細介紹“怎么用Python遺傳算法處理TSP問題”,內容詳細,步驟清晰,細節處理妥當,希望這篇“怎么用Python遺傳算法處理TSP問題”文章能幫助大家解決疑惑,下面跟著小編的思路慢慢深入,一起來學習新知識吧。
那么在開始之前的話,咱們來仔細描述一下這個TSP問題。這個打過數模,或者接觸過智能優化或者機器學習方面的朋友應該都知道,當然為了本文的受眾普適性,咱們在這里盡可能去完善一點,說清楚,這樣便于咱們去實際解決問題。
那么這個問題的其實簡單,是這樣子的:
在我們的N維平面是,咱們今天的話是拿這個二維平面來的,在這個平面上有很多個城市,城市之間是彼此聯通的,我們現在要找出一條最短的路徑可以將全部城市都走完。例如我們有城市A,B,C,D,E。現在知道了城市間的坐標,也就是相當于知道了城市之間的距離,那么現在找到一個順序,能夠使得走完A,B,C,D,E所有城市的路徑和最短。比如計算完之后可能是B-->A-->C-->E-->D。換一句話說找到這個順序。
首先要解決這個問題的話,其實方案有很多,說變白了,咱們就是要找到一個順序,能夠讓路徑之和最小,那么最容易想到的自然就是枚舉,例如讓A先走然后看距離A最近的假設是B,那么就走B,然后從B走。當然這個是局部貪心策略,很容易走到局部最優,那么這個時候我們可以考慮DP,也就是說依然假設從A開始,然后確保2個城市最短,3個城市最短,4個5個。最后在假設從B開始同理。或者直接 枚舉全部情況,計算距離。但是無論如何,隨著城市數量的上升,他們的復雜度都會增加,所以這個時候我們就要想辦法讓計算能不能發揮一下咱們人類的專長了。我稱之為“瞎蒙”。
現在我們來聊聊這個智能算法,以及為什么要用著玩意,剛剛咱們說了前面的方案對于大量的數據計算量會很大,也不見得編寫簡單。那么這個時候,首先單單對于TSP問題來說,我們要的就是一個序列,一個不會重復的序列。那么這個時候,有什么一個更加簡便的方案,而且在數據足夠大的情況下,我們也不見得需要一個完全精準,完全最小的解,只要接近就好。那么這個時候,采用傳統的那些算法的話,一就是一,他只會按照我們的規則去計算,而且我們也確實不知道標準答案是什么,對傳統算法也比較難去設定一個閾值去停止運算。但是對我們人來說,有一種東西叫做“運氣”,有的人運氣賊好,可能一發入魂,一下子就懵出了答案。那么我們的智能算法其實就是有點類似于“蒙”。但是人家蒙是講究技巧的,例如經驗告訴我們,三長一短選最短,通過這個技巧可以去蒙一下答案,或者找男盆友的時候像博主一樣帥氣的男孩紙,只要一張40系(30也可以)顯卡就可以輕松帶走一樣。蒙是要技巧的,我們管這個叫做策略。
那么我們剛剛說的這個技巧,這個蒙的技巧。在智能算法里面,這個蒙,就是我們的一種策略。我們要怎么去蒙才能夠讓我們的解更加合理。那么這個時候,就開始百花齊放了,這里我就不念經了,我們拿最金典的兩個算法為例子,一個是遺傳算法,一個是粒子群算法(PSO)。為例子,他們就是采用了一種策略去蒙,例如遺傳算法,通過模擬物競天擇,一開始先隨機蒙出一堆解,一堆序列,然后按照咱們的這個物競天擇的策略出篩選這些解,然后通過這些解再去蒙出新的更好的解。如此往復,之后蒙出不錯的解。粒子群也是類似的,這些部分咱們用的時候再詳細說明。
現在咱們已經知道了這個策略,那么算法是啥,其實就是實現這些策略的步驟啊,就是咱們的代碼,咱們的循環,數據結構。我們要去實現剛剛說的例如物競天擇,例如咱們TSP,如何隨機生成一堆解。
ok,到這里咱們已經說完了,基本的一些概念,那么這個時候的話,咱們來看看咱們如何表示這個TSP的問題,這個其實很簡單,咱們這邊的話就簡單的準備一個測試數據,我們這里假設有14個城市,那么我們的這些城市的數據如下:
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54, 22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02, 17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38, 21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
我們后面都用這組數據進行測試,現在在上面已經有了14個城市。
那么接下來我們開始我們的解決方案
ok,那么我們來說一說咱們的這個遺傳算法是怎么一回事,之后的話,咱們用這個來解決這個TSP問題。
那么現在的話,我們來看看我們的遺傳算法是怎么蒙的。
遺傳算法其實是在用計算機模擬我們的物種進化。其實更加通俗的說法是篩選,這個就和我們袁老爺爺種植水稻一樣。有些個體發育良好,有些個體發育不好,那么我就先篩選出發育好的,然后讓他們去繁衍后代,然后再篩選,最后得到高產水稻。其實也和我們社會一樣,不努力就木有女朋友就不能保留自己的基因,然后剩下的人就是那些優秀的人和富二代的基因,這就是現實呀。所以得好好學習,天天向上!
那么回到主題,我們的遺傳算法就是在模擬這一個過程,模擬一個物競天擇的過程。
所以在我們的算法里面也是分為幾大塊
首先我們的種群需要先繁殖。這樣才能不斷產生優良基于,那么對應我們的算法,假設我們需要求取
Y = np.sin(10 * x) * x + np.cos(2 * x) * x
的最大值(在一個范圍內)那么我們的個體就是一組(X1)的解。好的個體就會被保留,不好的就會被pass,選擇標準就是我們的函數 Y 。那么問題來了如何模擬這個過程?我們都知道在繁殖后代的時候我們是通過DNA來保留我們的基因信息,在這個過程當中,父母的DNA交互,并且在這個過程當中會產生變異,這樣一來,父母雙方的優秀基于會被保存,并且產生的變異有可能誕生更加優秀的后代。
所以接下來我們需要模擬我們的DNA,進行交叉和變異。
這個交叉過程和我們的生物其實很像,當然我們在我們的計算機里面對于數字我們可以將其轉化為二進制,當做我們的DNA
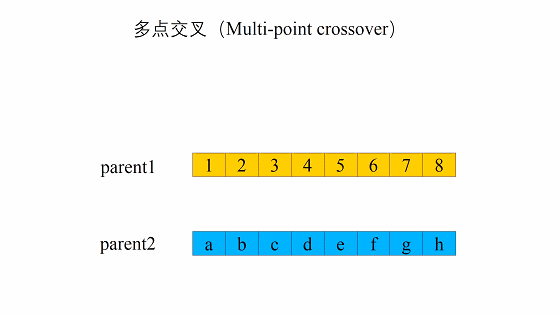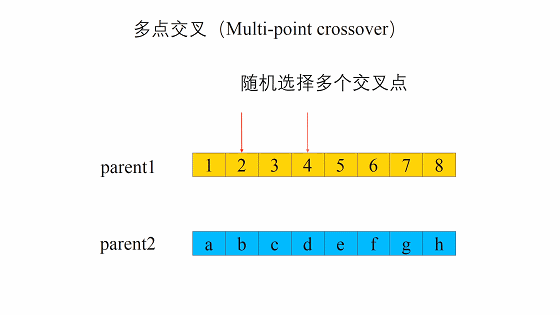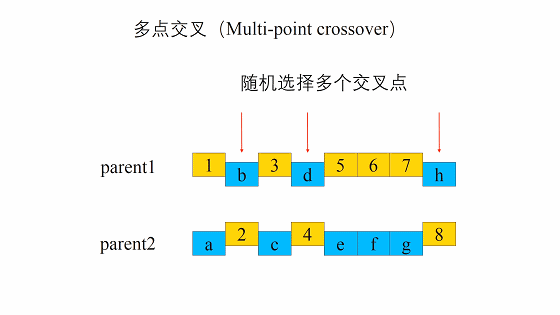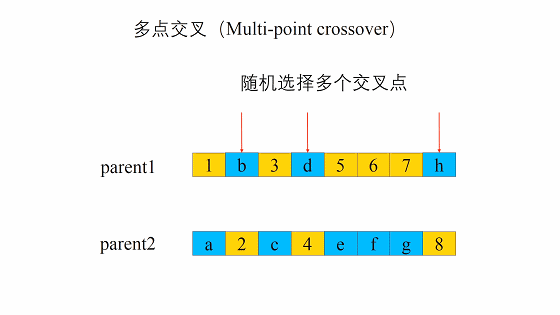
交叉的方式有很多,我們這邊選擇這一個,進行交叉。
那這個在我們這里就更加簡單了
我們只需要在交叉之后,再隨機選擇幾個位置進行改變值就可以了。當然變異的概率是很小的,并且是隨機的,這一點要注意。并且由于變異是隨機的,所以不排除生成比原來還更加糟糕的個體。
最后我們按照一定的規則去篩選這個些個體就可以了,然后淘汰原來的個體。那么在我們的計算機里面是使用了兩個東西,首先我們要把原來二進制的玩意,給轉化為我們原來的十進制然后帶入我們的函數運算,然后保存起來,之后再每一輪統一篩選一下就好了。
這個咋說呢,說好聽點叫逆轉,難聽點就算,對于一些新的生成的不好的解,我們是要舍棄的。
那么這部分用代碼描述的話就是這樣的:
import numpy as np
import matplotlib.pyplot as plt
Population_Size = 100
Iteration_Number = 200
Cross_Rate = 0.8
Mutation_Rate = 0.003
Dna_Size = 10
X_Range=[0,5]
def F(x):
'''
目標函數,需要被優化的函數
:param x:
:return:
'''
return np.sin(10 * x) * x + np.cos(2 * x) * x
def CrossOver(Parent,PopSpace):
'''
交叉DNA,我們直接在種群里面選擇一個交配
然后就生出孩子了
:param parent:
:param PopSpace:
:return:
'''
if(np.random.rand()) < Cross_Rate:
cross_place = np.random.randint(0, 2, size=Dna_Size).astype(np.bool)
cross_one = np.random.randint(0, Population_Size, size=1) #選擇一位男/女士交配
Parent[cross_place] = PopSpace[cross_one,cross_place]
return Parent
def Mutate(Child):
'''
變異
:param Child:
:return:
'''
for point in range(Dna_Size):
if np.random.rand() < Mutation_Rate:
Child[point] = 1 if Child[point] == 0 else 0
return Child
def TranslateDNA(PopSpace):
'''
把二進制轉化為十進制方便計算
:param PopSpace:
:return:
'''
return PopSpace.dot(2 ** np.arange(Dna_Size)[::-1]) / float(2 ** Dna_Size - 1) * X_Range[1]
def Fitness(pred):
'''
這個其實是對我們得到的F(x)進行換算,其實就是選擇的時候
的概率,我們需要處理負數,因為概率不能為負數呀
pred 這是一個二維矩陣
:param pred:
:return:
'''
return pred + 1e-3 - np.min(pred)
def Select(PopSpace,Fitness):
'''
選擇
:param PopSpace:
:param Fitness:
:return:
'''
'''
這里注意的是,我們先按照權重去選擇我們的優良個體,所以我們這里選擇的時候允許重復的元素出現
之后我們就可以去掉這些重復的元素,這樣才能實現保留良種去除劣種。100--》70(假設有30個重復)
如果不允許重復的話,那你相當于沒有篩選
'''
Better_Ones = np.random.choice(np.arange(Population_Size), size=Population_Size, replace=True,
p=Fitness / Fitness.sum())
# np.unique(Better_Ones) #這個是我后面加的
return PopSpace[Better_Ones]
if __name__ == '__main__':
PopSpace = np.random.randint(2, size=(Population_Size, Dna_Size)) # initialize the PopSpace DNA
plt.ion()
x = np.linspace(X_Range, 200)
# plt.plot(x, F(x))
plt.xticks([0,10])
plt.yticks([0,10])
for _ in range(Iteration_Number):
F_values = F(TranslateDNA(PopSpace))
# something about plotting
if 'sca' in globals():
sca.remove()
sca = plt.scatter(TranslateDNA(PopSpace), F_values, s=200, lw=0, c='red', alpha=0.5)
plt.pause(0.05)
# GA part (evolution)
fitness = Fitness(F_values)
print("Most fitted DNA: ", PopSpace[np.argmax(fitness)])
PopSpace = Select(PopSpace, fitness)
PopSpace_copy = PopSpace.copy()
for parent in PopSpace:
child = CrossOver(parent, PopSpace_copy)
child = Mutate(child)
parent[:] = child
plt.ioff()
plt.show()這個代碼是以前寫的,逆轉沒有寫上(下面的有)
ok,剛剛的例子是拿的解方程,也就是說是一個連續問題吧,當然那個連續處理的話并不是很好,只是一個演示。那么我們這個的話其實類似的。首先我們的DNA,是城市的路徑,也就是A-B-C-D等等,當然我們用下標表示城市。
首先我們確定了使用城市的序號作為我們的個體DNA,例如咱們種群大小為100,有ABCD四個城市,那么他就是這樣的,我們先隨機生成種群,長這個樣:
1 2 3 4
2 3 4 5
3 2 1 4
...
那個1,2,3,4是ABCD的序號。
這里面的話,值得一提的就是,由于暫定城市需要是不能重復的,且必須是完整的,所以如果像剛剛那樣進行交叉或者變異的話,那么實際上會出點問題,我們不允許出現重復,且必須完整,對于我們的DNA,也就是咱們瞎蒙的個體。
由于咱們每一步在代碼里面都有注釋,所以的話咱們在這里就不再進行復述了。
from math import floor
import numpy as np
import matplotlib.pyplot as plt
class Gena_TSP(object):
"""
使用遺傳算法解決TSP問題
"""
def __init__(self, data, maxgen=200,
size_pop=200, cross_prob=0.9,
pmuta_prob=0.01, select_prob=0.8
):
self.maxgen = maxgen # 最大迭代次數
self.size_pop = size_pop # 群體個數,(一次性瞎蒙多少個解)
self.cross_prob = cross_prob # 交叉概率
self.pmuta_prob = pmuta_prob # 變異概率
self.select_prob = select_prob # 選擇概率
self.data = data # 城市的坐標數據
self.num = len(data) # 有多少個城市,對應多少個坐標,對應染色體的長度(我們的解叫做染色體)
"""
計算城市的距離,我們用矩陣表示城市間的距離
"""
self.__matrix_distance = self.__matrix_dis()
self.select_num = int(self.size_pop * self.select_prob)
# 通過選擇概率確定子代的選擇個數
"""
初始化子代和父代種群,兩者相互交替
"""
self.parent = np.array([0] * self.size_pop * self.num).reshape(self.size_pop, self.num)
self.child = np.array([0] * self.select_num * self.num).reshape(self.select_num, self.num)
"""
負責計算每一個個體的(瞎蒙的解)最后需要多少距離
"""
self.fitness = np.zeros(self.size_pop)
self.best_fit = []
self.best_path = []
# 保存每一步的群體的最優路徑和距離
def __matrix_dis(self):
"""
計算14個城市的距離,將這些距離用矩陣存起來
:return:
"""
res = np.zeros((self.num, self.num))
for i in range(self.num):
for j in range(i + 1, self.num):
res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
res[j, i] = res[i, j]
return res
def rand_parent(self):
"""
初始化種群
:return:
"""
rand_ch = np.array(range(self.num))
for i in range(self.size_pop):
np.random.shuffle(rand_ch)
self.parent[i, :] = rand_ch
self.fitness[i] = self.comp_fit(rand_ch)
def comp_fit(self, one_path):
"""
計算,咱們這個路徑的長度,例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def out_path(self, one_path):
"""
輸出我們的路徑順序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.num):
res += str(one_path[i] + 1) + '-->'
res += str(one_path[0] + 1) + '\n'
print(res)
def Select(self):
"""
通過我們的這個計算的距離來計算出概率,也就是當前這些個體DNA也就瞎蒙的解
之后我們在通過概率去選擇個體,放到child里面
:return:
"""
fit = 1. / (self.fitness) # 適應度函數
cumsum_fit = np.cumsum(fit)
pick = cumsum_fit[-1] / self.select_num * (np.random.rand() + np.array(range(self.select_num)))
i, j = 0, 0
index = []
while i < self.size_pop and j < self.select_num:
if cumsum_fit[i] >= pick[j]:
index.append(i)
j += 1
else:
i += 1
self.child = self.parent[index, :]
def Cross(self):
"""
模仿DNA交叉嘛,就是交換兩個瞎蒙的解的部分的解例如
A-B-C-D
C-D-A-B
我們選幾個交叉例如這樣
A-D-C-B
1,3號交換了位置,當然這里注意可不能重復啊
:return:
"""
if self.select_num % 2 == 0:
num = range(0, self.select_num, 2)
else:
num = range(0, self.select_num - 1, 2)
for i in num:
if self.cross_prob >= np.random.rand():
self.child[i, :], self.child[i + 1, :] = self.intercross(self.child[i, :],
self.child[i + 1, :])
def intercross(self, ind_a, ind_b):
"""
這個是我們兩兩交叉的具體實現
:param ind_a:
:param ind_b:
:return:
"""
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
ind_a1 = ind_a.copy()
ind_b1 = ind_b.copy()
for i in range(left, right + 1):
ind_a2 = ind_a.copy()
ind_b2 = ind_b.copy()
ind_a[i] = ind_b1[i]
ind_b[i] = ind_a1[i]
x = np.argwhere(ind_a == ind_a[i])
y = np.argwhere(ind_b == ind_b[i])
if len(x) == 2:
ind_a[x[x != i]] = ind_a2[i]
if len(y) == 2:
ind_b[y[y != i]] = ind_b2[i]
return ind_a, ind_b
def Mutation(self):
"""
之后是變異模塊,這個就是按照某個概率,去替換瞎蒙的解里面的其中幾個元素。
:return:
"""
for i in range(self.select_num):
if np.random.rand() <= self.cross_prob:
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
self.child[i, [r1, r2]] = self.child[i, [r2, r1]]
def Reverse(self):
"""
近化逆轉,就是說下一次瞎蒙的解如果沒有更好的話就不進入下一代,同時也是隨機選擇一個部分的
我們不是一次性全部替換
:return:
"""
for i in range(self.select_num):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
sel = self.child[i, :].copy()
sel[left:right + 1] = self.child[i, left:right + 1][::-1]
if self.comp_fit(sel) < self.comp_fit(self.child[i, :]):
self.child[i, :] = sel
def Born(self):
"""
替換,子代變成新的父代
:return:
"""
index = np.argsort(self.fitness)[::-1]
self.parent[index[:self.select_num], :] = self.child
def main(data):
Path_short = Gena_TSP(data) # 根據位置坐標,生成一個遺傳算法類
Path_short.rand_parent() # 初始化父類
## 繪制初始化的路徑圖
fig, ax = plt.subplots()
x = data[:, 0]
y = data[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(data) + 1)):
ax.annotate(txt, (x[i], y[i]))
res0 = Path_short.parent[0]
x0 = x[res0]
y0 = y[res0]
for i in range(len(data) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
print('初始染色體的路程: ' + str(Path_short.fitness[0]))
# 循環迭代遺傳過程
for i in range(Path_short.maxgen):
Path_short.Select() # 選擇子代
Path_short.Cross() # 交叉
Path_short.Mutation() # 變異
Path_short.Reverse() # 進化逆轉
Path_short.Born() # 子代插入
# 重新計算新群體的距離值
for j in range(Path_short.size_pop):
Path_short.fitness[j] = Path_short.comp_fit(Path_short.parent[j, :])
index = Path_short.fitness.argmin()
if (i + 1) % 50 == 0:
print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[index]))
print('第' + str(i + 1) + '步后的最優路徑:')
Path_short.out_path(Path_short.parent[index, :]) # 顯示每一步的最優路徑
# 存儲每一步的最優路徑及距離
Path_short.best_fit.append(Path_short.fitness[index])
Path_short.best_path.append(Path_short.parent[index, :])
return Path_short # 返回遺傳算法結果類
if __name__ == '__main__':
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
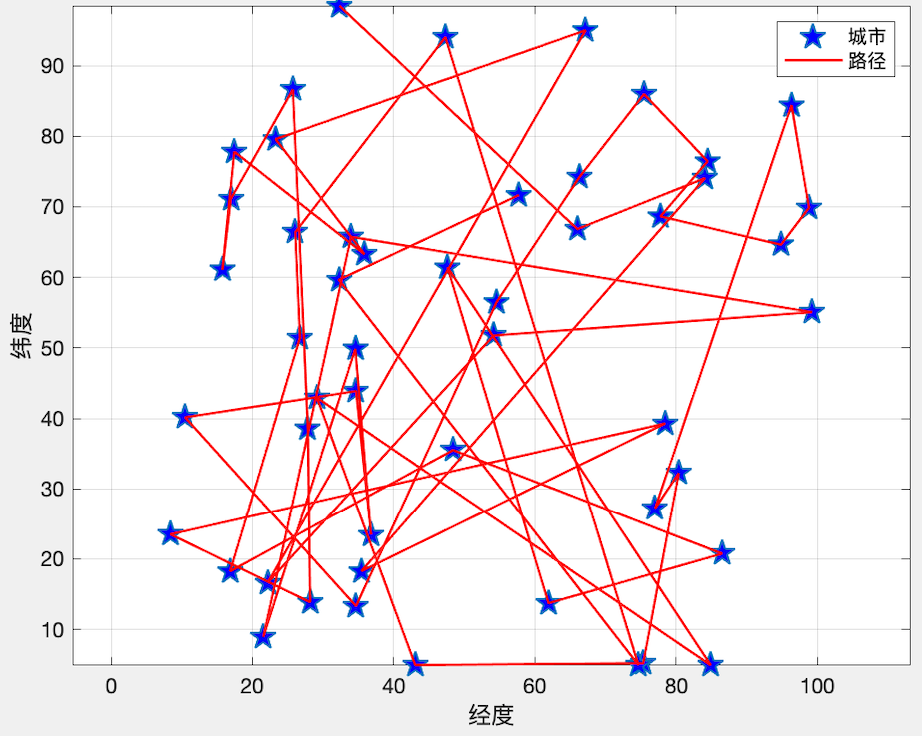
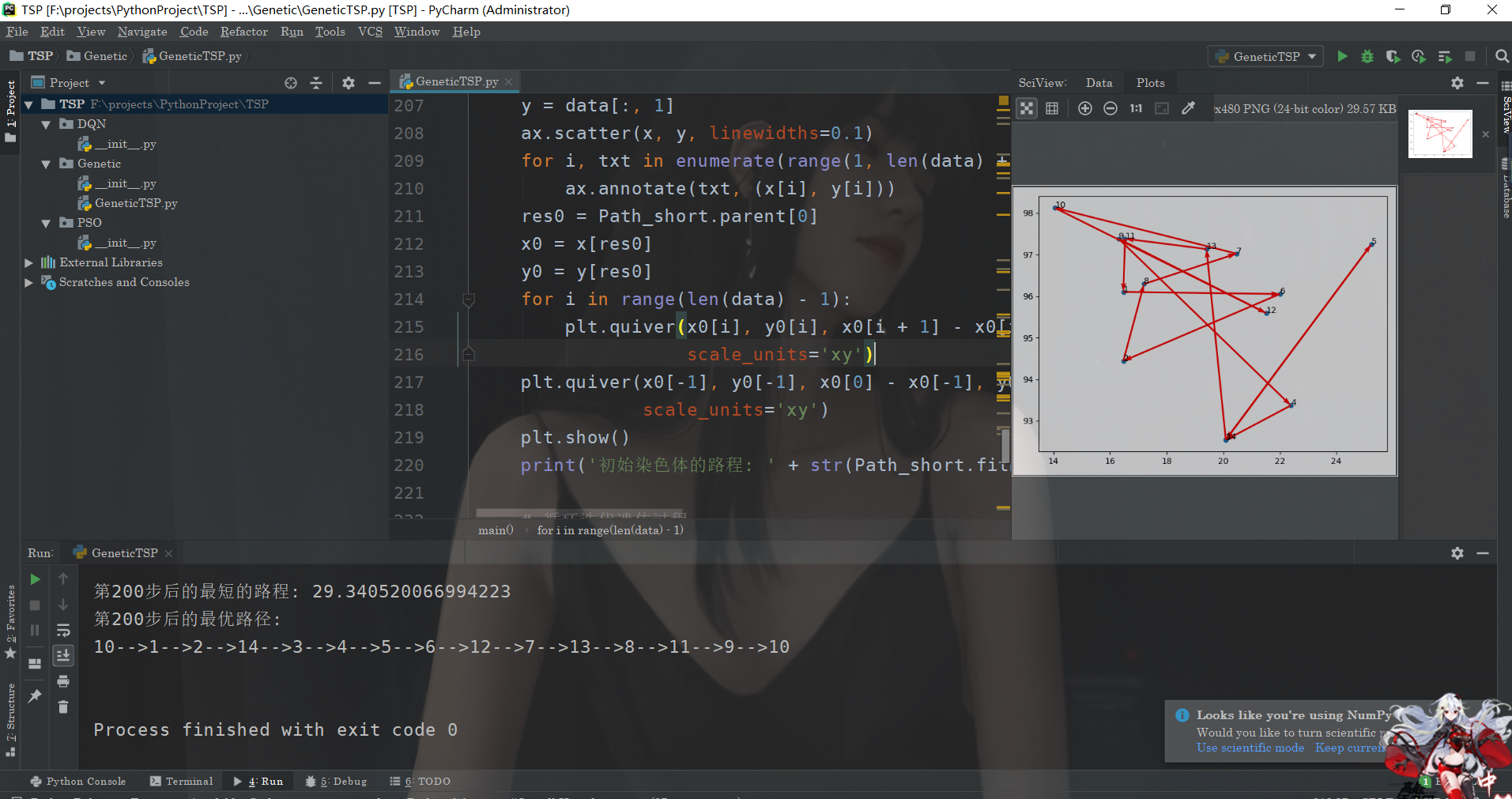
main(data)ok,我們來看看運行的結果:
讀到這里,這篇“怎么用Python遺傳算法處理TSP問題”文章已經介紹完畢,想要掌握這篇文章的知識點還需要大家自己動手實踐使用過才能領會,如果想了解更多相關內容的文章,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。