您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了怎么使用Python PSO算法處理TSP問題的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇怎么使用Python PSO算法處理TSP問題文章都會有所收獲,下面我們一起來看看吧。
那么開始之前,我們還是來聊聊基本的PSO算法。核心就一個:
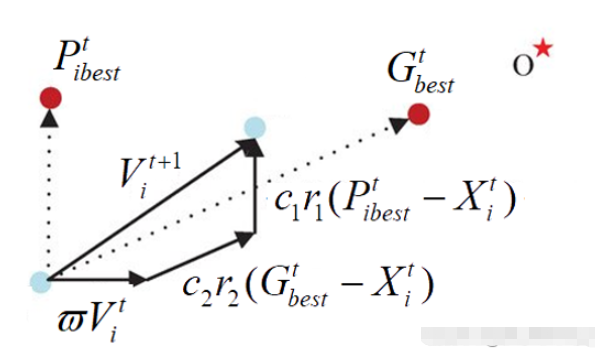
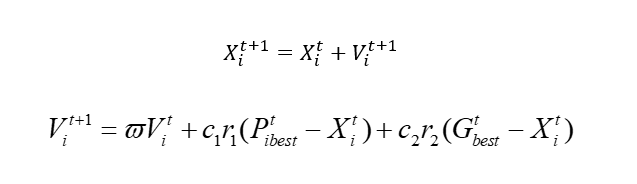
來我們來解釋一下這個公式,你就懂了。
老規矩我們假設有一個方程 y=sin(x1)+cos(x2)
PSO算法通過模擬鳥類遷移來實現咱們的優化,這個怎么來的,就不說了,就說說這個核心。
我們剛剛的方程當中,有兩個變量,x1,x2。由于是模擬鳥兒,所有為了實現瞎蒙大法,這里引入了速度的概念,x自然就是咱們的可行域,也就是解的空間。通過改變速度,來讓x進行移動,也就是改變x的值。其中Pbest,表示這個鳥自己走過的位置里面最優的解,Gbest表示整個種群的最優解。什么意思,也就是說隨著移動,這個鳥可能會走到更差的位置,因為和遺傳不一樣,他是不好的就干掉了,而這個不會。當然這里面涉及到很多局部問題,咱們這里都不討論,沒有哪一個算法是完美的,這個就對了。
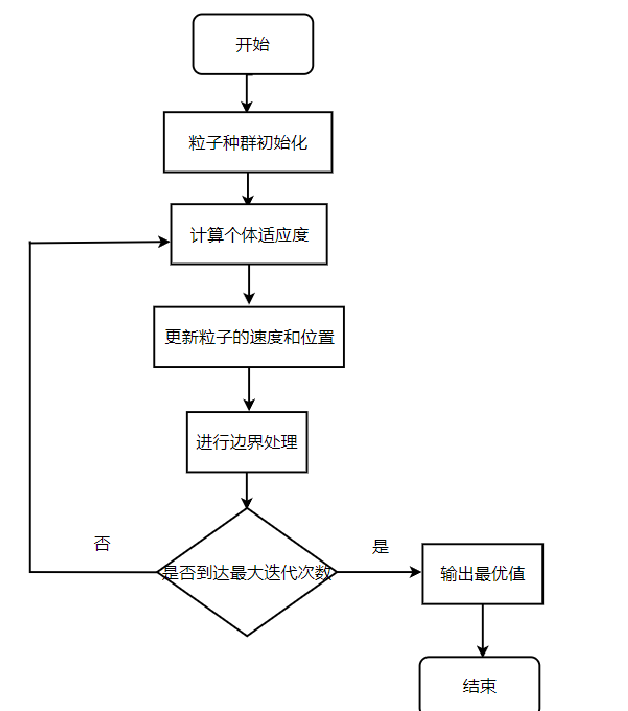
算法的主要流程:
第一步:對粒子群的隨機位置和速度進行初始設定,同時設定迭代次數。
第二步:計算每個粒子的適應度值。
第三步:對每個粒子,將其適應度值與所經歷的最好位置pbest i的適應度值進行比較,若較好,則將其作為當前的個體最優位置。
第四步:對每個粒子,將其適應度值與全局所經歷的最好位置gbestg的適應度值進行比較,若較好,則將其作為當前的全局最優位置。
第五步:根據速度、位置公式對粒子的速度和位置進行優化,從而更新粒子位置。
第六步:如未達到結束條件(通常為最大循環數或最小誤差要求),則返回第二步
優點:
PSO算法沒有交叉和變異運算,依靠粒子速度完成搜索,并且在迭代進化中只有最優的粒子把信息傳遞給其它粒子,搜索速度快。
PSO算法具有記憶性,粒子群體的歷史最好位置可以記憶并傳遞給其它粒子。
需調整的參數較少,結構簡單,易于工程實現。
采用實數編碼,直接由問題的解決定,問題解的變量數直接作為粒子的維數。
缺點:
缺乏速度的動態調節,容易陷入局部最優,導致收斂精度低和不易收斂。
不能有效解決離散及組合優化問題。
參數控制,對于不同的問題,如何選擇合適的參數來達到最優效果。
不能有效求解一些非直角坐標系描述問題,
ok,我們來看一下最簡單的實現:
import numpy as np
import random
class PSO_model:
def __init__(self,w,c1,c2,r1,r2,N,D,M):
self.w = w # 慣性權值
self.c1=c1
self.c2=c2
self.r1=r1
self.r2=r2
self.N=N # 初始化種群數量個數
self.D=D # 搜索空間維度
self.M=M # 迭代的最大次數
self.x=np.zeros((self.N,self.D)) #粒子的初始位置
self.v=np.zeros((self.N,self.D)) #粒子的初始速度
self.pbest=np.zeros((self.N,self.D)) #個體最優值初始化
self.gbest=np.zeros((1,self.D)) #種群最優值
self.p_fit=np.zeros(self.N)
self.fit=1e8 #初始化全局最優適應度
# 目標函數,也是適應度函數(求最小化問題)
def function(self,x):
A = 10
x1=x[0]
x2=x[1]
Z = 2 * A + x1 ** 2 - A * np.cos(2 * np.pi * x1) + x2 ** 2 - A * np.cos(2 * np.pi * x2)
return Z
# 初始化種群
def init_pop(self):
for i in range(self.N):
for j in range(self.D):
self.x[i][j] = random.random()
self.v[i][j] = random.random()
self.pbest[i] = self.x[i] # 初始化個體的最優值
aim=self.function(self.x[i]) # 計算個體的適應度值
self.p_fit[i]=aim # 初始化個體的最優位置
if aim < self.fit: # 對個體適應度進行比較,計算出最優的種群適應度
self.fit = aim
self.gbest = self.x[i]
# 更新粒子的位置與速度
def update(self):
for t in range(self.M): # 在迭代次數M內進行循環
for i in range(self.N): # 對所有種群進行一次循環
aim=self.function(self.x[i]) # 計算一次目標函數的適應度
if aim<self.p_fit[i]: # 比較適應度大小,將小的負值給個體最優
self.p_fit[i]=aim
self.pbest[i]=self.x[i]
if self.p_fit[i]<self.fit: # 如果是個體最優再將和全體最優進行對比
self.gbest=self.x[i]
self.fit = self.p_fit[i]
for i in range(self.N): # 更新粒子的速度和位置
self.v[i]=self.w*self.v[i]+self.c1*self.r1*(self.pbest[i]-self.x[i])+ self.c2*self.r2*(self.gbest-self.x[i])
self.x[i]=self.x[i]+self.v[i]
print("最優值:",self.fit,"位置為:",self.gbest)
if __name__ == '__main__':
# w,c1,c2,r1,r2,N,D,M參數初始化
w=random.random()
c1=c2=2#一般設置為2
r1=0.7
r2=0.5
N=30
D=2
M=200
pso_object=PSO_model(w,c1,c2,r1,r2,N,D,M)#設置初始權值
pso_object.init_pop()
pso_object.update()首先這個使用PSO的話,其實是和我們的這個先前使用遺傳是類似的,我們依然通過一個矩陣表示種群,一個矩陣表示城市之間的距離。
# 群體的初始化和路徑的初始化 self.population = np.array([0] * self.num_pop * self.num).reshape( self.num_pop, self.num) self.fitness = [0] * self.num_pop """ 計算城市的距離,我們用矩陣表示城市間的距離 """ self.__matrix_distance = self.__matrix_dis()
和我們原來的PSO的最大區別是啥呢,其實和簡單,在與我們速度的更新。我們在連續問題的時候其實是這樣的:
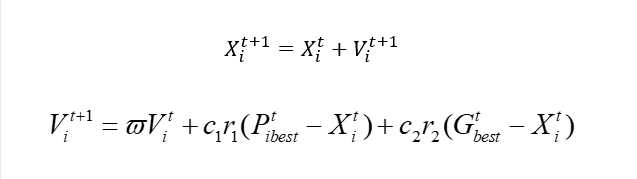
同樣的我們可以把X表示城市的編號,但是顯然我們不能使用這種方案進行速度的更新。
那么這個時候,我們對于速度的更新的話,我們是需要使用到一種新的方案,那么這個方案的話其實就是套用遺傳算算法的X更新。我們之所以需要速度說白了就是為了更新X,讓X往好的方向進行瞎蒙。現在單純使用速度更新是不行了,那么反正都是更新X,選擇一個可以很好更新這個X的方案不就行了嘛。所以的話這里可直接使用遺傳啊,我們的速度更新是參考Pbest和Gbest,之后按照一定的權重進行“學習”這樣一來這個V就具備了Pbest和Gbest的一種“特征”。所以既然如此,那么我直接仿造遺傳交叉的時候和Best進行交叉不就可以學習到一些對應的“特征”嘛。
def cross_1(self, path, best_path): r1 = np.random.randint(self.num) r2 = np.random.randint(self.num) while r2 == r1: r2 = np.random.randint(self.num) left, right = min(r1, r2), max(r1, r2) cross = best_path[left:right + 1] for i in range(right - left + 1): for k in range(self.num): if path[k] == cross[i]: path[k:self.num - 1] = path[k + 1:self.num] path[-1] = 0 path[self.num - right + left - 1:self.num] = cross return path
同時我們依然可以引入變異。
def mutation(self,path): r1 = np.random.randint(self.num) r2 = np.random.randint(self.num) while r2 == r1: r2 = np.random.randint(self.num) path[r1],path[r2] = path[r2],path[r1] return path
ok,現在我們來看到完整的代碼:
import numpy as np
import matplotlib.pyplot as plt
class HybridPsoTSP(object):
def __init__(self ,data ,num_pop=200):
self.num_pop = num_pop # 群體個數
self.data = data # 城市坐標
self.num =len(data) # 城市個數
# 群體的初始化和路徑的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
計算城市的距離,我們用矩陣表示城市間的距離
"""
self.__matrix_distance = self.__matrix_dis()
def __matrix_dis(self):
"""
計算14個城市的距離,將這些距離用矩陣存起來
:return:
"""
res = np.zeros((self.num, self.num))
for i in range(self.num):
for j in range(i + 1, self.num):
res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
res[j, i] = res[i, j]
return res
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return path
def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return path
def comp_fit(self, one_path):
"""
計算,咱們這個路徑的長度,例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def out_path(self, one_path):
"""
輸出我們的路徑順序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.num):
res += str(one_path[i] + 1) + '-->'
res += str(one_path[0] + 1) + '\n'
print(res)
def init_population(self):
"""
初始化種群
:return:
"""
rand_ch = np.array(range(self.num))
for i in range(self.num_pop):
np.random.shuffle(rand_ch)
self.population[i, :] = rand_ch
self.fitness[i] = self.comp_fit(rand_ch)
def main(data, max_n=200, num_pop=200):
Path_short = HybridPsoTSP(data, num_pop=num_pop) # 混合粒子群算法類
Path_short.init_population() # 初始化種群
# 初始化路徑繪圖
fig, ax = plt.subplots()
x = data[:, 0]
y = data[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(data) + 1)):
ax.annotate(txt, (x[i], y[i]))
res0 = Path_short.population[0]
x0 = x[res0]
y0 = y[res0]
for i in range(len(data) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
print('初始染色體的路程: ' + str(Path_short.fitness[0]))
# 存儲個體極值的路徑和距離
best_P_population = Path_short.population.copy()
best_P_fit = Path_short.fitness.copy()
min_index = np.argmin(Path_short.fitness)
# 存儲當前種群極值的路徑和距離
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 存儲每一步迭代后的最優路徑和距離
best_population = [best_G_population]
best_fit = [best_G_fit]
# 復制當前群體進行交叉變異
x_new = Path_short.population.copy()
for i in range(max_n):
# 更新當前的個體極值
for j in range(num_pop):
if Path_short.fitness[j] < best_P_fit[j]:
best_P_fit[j] = Path_short.fitness[j]
best_P_population[j, :] = Path_short.population[j, :]
# 更新當前種群的群體極值
min_index = np.argmin(Path_short.fitness)
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 更新每一步迭代后的全局最優路徑和解
if best_G_fit < best_fit[-1]:
best_fit.append(best_G_fit)
best_population.append(best_G_population)
else:
best_fit.append(best_fit[-1])
best_population.append(best_population[-1])
# 將每個個體與個體極值和當前的群體極值進行交叉
for j in range(num_pop):
# 與個體極值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_P_population[j, :])
fit = Path_short.comp_fit(x_new[j, :])
# 判斷是否保留
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 與當前極值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_G_population)
fit = Path_short.comp_fit(x_new[j, :])
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 變異
x_new[j, :] = Path_short.mutation(x_new[j, :])
fit = Path_short.comp_fit(x_new[j, :])
if fit <= Path_short.fitness[j]:
Path_short.population[j] = x_new[j, :]
Path_short.fitness[j] = fit
if (i + 1) % 20 == 0:
print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[min_index]))
print('第' + str(i + 1) + '步后的最優路徑:')
Path_short.out_path(Path_short.population[min_index, :]) # 顯示每一步的最優路徑
Path_short.best_population = best_population
Path_short.best_fit = best_fit
return Path_short # 返回結果類
if __name__ == '__main__':
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
main(data)初始染色體的路程: 71.30211569672313
第20步后的最短的路程: 29.340520066994223
第20步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第40步后的最短的路程: 29.340520066994223
第40步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第60步后的最短的路程: 29.340520066994223
第60步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第80步后的最短的路程: 29.340520066994223
第80步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第100步后的最短的路程: 29.340520066994223
第100步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第120步后的最短的路程: 29.340520066994223
第120步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第140步后的最短的路程: 29.340520066994223
第140步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第160步后的最短的路程: 29.340520066994223
第160步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第180步后的最短的路程: 29.340520066994223
第180步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第200步后的最短的路程: 29.340520066994223
第200步后的最優路徑:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
可以看到收斂速度還是很快的。
ok,到目前為止的話,我們介紹了兩個算法去解決TSP或者是優化問題。我們來分析一下,這些算法有什么特點,為啥可以達到我們需要的優化效果。其實不管是遺傳還是PSO,你其實都可以發現,有一個東西,我們可以暫且叫它環境壓力。我們通過物競天擇,或者鳥類遷移,進行模擬尋優。而之所以需要這樣做,是因為我們指定了一個規則,在我們的規則之下。我們讓模擬的種群有一種壓力去靠攏,其中物競天擇和鳥類遷移只是我們的一種手段,去應對這樣的“壓力”。所以的對于這種算法而言,最核心的點就兩個:
我們需要做優化問題,所以我們必須要能夠讓我們的解往那個方向走,需要一個驅動,需要一個壓力。因此我們需要設計這樣的一個環境,在遺傳算法,粒子群算法是通過種群當中的生存,來進行設計的它的壓力是我們的目標函數。由種群和目標函數(目標指標)構成了一個環境和壓力。
之后的話,我們設計好了一個環境和壓力,那么未來應對這種壓力,我們需要去設計一種策略,來應付這種壓力。遺傳算法是通過PUA自己,也就是種群的優勝略汰。PSO是通過學習,學習種群的優秀粒子和過去自己家的優秀“祖先”來應對這種壓力的。
所以的話,我們是否可以使用別的方案來實現這種優化效果。,在強化學習的算法框架里面的話,我們明確的知道了為什么他們可以實現優化,是環境壓力+壓力策略。恰好咱們強化學習是有環境的,適應函數和環境恰好可以組成環境+壓力。本身的算法收斂過程就是我們的壓力策略。所以我們完全是可以直接使用強化學習進行這個處理的。那么在這里咱們就來使用強化學習在下一篇文章當中。
關于“怎么使用Python PSO算法處理TSP問題”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“怎么使用Python PSO算法處理TSP問題”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。