基于Pytorch如何實現邏輯回歸

本篇內容主要講解“基于Pytorch如何實現邏輯回歸”，感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷，實用性強。下面就讓小編來帶大家學習“基于Pytorch如何實現邏輯回歸”吧!

1.邏輯回歸

線性回歸表面上看是“回歸問題”，實際上處理的問題是“分類”問題，邏輯回歸模型是一種廣義的回歸模型，其與線性回歸模型有很多的相似之處，模型的形式也基本相同，唯一不同的地方在于邏輯回歸會對y作用一個邏輯函數，將其轉化為一種概率的結果。邏輯函數也稱為Sigmoid函數，是邏輯回歸的核心。

2.基于Pytorch實現邏輯回歸

import torch as t
import matplotlib.pyplot as plt
from torch import nn
from torch.autograd import Variable
import numpy as np
 
 
# 構造數據集
n_data = t.ones(100, 2)
# normal（）返回一個張量，張量里面的隨機數是從相互獨立的正態分布中隨機生成的。
x0 = t.normal(2*n_data, 1)
y0 = t.zeros(100)
x1 = t.normal(-2*n_data, 1)
y1 = t.ones(100)
 
# 把數據給合并以下，并且數據的形式必須是下面形式
x = t.cat((x0, x1), 0).type(t.FloatTensor)
y = t.cat((y0, y1), 0).type(t.FloatTensor)
 
# 觀察制造的數據
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0)
plt.show()
 
# 建立邏輯回歸
class LogisticRegression(nn.Module):
    def __init__(self):
        super(LogisticRegression, self).__init__()
        self.lr = nn.Linear(2, 1)
        self.sm = nn.Sigmoid()
    def forward(self, x):
        x = self.lr(x)
        x = self.sm(x)
        return x
# 實例化
logistic_model = LogisticRegression()
# 看GPU是否可使用，如果可以使用GPU否則不使用
if t.cuda.is_available():
    logistic_model.cuda()
# 定義損失函數和優化函數
criterion = nn.BCELoss()
optimizer = t.optim.SGD(logistic_model.parameters(), lr=1e-3, momentum=0.9)
# 訓練模型
for epoch in range(1000):
    if t.cuda.is_available():
        x_data = Variable(x).cuda()
        y_data = Variable(y).cuda()
    else:
        x_data = Variable(x)
        y_data = Variable(y)
        out = logistic_model(x_data)
        loss = criterion(out, y_data)
        print_loss = loss.data.item()
        # 以0.5為閾值進行分類
        mask = out.ge(0.5).float()
        # 計算正確預測樣本的個數
        correct = (mask==y_data).sum()
        # 計算精度
        acc = correct.item()/x_data.size(0)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        # 每個200個epoch打印一次當前的誤差和精度
        if(epoch+1)%200==0:
            print('*'*10)
            # 迭代次數
            print('epoch{}'.format(epoch+1))
            # 誤差
            print('loss is {:.4f}'.format((print_loss)))
            # 精度
            print('acc is {:.4f}'.format(acc))
if __name__=="__main__":
    logistic_model.eval()
    w0, w1 = logistic_model.lr.weight[0]
    w0 = float(w0.item())
    w1 = float(w1.item())
    b = float(logistic_model.lr.bias.item())
    plot_x = np.arange(-7, 7, 0.1)
    plot_y = (-w0*plot_x-b)/w1
    plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0)
    plt.plot(plot_x, plot_y)
    plt.show()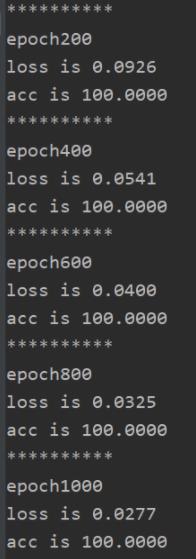

到此，相信大家對“基于Pytorch如何實現邏輯回歸”有了更深的了解，不妨來實際操作一番吧！這里是億速云網站，更多相關內容可以進入相關頻道進行查詢，關注我們，繼續學習！