Python中如何實現支持向量機數據分類和回歸預測

這篇文章主要為大家展示了“Python中如何實現支持向量機數據分類和回歸預測”，內容簡而易懂，條理清晰，希望能夠幫助大家解決疑惑，下面讓小編帶領大家一起研究并學習一下“Python中如何實現支持向量機數據分類和回歸預測”這篇文章吧。

支持向量機常用于數據分類，也可以用于數據的回歸預測

1、Question?

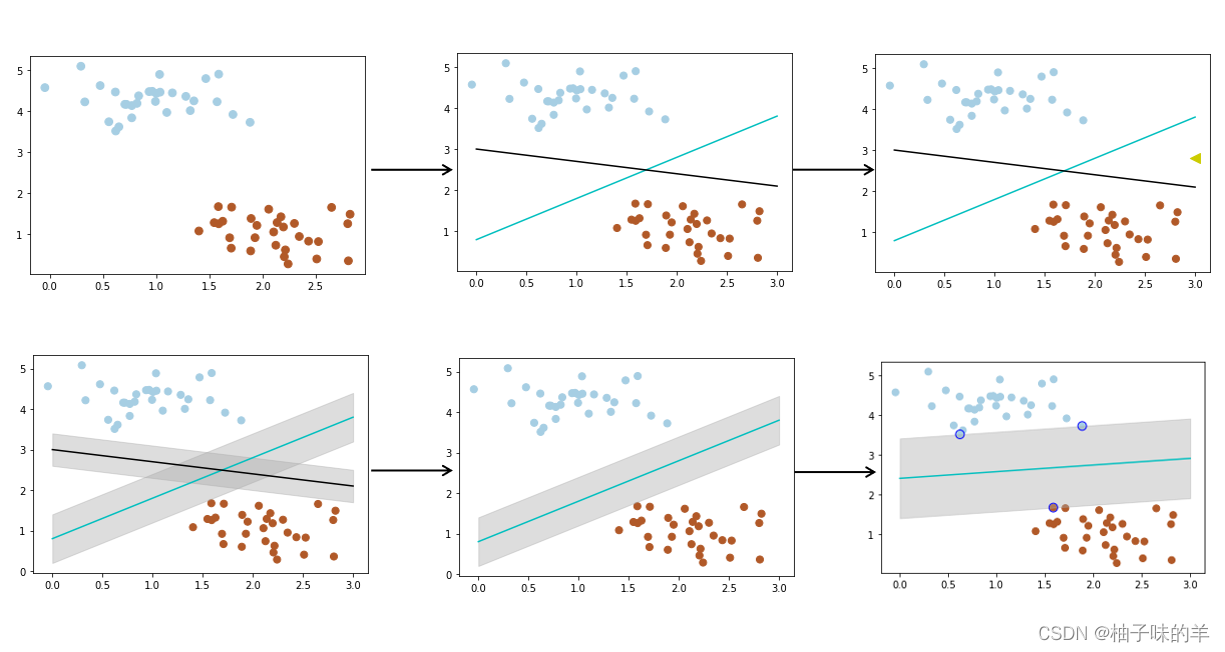
我們經常會遇到這樣的問題，給你一些屬于兩個類別的數據（如子圖1），需要一個線性分類器將這些數據分開,有很多分法（如子圖2），現在有一個問題，兩個分類器，哪一個更好？為了判斷好壞，我們需要引入一個準則：好的分類器不僅僅能夠很好的分開已有的數據集，還能對為知的數據進行兩個劃分，假設現在有一個屬于紅色數據點的新數據（如子圖3中的綠三角），可以看到此時黑色的線會把這個新的數據集分錯，而藍色的線不會。**那么如何評判兩條線的健壯性？**此時，引入一個重要的概念——最大間隔（刻畫著當前分類器與數據集的邊界）（如子圖4中的陰影部分）可以看到藍色的線最大的間隔大于黑色的線，所以選擇藍色的線作為我們的分類器。（如子圖5）此時的分類器是最優分類器嗎？或者說，有沒有更好的分類器具有更大的間隔？有的（如子圖6）為了找到最優分類器，引入SVM

2、Answer！——SVM

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
x_fit = np.linspace(0, 3)
#使用SVM
from sklearn.svm import SVC
# SVM 函數
clf = SVC(kernel='linear')
clf.fit(X, y)
# 最佳函數
w = clf.coef_[0]
a = -w[0] / w[1]
y_p = a*x_fit - (clf.intercept_[0]) / w[1]

# 最大邊距 下邊界
b_down = clf.support_vectors_[0]
y_down = a* x_fit + b_down[1] - a * b_down[0]
# 最大邊距 上屆
b_up = clf.support_vectors_[-1]
y_up = a* x_fit + b_up[1] - a * b_up[0]

# 畫散點圖
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 畫函數
plt.plot(x_fit, y_p, '-c')
# 畫邊距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 畫支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
            s=80, facecolors='none')

運行結果

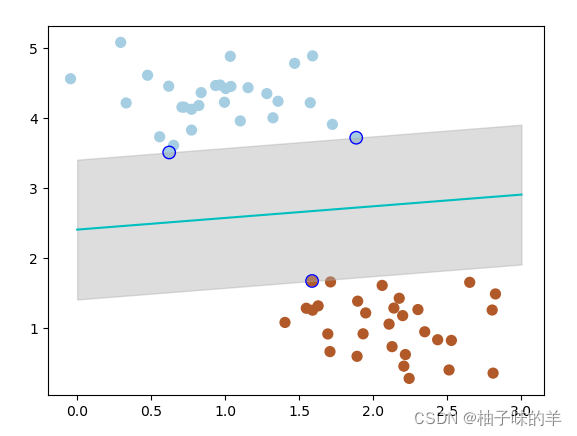
其中帶邊線的是距離當前分類器最近的點，將這些點稱之為支持向量，支持向量機為我們在眾多可能的分類器之間進行選擇的原則，從而確保對為知數據集具有更高的泛化性

3、軟間隔

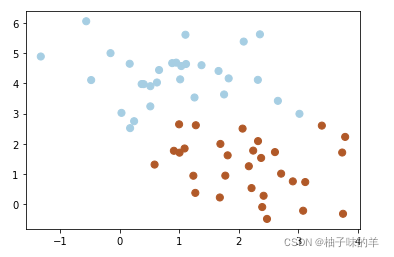
在很多時候，我們拿到是數據不想上述那樣分明（如下圖）這種情況并不容易找到上述那樣的最大間隔。于是就有了軟間隔，相對于硬間隔，我們允許個別數據出現在間隔帶中。我們知道，如果沒有一個原則進行約束，滿足軟間隔的分類器也會出現很多條。所以需要對分錯的數據進行懲罰，SVM函數，有一個參數C就是懲罰參數。懲罰參數越小，容忍性就越大

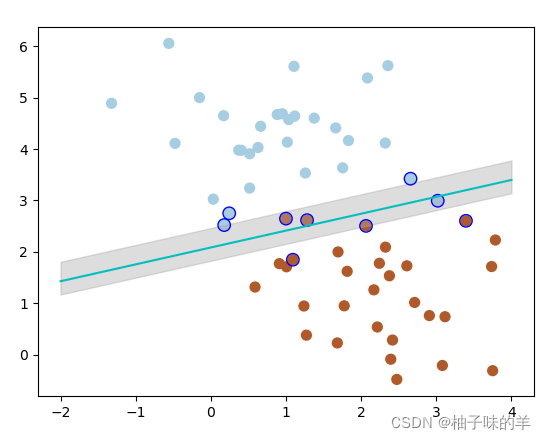
——此處C設置為1

#%%軟間隔
X, y = make_blobs(n_samples=60, centers=2, random_state=0, cluster_std=0.9)
x_fit = np.linspace(-2, 4)
# 懲罰參數：C=1，
clf = SVC(C=1, kernel='linear')
clf.fit(X, y)

# 最佳函數
w = clf.coef_[0]
a = -w[0] / w[1]
y_great = a*x_fit - (clf.intercept_[0]) / w[1]
# 最大邊距 下邊界
b_down = clf.support_vectors_[0]
y_down = a* x_fit + b_down[1] - a * b_down[0]
# 最大邊距 上邊界
b_up = clf.support_vectors_[-1]
y_up = a* x_fit + b_up[1] - a * b_up[0]
# 畫散點圖
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
# 畫函數
plt.plot(x_fit, y_great, '-c')
# 畫邊距
plt.fill_between(x_fit, y_down, y_up, edgecolor='none', color='#AAAAAA', alpha=0.4)
# 畫支持向量
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',
            s=80, facecolors='none')

運行結果

——當將C設置為0.2時，SVM會更有包容性，從而兼容更多的錯分樣本，結果如下：

4、超平面

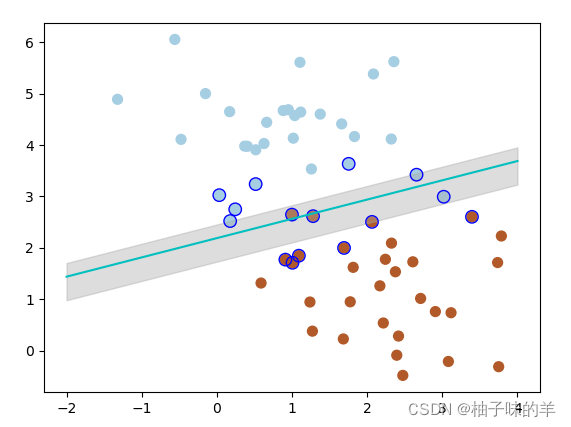
有時，我們得到的數據是這樣的（如下圖），這時，可以將二維空間（低維）的數據映射到三維空間（高維）中，此時，可以通過一個超平面對數據進行劃分，所以，映射的目的在于使用SVM在高維空間找到超平面的能力

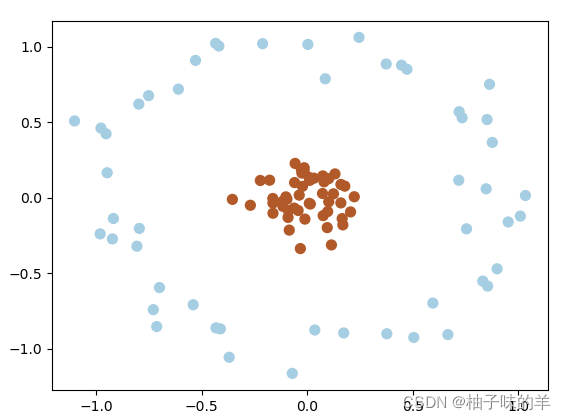
#%%超平面
from sklearn.datasets import make_circles
# 畫散點圖
X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)

# 數據映射
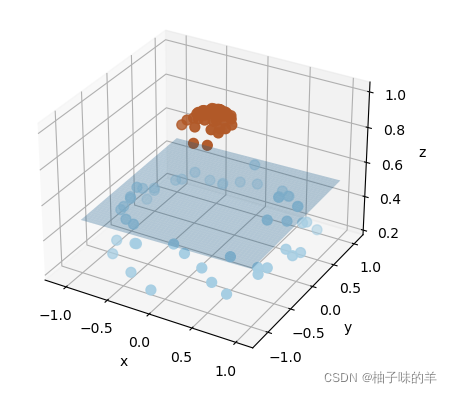
r = np.exp(-(X[:, 0] ** 2 + X[:, 1] ** 2))

ax = plt.subplot(projection='3d')
ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap=plt.cm.Paired)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')

x_1, y_1 = np.meshgrid(np.linspace(-1, 1), np.linspace(-1, 1))
z =  0.01*x_1 + 0.01*y_1 + 0.5
ax.plot_surface(x_1, y_1, z, alpha=0.3)

運行結果

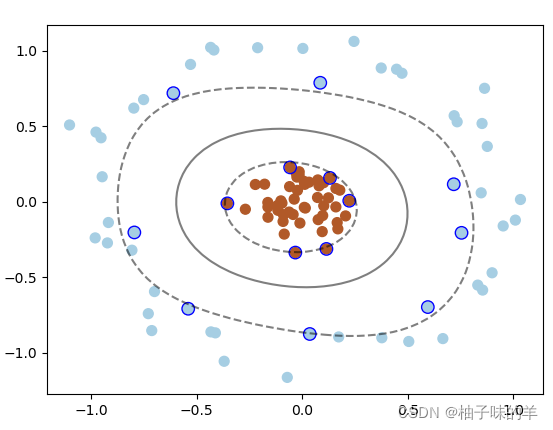
使用高斯核函數實現這種情形的分類

#%%使用高斯核函數實現這種分類：kernel=‘rbf'
# 畫圖
X, y = make_circles(100, factor=.1, noise=.1, random_state=2019)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.Paired)
clf = SVC(kernel='rbf')
clf.fit(X, y)

ax = plt.gca()
x = np.linspace(-1, 1)
y = np.linspace(-1, 1)
x_1, y_1 = np.meshgrid(x, y)
P = np.zeros_like(x_1)
for i, xi in enumerate(x):
    for j, yj in enumerate(y):
        P[i, j] = clf.decision_function(np.array([[xi, yj]]))
ax.contour(x_1, y_1, P, colors='k', levels=[-1, 0, 0.9], alpha=0.5,linestyles=['--', '-', '--'])
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], edgecolor='b',s=80, facecolors='none');

運行結果

以上是“Python中如何實現支持向量機數據分類和回歸預測”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！