Python光學仿真教程怎么實現光線追蹤

本篇內容主要講解“Python光學仿真教程怎么實現光線追蹤”，感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷，實用性強。下面就讓小編來帶大家學習“Python光學仿真教程怎么實現光線追蹤”吧!

光線追跡

得益于計算機的計算的能力，通過追蹤具有代表性的光線的傳播軌跡，可以更加精確地描述光學系統的性能，光線追跡方法也因此大展其能，諸如Zemax、tracepro等軟件便都提供了相應的功能。

而建立在折射定律基礎之上的光線追跡方法，對數學功底要求較低，所以比較適合作為python初學者的入門項目。在接下來的這一章，希望通過對光線追跡的實現，掌握python中的列表、元組、字典、集合等數據類型的基本概念，并且對面向對象與函數式編程有一個基本的了解。

幾何抽象

光線

光線追跡描述的是光線與光學元件接觸之后的行為變化，因此首先需要對光線與光學元件進行刻劃。由于我們希望最終建立一個二維的光路系統，光線既可能水平，也可能豎直，因此通過 a x + b y + c = 0 來表示一條光線。即只需$a b c $這三個數字，便可以確定二維空間中的一條直線。

在python中，可以通過序列-list來表示一組數據，在list中，每個元素都分配一個數字作為索引，可以通過索引來提取或改變list中的值。需要注意的是，和諸多編程語言類似，python中的索引也是從0開始的。所以我們可以在python中新建一個變量來表示一條過原點斜率為1的直線：

>>> abc=[1,-1,0]    #在python中，list用方括號表示
>>> type(abc)       #type函數可以返回數據類型
<class 'list'>
>>> abc[0]          #在python中，用方括號進行索引
1
>>> abc[1] = 5      #list中的值可以更改
>>> abc[-1]         #在python中，索引-1往往表示倒數第一個值
0
>>> abc             #修改后的abc
[1, 5, 0]

當然，光線實質上是一種有源的射線，所以需要對直線方程 a x + b y + c = 0 進行符號約定，進而明確其方向性。
考慮到[a,b,c]與[-a,-b,-c]可以表示同一條直線，所以我們可以通過 a 和 b的正負號來表明其方向。通過射線終點所在象限對[a,b]的正負號進行限定，可以得到幾組不同的符號約定，在此我們選取如下約定：

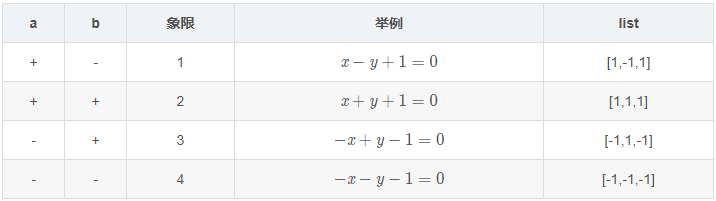
可以看到第一、三條射線的方程表示同一條直線，但由于引入符號約定，所以我們可以區分其方向上的差別，從而可以判斷這條光線是否會與某一光學元件相交。

如果希望繪制出一條光線，可以調用python的UI庫wxpython，為了不影響內容的連貫性，這種方法會在后面統一講解。

除了這里所推薦的直線的abc表示法，我們還可以通過始點與角度來對光線進行表示，我們同樣可以使用三個參數[x0,y0,theta]。但是在進行計算的時候，需要先將其轉換成為[a,b,c]的表示方法，因此需要定義轉換函數，即通過初始點和角度生成射線的函數，考慮到此前的符號約定，其轉換公式為

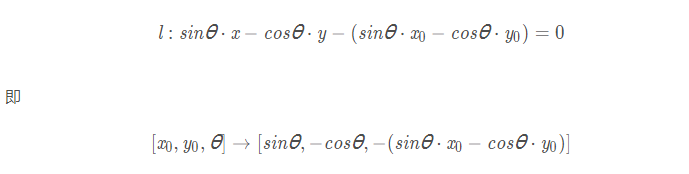
需要注意的一點是，這里需要調用numpy包來使用三角函數。

import numpy as np
x0,y0,theta = [0,0,np.pi/4]     #np.pi即圓周率
abc = [np.sin(theta),           #在python中，括號內換行可以不用標記
      -np.cos(theta),
      -(np.sin(theta)*x0-np.cos(theta)*y0)]

由于這個方法可能會被經常使用，所以可以封裝成函數，在python中，通過關鍵字def進行函數的定義。對于參數個數和返回值的個數以及數據類型幾乎沒有限制。故可以寫為

import numpy as np
def getABC(x0,y0,theta):    #函數定義格式為 def 函數名(傳入參數):
    a = np.sin(theta)       #函數下方需要進行縮進
    b = -np.cos(theta)
    c = -(np.sin(theta)*x0-np.cos(theta)*y0)
return a,b,c                #在python中，通過return返回abc參數

也可以寫為

import numpy as np
def getABC(x0,y0,theta):
    return [np.sin(theta),      #在括號內可以直接換行
            -np.cos(theta),
            -(np.sin(theta)*x0-np.cos(theta)*y0)]

在命令行中調用

>>> import test
>>> import numpy as np
>>> test.getABC(0,0,-np.pi/4)
[-0.7071067811865476, -0.7071067811865476, 0.0]

線段與圓弧

在光學系統中，最常見的光學器件便是平面鏡和透鏡，則其在入射光線子午面上的投影可拆解為線段和圓弧。

對于線段，可以非常直觀地通過兩個點進行表示。在python中，除了列表之外，可以用元組(tuple)來表示序列，不同之處在于元組的元素不能修改。在此，用飽含兩個元素的元組來表示一個點,將兩個點組成列表來表示線段：

>>> a = (0,0)       #在python中，元組用小括號表示
>>> b = (1,1)
>>> seg = [a,b]     #列表中的元素可以有不同的類型
>>> seg
[(0, 0), (1, 1)]
>>>

圓可以通過圓心與半徑來表示，簡潔而利于計算。圓弧則可以通過圓與角度來表示。但是作為光學元件的組成部分，為了便于后面的處理，其表現形式最好與線段相似，即通過三點即A、B、C來確認一段圓弧。

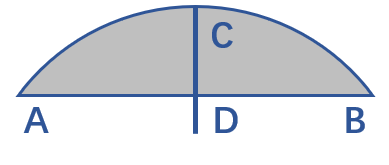
但是具體計算的過程中往往需要將圓弧轉換成圓的表達形式進行操作，所以定義函數arc2cir來實現這個功能。由于其數學過程過于簡單，故只對一些命令進行說明，其中np.lialg為numpy的線性代數包，np.linalg.norm為求范數，np.linalg.norm(a-b)相當于求a、b兩點之間的距離。

def arc2cir(arc):
    arc = np.array(arc)     #list不能進行數組運算，需要轉成np.array的形式
    dCD = np.linalg.norm(1/2*(arc[0]+arc[1])-arc[2])  #CD長度
    dBC2 = np.sum(np.square(arc[1]-arc[2]))           #BC**2
    radius = 0.5*dBC2/dCD                             #圓半徑
    theta = (arc[2]-1/2*(arc[0]+arc[1]))/dCD          #三角函數值
    zero = arc[2]-radius*theta
    return list(zero)+[radius]                        #列表相加為其內部元素的合并

需要注意的是，在python中，list、tuple都不支持整體上的數學計算，這很容易理解，因為二者中存儲的不一定是數字，而可能是其他的什么東西。格式不同，自然無法計算。因此在考慮計算之前，需要將二者轉換成numpy.array這種數組格式。

列表、元組、數組之間的轉換非常簡單而直觀。

import numpy as np
>>> lis = [1,2,3]
>>> tup = tuple(lis)
>>> arr = np.array(tup)
>>> arr
array([1, 2, 3])
>>> lis
[1, 2, 3]
>>> tup
(1, 2, 3)

到此，相信大家對“Python光學仿真教程怎么實現光線追蹤”有了更深的了解，不妨來實際操作一番吧！這里是億速云網站，更多相關內容可以進入相關頻道進行查詢，關注我們，繼續學習！