您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“怎么改進Python二分法和牛頓迭代法求算術平方根”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“怎么改進Python二分法和牛頓迭代法求算術平方根”吧!
二分法
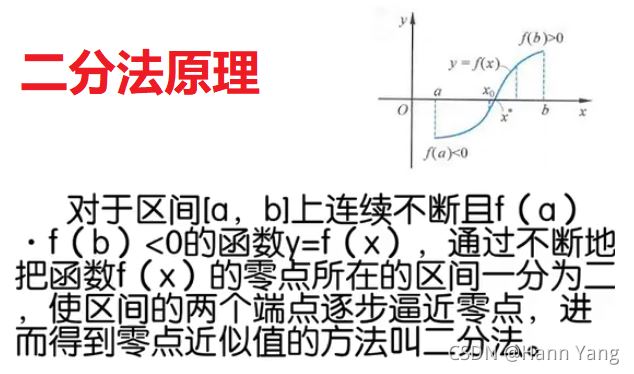
二分法原理
牛頓迭代法
牛頓迭代法原理
def sqrtb(n):
if n<0: raise ValueError('n>=0')
left,right,x=0,n,n/2
while not -1e-15<x*x-n<1e-15:
if x*x>n:
right,x = x,left+(x-left)/2
else:
left,x = x,right-(right-x)/2
return x求最接近算術平方根的整數
def sqrtB(x): if x==0: return 0 #y,x=x,round(x) left,right,ret = 1,x,0 while left<=right: mid = left + (right-left)//2 if mid<x/mid: left = mid+1 ret = mid elif mid==x/mid: ret = mid break else: right = mid-1 return ret
>>> sqrtB(9)
3
>>> sqrtB(8)
2
>>> sqrtB(9.2)
3.0
>>> sqrtB(7.8)
2.0
>>> sqrtB(4)
2
>>>
def sqrtn(n):
if n<0: raise ValueError('n>=0')
x = n/2
while not -1e-15<x*x-n<1e-15:
x = (x+n/x)/2
return x一點小改進:不用1e-15來比較
def sqrt2(n): x = n while x*x>n: x = (x+n/x)/2 return x
缺點:碰到n=7,13,...等,會進入死循環
增加判斷跳出循環:
def sqrt(n): x = n while x*x>n: y,x = x,(x+n/x)/2 if y==x: break return x
# sqrt(n) n=1~25的精度測試:
0.0
-2.220446049250313e-16
0.0
0.0
0.0
0.0
0.0
-4.440892098500626e-16
0.0
-4.440892098500626e-16
0.0
0.0
4.440892098500626e-16
0.0
0.0
0.0
0.0
8.881784197001252e-16
-8.881784197001252e-16
0.0
0.0
0.0
0.0
0.0
0.0
>>>
從函數意義上理解:要求函數f(x)=x²,使f(x)=num的近似解,即x²-num=0的近似解。
從幾何意義上理解:要求拋物線g(x)=x²-num與x軸交點(g(x)=0)最接近的點。
假設g(x0)=0,即x0是正解,讓近似解x不斷逼近x0,x0 ~ x - f(x)/f'(x)
def cubeN(n): x,y = n/3,0 while not -1e-15<x-y<1e-15: y,x = x,(2/3)*x+n/(3*x*x) return x ''' >>> cubeN(27) 3.0 >>> cubeN(9) 2.080083823051904 >>> '''
感謝各位的閱讀,以上就是“怎么改進Python二分法和牛頓迭代法求算術平方根”的內容了,經過本文的學習后,相信大家對怎么改進Python二分法和牛頓迭代法求算術平方根這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。