什么是紅黑樹

發布時間：2022-05-18 14:48:11 來源：億速云閱讀：148 作者：iii 欄目：大數據

這篇文章主要介紹“什么是紅黑樹”的相關知識，小編通過實際案例向大家展示操作過程，操作方法簡單快捷，實用性強，希望這篇“什么是紅黑樹”文章能幫助大家解決問題。

為什么要有紅黑樹

想必大家對二叉樹搜索樹都不陌生，首先看一下二叉搜索樹的定義：
二叉搜索樹（Binary Search Tree），或者是一棵空樹，或者是具有下列性質的二叉樹：若它的左子樹不空，則左子樹上所有結點的值均小于它的根結點的值；若它的右子樹不空，則右子樹上所有結點的值均大于它的根結點的值；它的左、右子樹也分別為二叉排序樹。
從理論上來說，二叉搜索樹的查詢、插入和刪除一個節點的時間復雜度均為O（log(n)）,已經完全可以滿足我們的要求了，那么為什么還要有紅黑樹呢？
我們來看一個例子，向二叉搜索樹中依次插入（1，2，3，4，5，6），插入之后是這樣的

可以看到，在這種情況下，二叉搜索樹退化成了鏈表！！！這時候查詢、插入和刪除一個元素的時候，時間復雜度變成了O（n），顯然這是不能接受的。出現這種情況情況的原因是二叉搜索樹沒有自平衡的機制，所以就有了平衡二叉樹的概念。
平衡二叉樹（Balanced Binary Tree）具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，并且左右兩個子樹都是一棵平衡二叉樹。
還是剛剛的例子，假如我們用平衡二叉樹來實現的話，插入完元素后應該是下面這樣的（不唯一）

平衡二叉樹保證了在最差的情況下，二叉樹依然能夠保持絕對的平衡，即左右兩個子樹的高度差的絕對值不超過1。但是這又會帶來一個問題，那就是平衡二叉樹的定義過于嚴格，導致每次插入或者刪除一個元素之后，都要去維護二叉樹整體的平衡，這樣產生額外的代價又太大了。二叉搜索樹可能退化成鏈表，而平衡二叉樹維護平衡的代價開銷又太大了，那怎么辦呢？這就要談到“中庸之道”的智慧了。說白了就是把平衡的定義適當放寬，不那么嚴格，這樣二叉樹既不會退化成鏈表，維護平衡的開銷也可以接受。沒錯，這就是我們要談的紅黑樹了。首先看一下紅黑樹的定義：
紅黑樹是一種含有紅黑結點并能自平衡的二叉查找樹。它必須除了滿足二叉搜索樹的性質外，還要滿足下面的性質：
性質1：每個節點要么是黑色，要么是紅色。
性質2：根節點是黑色。
性質3：每個葉子節點（NIL）是黑色。
性質4：每個紅色結點的兩個子結點一定都是黑色。
性質5：任意一結點到每個葉子結點的路徑都包含數量相同的黑結點。
這就是紅黑樹的五條性質。我相信很多人都看到過，能背下來的也不在少數，但是真正理解為什么要這樣定義的恐怕就不多了。下面就從2-3樹的角度來談談紅黑樹的定義。

從2-3樹來看紅黑樹

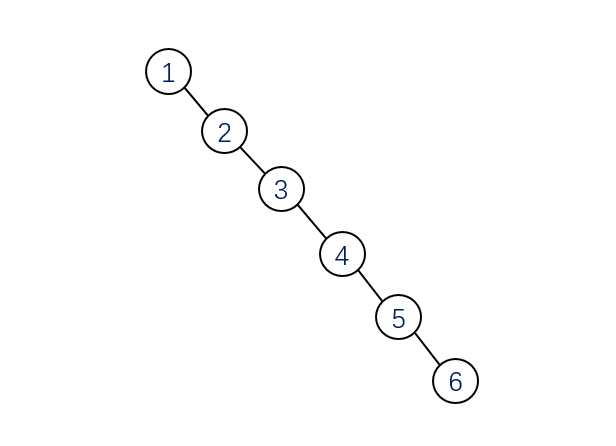
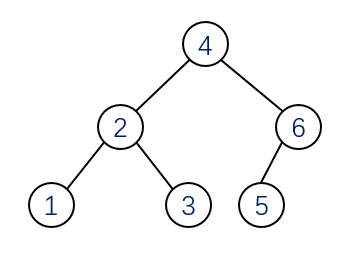
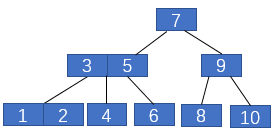
一般我們接觸最多的是二叉樹，也就是一個父節點最多有兩個子節點。2-3樹與二叉樹的不同之處在于，一個父節點可以有兩個子節點，也可以有三個子節點，并且其也滿足類似二叉搜索樹的性質。還有最重要的，2-3樹的所有葉子節點都在同一層，且最后一層不能有空節點，類似于滿二叉樹。
我們依次插入10，9，8，7，6，5，4，3，2，1來看一下2-3數是如何進行自平衡的。
2-3樹在插入元素之前首先要進行一次未命中的查找，然后將元素插入葉子節點中，之后再進行平衡操作，下面具體說明。
首先插入10，如下圖

然后插入9，9小于10，2-3樹在插入時要將9融入10這個葉子節點中（當然也是根節點），融合完成后如下：

這是一個3節點，不用執行平衡操作。2-3樹中把有兩個元素，三個子節點的節點稱為3節點，把有一個元素，兩個子節點的的節點稱為2節點。
接著插入8，插入8的時候同樣要先融入葉子節點中，如下圖左側所示

8融入葉子節點后，該結點便擁有了3個元素，不滿足2-3樹的定義，這時就要把3節點進行分裂，即把左側和右側的元素分裂為2節點，而中間的元素抽出，繼續融入其父節點，在這里便成為了一個根節點。
繼續插入7，如下

插入后，各個節點都滿足2-3樹的定義，不需要進行平衡操作。
接著插入6，還是首先找到葉子節點，然后將其融入，如下圖左側所示

插入后6、7、8三個元素所在的葉子節點不再滿足2-3樹的定義，需要進行分裂，即抽出元素7融入父節點，6和8分裂為7的左右子節點。
接著插入5，如下圖所示，同樣不需要進行平衡操作

接著插入4，還是首先找到葉子節點，然后將其融入，如下圖左側所示

插入后4、5、6三個元素所在的葉子節點不再滿足2-3樹的定義，需要進行分裂，即抽出元素5融入父節點，4和6分裂為5的左右子節點。5融入父節點后，該結點便有了5、7、9三個元素，因而需要繼續分裂，元素7成為新的根節點，5和9成為7的左右子節點。
接著插入3，3融入4所在的葉子節點中，不需要進行平衡操作

接著插入2，還是首先找到葉子節點，然后將其融入，如下圖左側所示

插入后2、3、4三個元素所在的葉子節點不再滿足2-3樹的定義，需要進行分裂，即抽出元素3融入父節點，2和4分裂為3的左右子節點，3融入5所在的父節點中。
最后插入2，同樣先找到葉子節點，然后將其融入，如下圖所示

至此，我們便完成了在2-3樹中依次插入10，9，8，7，6，5，4，3，2，1，并且2-3樹始終維護著平衡。怎么樣，是不是很神奇。

再看紅黑樹

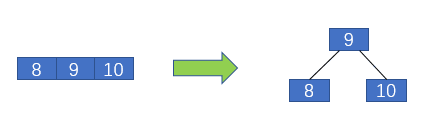
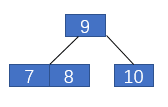
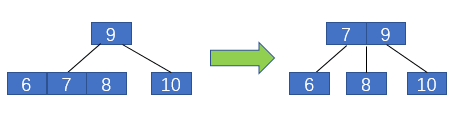
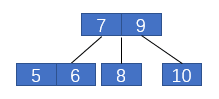
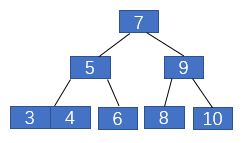
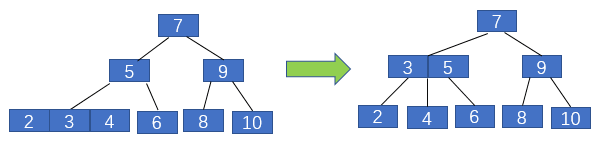
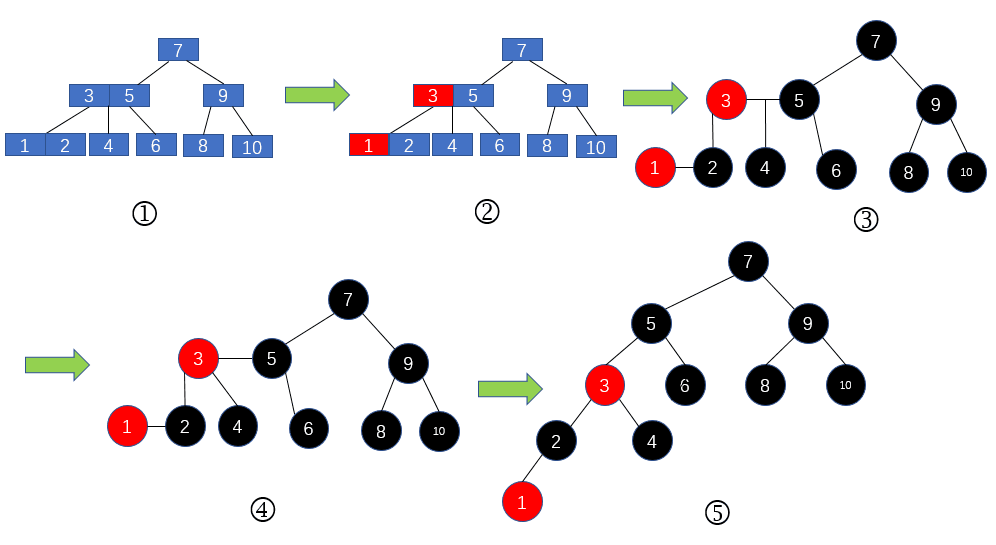
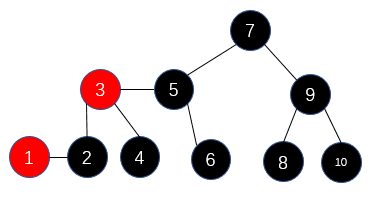
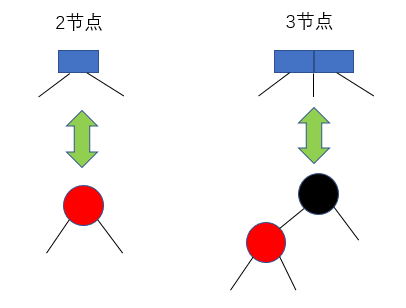
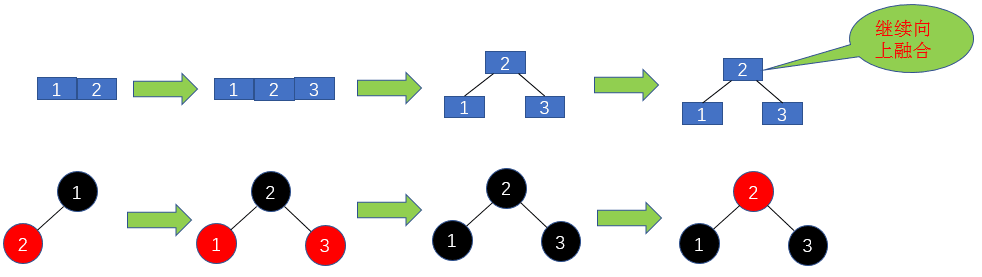
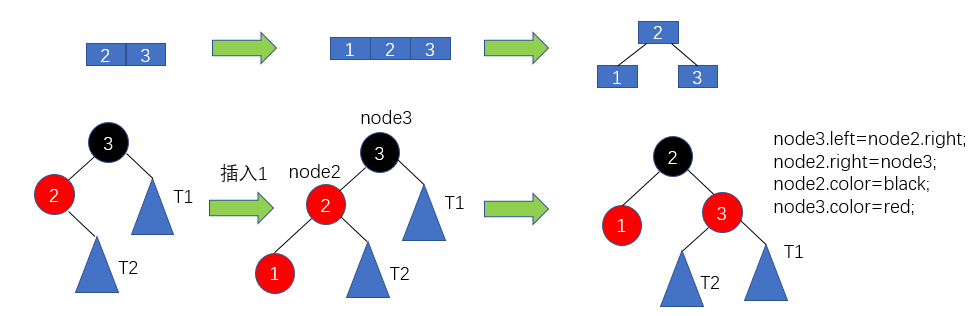
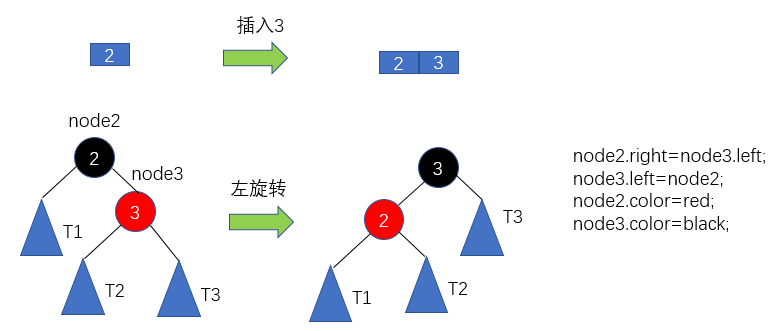
那么紅黑樹與2-3樹有什么關系呢？現在我們對2-3樹進行改造，改造成一個二叉樹。怎么改造呢？對于2節點，保持不變；對于3節點，我們首先將3節點中左側的元素標記為紅色，如下圖2所示。

然后我們將其改造成圖3的形式；再將3節點的位于中間的子節點的父節點設置為父節點中那個紅色的節點，如圖4的所示；最后我們將圖4的形式改為二叉樹的樣子，如圖5所示。圖5是不是很熟悉，沒錯，這就是我們常常提到的大名鼎鼎的紅黑樹了。
下面我們回過頭再看下紅黑樹的五條性質。

性質1：每個節點要么是黑色，要么是紅色。
2-3樹中存在2節點和3節點，3節點中左側的元素便是紅色節點，而其他的節點便是黑色節點。
性質2：根節點是黑色。
在2-3樹中，根節點只能是2節點或者3節點，2節點與3節點在紅黑樹中的等價形式，如下圖所示

顯然，無論是哪種情況，根節點都是黑色的。
性質3：每個葉子節點（NIL）是黑色。
這里的葉子節點不是指左右子樹為空的那個葉子節點，而是指節點不存在子節點或者為空節點被稱作葉子節點。在性質2中我們討論的根節點是黑色的都是討論根節點不為空的情況，若紅黑樹是一個空樹，那么根節點自然也是空的葉子節點，這時候葉子節點便必然是黑色的。
性質4：每個紅色結點的兩個子結點一定都是黑色。
還是從2-3樹的角度來理解，紅色節點對應2-3樹中3節點左側的元素，那么它的子節點要么是2節點，要么是3節點。無論是2節點還是3節點對應的節點顏色都是黑色的，這在性質2時已經討論了。
性質5：任意一結點到每個葉子結點的路徑都包含數量相同的黑結點。
性質5應該是紅黑樹最重要的一條性質了。2-3樹是一顆絕對平衡的樹，即2-3樹中任意一個節點出發，到達葉子節點后所經過的節點數都是一樣的。那么對應到紅黑樹呢？2-3樹中2節點對應到紅黑樹便是一個黑色的節點，而3節點對應到紅黑樹是一個紅色節點和一個黑色節點。所以，無論是2節點還是3節點，在紅黑樹中都會對應一個黑色節點。那么2-3樹中的絕對平衡，在紅黑樹中自然就是任意一結點到每個葉子結點的路徑都包含數量相同的黑結點了。
相信大家現在已經對紅黑樹的五條性質有了更加深刻的體會了。那么我們再看下紅黑樹維持平衡的三種操作，即變色、左旋、右旋怎么理解呢？
首先看一下變色，以下圖為例，

在2-3樹中插入節點3后，便不再滿足2-3樹的定義，需要進行分解，將元素2抽出作為1和3的父節點，然后2繼續向上融合。
對應到紅黑樹中就是，首先插入節點3，在紅黑樹中新插入的節點默認為紅色，然后不滿足定義，所以需要進行分解，分解后各個節點都為2節點，所以變為黑色。而2節點需要繼續向上融合，故要變成紅色。
接著看一下 右旋轉，以下圖為例，

插入元素1后，進行右旋轉操作，首先把2節點與3節點斷開連接，同時把2與2的右子樹斷開連接，然后把2的右子樹連接至3的左子樹位置，不會違背二分搜索樹的性質，然后再把3連接至2的右子樹位置。最后還要改變對應節點的顏色，即把2節點的顏色改為原來3節點的黑色，把3節點的顏色改為原來2節點的紅色。
接著看一下 左旋轉，與右旋轉類似，以下圖為例，

插入元素3后，進行左旋轉操作，首先把2節點與3節點斷開連接，同時把3與3的左子樹斷開連接，然后把3的左子樹連接至2的右子樹位置，不會違背二分搜索樹的性質，然后再把2連接至3的左子樹位置。最后還要改變對應節點的顏色，即把2節點的顏色改為原來3節點的紅色，把3節點的顏色改為原來2節點的黑色。

關于“什么是紅黑樹”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識，可以關注億速云行業資訊頻道，小編每天都會為大家更新不同的知識點。

向AI問一下細節

91超碰碰碰碰久久久久久综合_超碰av人澡人澡人澡人澡人掠_国产黄大片在线观看画质优化_txt小说免费全本

什么是紅黑樹

為什么要有紅黑樹

從2-3樹來看紅黑樹

再看紅黑樹

猜你喜歡

91超碰碰碰碰久久久久久综合_超碰av人澡人澡人澡人澡人掠_国产黄大片在线观看画质优化_txt小说免费全本

什么是紅黑樹

為什么要有紅黑樹

從2-3樹來看紅黑樹

再看紅黑樹

猜你喜歡

最新資訊

相關推薦

相關標簽