您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“HashMap紅黑樹樹化過程是怎樣的”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“HashMap紅黑樹樹化過程是怎樣的”吧!
HashMap是Java程序員使用頻率最高的用于映射(鍵值對)處理的數據類型。隨著JDK(Java Developmet Kit)版本的更新,JDK1.8對HashMap底層的實現進行了優化,例如引入紅黑樹的數據結構和擴容的優化等。
一個節點標記為紅色或者黑色。 根是黑色的。 如果一個節點是紅色的,那么它的子節點必須是黑色的(這就是為什么叫紅黑樹)。 一個節點到到一個null引用的每一條路徑必須包含相同數目的黑色節點(所以紅色節點不影響)。 其實RB Tree和著名的AVL Tree有很多相同的地方,困難的地方都在于將一個新項插入到樹中。了解AVL Tree的朋友應該都知道為了維持樹的高度必須在插入一個新的項后必須在樹的結構上進行改變,這里主要是通過旋轉,當然在RB Tree中原理也是如此。
旋轉的方向:

變換過程:

互相關聯:

單向關聯:

代表紅色的節點:

代表黑色的節點:

代表一個不會破壞紅黑樹結構的部分,可能是節點,或者是一個子樹,總之不會破環當前樹的結構。這個部分會由于旋轉而連接到其他的節點后面,我們可以理解成由于重力原因它掉到了下面的節點上:


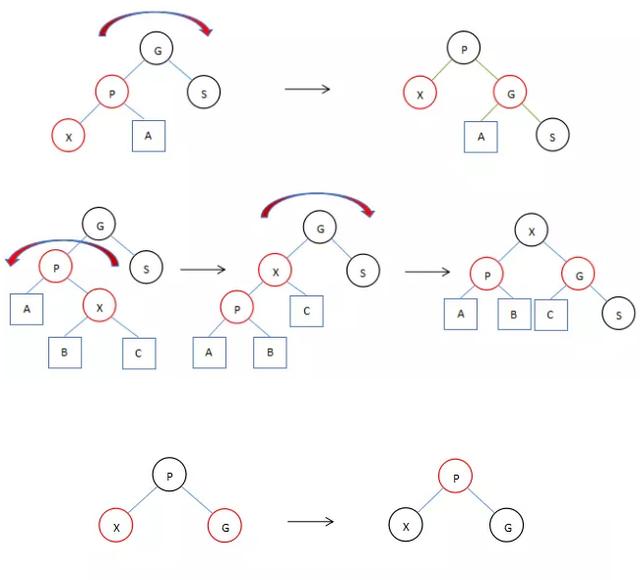
單旋轉變換。
雙旋轉變換(需要兩次反方向的單旋轉)。
當遇到兩個子幾點都為紅色的話執行顏色變換,因為插入 是紅色的會產生沖突。如果根節點兩邊的子節點都是紅色,兩個葉子節點變成黑色,根節點變成紅色,然后再將根節點變成黑色。
上面的圖中描述了紅黑樹中三種典型的變換,其實前兩種變換這正是AVL Tree中的兩種典型的變換。
4.1 為什么要進行旋轉?
由于P和X節點都為紅色節點這破環了紅節點下面的節點必須為黑色節點的規則。
4.2 新加入的節點總是紅色的,這是為什么呢?
因為被插入前的樹結構是構建好的,一但我們進行添加黑色的節點,無論添加在哪里都會破壞原有路徑上的黑色節點的數量平等關系,所以插入紅色節點是正確的選擇。
4.3 為什么要進行顏色變換?
正如第一種旋轉新加入的節點X破壞了紅黑樹的結構不得不進行旋轉,后面的就是旋轉后的結果,旋轉后形成新的結構,此時我們發現兩個子節點都是紅色的所以執行第三個變換特性,顏色變換,因為如果子節點是紅色的那么我們在添加的時候只能添加黑色的節點,然而添加任何黑色葉子節點都會破壞樹的第四條性質,所以要對其進行變換。當進行變換后葉子節點是紅色的而且我們默認添加的葉子節點是紅色的,所以添加到黑色節點后并不會破壞樹的第四條結構,所以這種變換很有用。
第二種雙變換中在樹的內部怎么出現的紅色的節點? 正是由于上面的顏色變換導致新顏色變換后的節點與他的父節點產生了顏色沖突。
與AVL樹相比? 比AVL樹相比優點是不用在節點類中保存一個節點高度這個變量,節省了內存。
而且紅黑樹一般不是以遞歸方式實現的而是以循環的形式實現。
一般的操作在最壞情形下花費O(logN)時間。
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K, V>[] tab; Node<K, V> p; int n, i; if ((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length; if ((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null); else { Node<K, V> e; K k; if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) e = p; else if (p instanceof TreeNode) // 如果當前的bucket里面已經是紅黑樹的話,執行紅黑樹的添加操作 e = ((TreeNode<K, V>) p).putTreeVal(this, tab, hash, key, value); else { for (int binCount = 0;; ++binCount) { if ((e = p.next) == null) { p.next = newNode(hash, key, value, null); // TREEIFY_THRESHOLD = 8,判斷如果當前bucket的位置鏈表長度大于8的話就將此鏈表變成紅黑樹。 if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st treeifyBin(tab, hash); break; } if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) break; p = e; } } if (e != null) { // existing mapping for key V oldValue = e.value; if (!onlyIfAbsent || oldValue == null) e.value = value; afterNodeAccess(e); return oldValue; } } ++modCount; if (++size > threshold) resize(); afterNodeInsertion(evict); return null; }上面的方法通過hash計算插入的項的槽位,如果有是一樣的key則根據設置的參數是否執行覆蓋,如果相應槽位空的話直接插入,如果對應的槽位有項則判斷是紅黑樹結構還是鏈表結構的槽位,鏈表的話則順著鏈表尋找如果找到一樣的key則根據參數選擇覆蓋,沒有找到則鏈接在鏈表最后面,鏈表項的數目大于8則對其進行樹化,如果是紅黑樹結構則按照樹的添加方式添加項。
讓我們看一下treeifyBin這個方法。
final void treeifyBin(Node<K, V>[] tab, int hash) { int n, index; Node<K, V> e; if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) // resize()方法這里不過多介紹,感興趣的可以去看上面的鏈接。 resize(); // 通過hash求出bucket的位置。 else if ((e = tab[index = (n - 1) & hash]) != null) { TreeNode<K, V> hd = null, tl = null; do { // 將每個節點包裝成TreeNode。 TreeNode<K, V> p = replacementTreeNode(e, null); if (tl == null) hd = p; else { // 將所有TreeNode連接在一起此時只是鏈表結構。 p.prev = tl; tl.next = p; } tl = p; } while ((e = e.next) != null); if ((tab[index] = hd) != null) // 對TreeNode鏈表進行樹化。 hd.treeify(tab); } }找個方法所做的事情就是將剛才九個項以鏈表的方式連接在一起,然后通過它構建紅黑樹。
看代碼之前我們先了解一下TreeNode
static final class TreeNode<K, V> extends LinkedHashMap.Entry<K, V> { TreeNode<K, V> parent; // red-black tree links TreeNode<K, V> left; TreeNode<K, V> right; TreeNode<K, V> prev; // needed to unlink next upon deletion boolean red; TreeNode(int hash, K key, V val, Node<K, V> next) { super(hash, key, val, next); } final void treeify(Node<K,V>[] tab) { // ...... } static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root, TreeNode<K,V> x) { // ...... } static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root, TreeNode<K,V> p) { // ...... } static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root, TreeNode<K,V> p) { // ...... } // ......其余方法省略 }可以看出出真正的維護紅黑樹結構的方法并沒有在HashMap中,全部都在TreeNode類內部。
我們看一下treeify代碼
final void treeify(Node<K, V>[] tab) { TreeNode<K, V> root = null; // 以for循環的方式遍歷剛才我們創建的鏈表。 for (TreeNode<K, V> x = this, next; x != null; x = next) { // next向前推進。 next = (TreeNode<K, V>) x.next; x.left = x.right = null; // 為樹根節點賦值。 if (root == null) { x.parent = null; x.red = false; root = x; } else { // x即為當前訪問鏈表中的項。 K k = x.key; int h = x.hash; Class<?> kc = null; // 此時紅黑樹已經有了根節點,上面獲取了當前加入紅黑樹的項的key和hash值進入核心循環。 // 這里從root開始,是以一個自頂向下的方式遍歷添加。 // for循環沒有控制條件,由代碼內break跳出循環。 for (TreeNode<K, V> p = root;;) { // dir:directory,比較添加項與當前樹中訪問節點的hash值判斷加入項的路徑,-1為左子樹,+1為右子樹。 // ph:parent hash。 int dir, ph; K pk = p.key; if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) dir = tieBreakOrder(k, pk); // xp:x parent。 TreeNode<K, V> xp = p; // 找到符合x添加條件的節點。 if ((p = (dir <= 0) ? p.left : p.right) == null) { x.parent = xp; // 如果xp的hash值大于x的hash值,將x添加在xp的左邊。 if (dir <= 0) xp.left = x; // 反之添加在xp的右邊。 else xp.right = x; // 維護添加后紅黑樹的紅黑結構。 root = balanceInsertion(root, x); // 跳出循環當前鏈表中的項成功的添加到了紅黑樹中。 break; } } } } // Ensures that the given root is the first node of its bin,自己翻譯一下。 moveRootToFront(tab, root); }第一次循環會將鏈表中的首節點作為紅黑樹的根,而后的循環會將鏈表中的的項通過比較hash值然后連接到相應樹節點的左邊或者右邊,插入可能會破壞樹的結構所以接著執行balanceInsertion。
我們看balanceInsertion
static <K, V> TreeNode<K, V> balanceInsertion(TreeNode<K, V> root, TreeNode<K, V> x) { // 正如開頭所說,新加入樹節點默認都是紅色的,不會破壞樹的結構。 x.red = true; // 這些變量名不是作者隨便定義的都是有意義的。 // xp:x parent,代表x的父節點。 // xpp:x parent parent,代表x的祖父節點 // xppl:x parent parent left,代表x的祖父的左節點。 // xppr:x parent parent right,代表x的祖父的右節點。 for (TreeNode<K, V> xp, xpp, xppl, xppr;;) { // 如果x的父節點為null說明只有一個節點,該節點為根節點,根節點為黑色,red = false。 if ((xp = x.parent) == null) { x.red = false; return x; } // 進入else說明不是根節點。 // 如果父節點是黑色,那么大吉大利(今晚吃雞),紅色的x節點可以直接添加到黑色節點后面,返回根就行了不需要任何多余的操作。 // 如果父節點是紅色的,但祖父節點為空的話也可以直接返回根此時父節點就是根節點,因為根必須是黑色的,添加在后面沒有任何問題。 else if (!xp.red || (xpp = xp.parent) == null) return root; // 一旦我們進入到這里就說明了兩件是情 // 1.x的父節點xp是紅色的,這樣就遇到兩個紅色節點相連的問題,所以必須經過旋轉變換。 // 2.x的祖父節點xpp不為空。 // 判斷如果父節點是否是祖父節點的左節點 if (xp == (xppl = xpp.left)) { // 父節點xp是祖父的左節點xppr // 判斷祖父節點的右節點不為空并且是否是紅色的 // 此時xpp的左右節點都是紅的,所以直接進行上面所說的第三種變換,將兩個子節點變成黑色,將xpp變成紅色,然后將紅色節點x順利的添加到了xp的后面。 // 這里大家有疑問為什么將x = xpp? // 這是由于將xpp變成紅色以后可能與xpp的父節點發生兩個相連紅色節點的沖突,這就又構成了第二種旋轉變換,所以必須從底向上的進行變換,直到根。 // 所以令x = xpp,然后進行下下一層循環,接著往上走。 if ((xppr = xpp.right) != null && xppr.red) { xppr.red = false; xp.red = false; xpp.red = true; x = xpp; } // 進入到這個else里面說明。 // 父節點xp是祖父的左節點xppr。 // 祖父節點xpp的右節點xppr是黑色節點或者為空,默認規定空節點也是黑色的。 // 下面要判斷x是xp的左節點還是右節點。 else { // x是xp的右節點,此時的結構是:xpp左->xp右->x。這明顯是第二中變換需要進行兩次旋轉,這里先進行一次旋轉。 // 下面是第一次旋轉。 if (x == xp.right) { root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } // 針對本身就是xpp左->xp左->x的結構或者由于上面的旋轉造成的這種結構進行一次旋轉。 if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateRight(root, xpp); } } } } // 這里的分析方式和前面的相對稱只不過全部在右測不再重復分析。 else { if (xppl != null && xppl.red) { xppl.red = false; xp.red = false; xpp.red = true; x = xpp; } else { if (x == xp.left) { root = rotateRight(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateLeft(root, xpp); } } } } } }如果您的聯想能力很強的話估計到這里應該已經理解這集中變換的主要的關系。
下面簡述一下前面的兩種種幸運的情況
x本身為根節點返回x。 x的父節點為黑色或者x的父節點是根節點直接返回不需要變換。 如若上述兩個條件不滿足的話,就要進行變換了,允許我再貼一點代碼......沒有代碼分析起來很困難。
if (xp == (xppl = xpp.left)) { if ((xppr = xpp.right) != null && xppr.red) { xppr.red = false; xp.red = false; xpp.red = true; x = xpp; } }這里是一個典型的一個黑色節點的兩個子節點都是紅色的所以要進行顏色變換,因為插入的都是紅色節點,當檢測到祖父節點的左右子節點都是紅色的時候兩個紅色就產生了沖突,所以先將節點進行這種顏色變換,將祖父節點變成紅色,然后將祖父的兩個子節點變成黑色,這樣我們插入的紅色節點就不會違背紅黑樹的規則了。

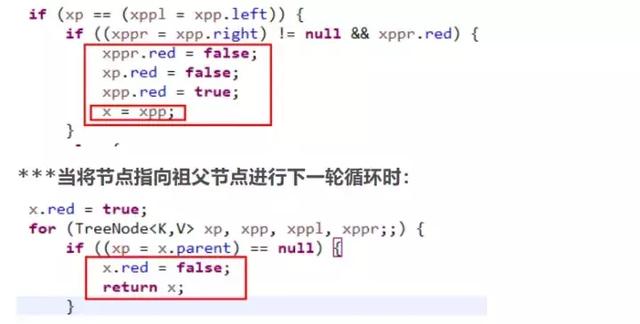
這里有人會有疑問,如果祖父節點是根節點呢,那樣的話祖父節點也會變成黑色,因為每次循環進行插入平衡的操作當進行這種顏色變換之后都會將插入節點的引用指向祖父節點,當進行下一輪循環的時候會優先檢測當前節點是否是根節點,如果是根節點那就將顏色變成黑色,下面看圖:
當將節點指向祖父節點進行下一輪循環時:
// 一旦我們進入到這里就說明了兩件是情 // 1.x的父節點xp是紅色的,這樣就遇到兩個紅色節點相連的問題,所以必須經過旋轉變換。 // 2.x的祖父節點xpp不為空。 // 判斷如果父節點是否是祖父節點的左節點 if (xp == (xppl = xpp.left)) { if ((xppr = xpp.right) != null && xppr.red) {// ...... } // 進入到這個else里面說明。 // 父節點xp是祖父的左節點xppr。 // 祖父節點xpp的右節點xppr是黑色節點或者為空,默認規定空節點也是黑色的。 // 下面要判斷x是xp的左節點還是右節點。 else { // x是xp的右節點,此時的結構是:xpp左->xp右->x。這明顯是第二中變換需要進行兩次旋轉,這里先進行一次旋轉。 // 下面是第一次旋轉。 if (x == xp.right) { root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } // 針對本身就是xpp左->xp左->x的結構或者由于上面的旋轉造成的這種結構進行一次旋轉。 if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateRight(root, xpp); } } } }顏色變換完成后進入下面的else塊
我們已知xp是xpp的左節點,首先判斷了x是xp的左節點還是右節點,如果是右節點的話構成了下面的結構。
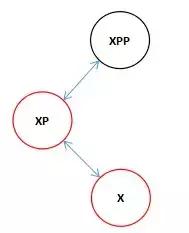
這中結構需要進行雙旋轉,首先先進行一次向左旋轉。
7.1 左旋轉
1 static <K, V> TreeNode<K, V> rotateLeft(TreeNode<K, V> root, TreeNode<K, V> p) 2 { 3 // r:right,右節點。 4 // pp:parent parent,父節點的父節點。 5 // rl:right left,右節點的左節點。 6 TreeNode<K, V> r, pp, rl; 7 if (p != null && (r = p.right) != null) 8 { 9 if ((rl = p.right = r.left) != null) 10 rl.parent = p; 11 if ((pp = r.parent = p.parent) == null) 12 (root = r).red = false; 13 else if (pp.left == p) 14 pp.left = r; 15 else 16 pp.right = r; 17 r.left = p; 18 p.parent = r; 19 } 20 return root; 21 }1.剛進入方法時,狀態如下圖。(RL可能是空的)
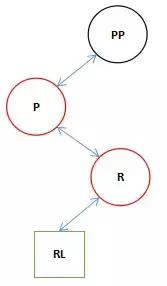
2.進入了if塊后執行到第10行后。
9 if ((rl = p.right = r.left) != null) 10 rl.parent = p;
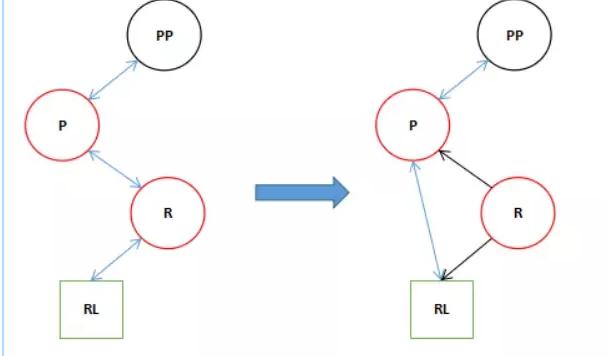
此時如果9行的條件符合的話執行10行RL指向P,如果RL為null的話,P的右節點指向null。
3.接著看11和12行代碼。
11 if ((pp = r.parent = p.parent) == null) 12 (root = r).red = false;
首先我們看11行if里面的賦值語句所造成的影響。
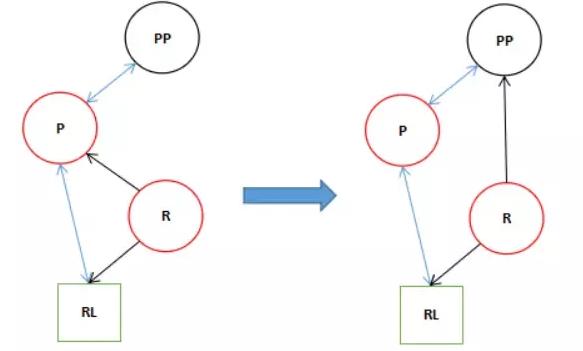
在if里面的表達式不管符不符合條件()內的內容都會執行。
如果符合條件的話會執行12行的代碼,變成了下面的結果。
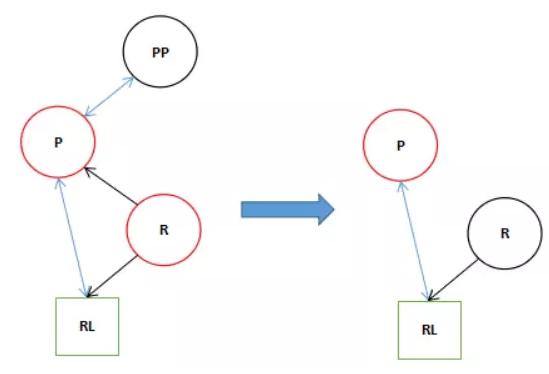
由于PP為空所以只剩下這三個。
4.如果11行的條件為假的話,執行完11行()內的表達式后執行13行
13 else if (pp.left == p) 14 pp.left = r;
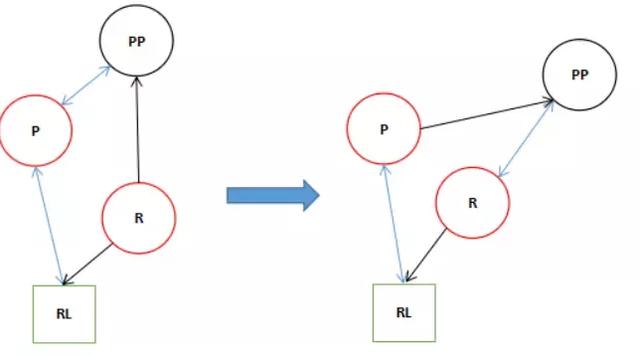
滿足條件的話R和PP互相關聯。
5.由于進入了13和14行所以不進入15和16行的else語句。
15 else 16 pp.right = r;
6.看17和18行。
17 r.left = p; 18 p.parent = r;
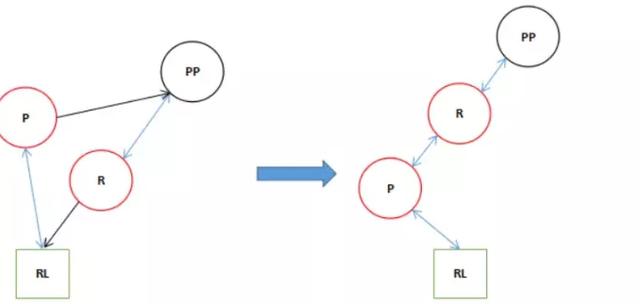
最終執行完了一個旋轉變成了我們開始說的第一種旋轉的形式,這個結構還需要向右旋轉一次。
if (x == xp.right) { root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } xpp = (xp = x.parent) == null ? null : xp.parent;執行完上面的代碼,旋轉后調整x,xp,和xpp的關系得到下圖。
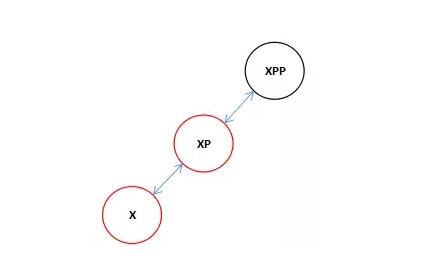
7.2 右旋轉
if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateLeft(root, xpp); } }1.首先讓XP變成黑色。
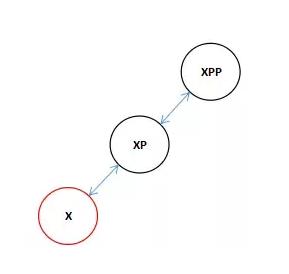
2.如果XPP不為空的話變成紅色。
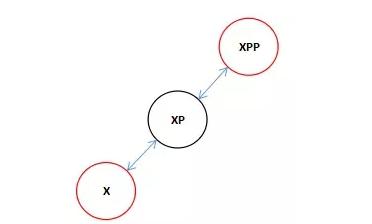
由于我們在rotateLeft(root, xpp),傳進來的是XXP所以下面的的旋轉中實際上就是對XP和XXP執行了一次與上面的方向相反其他完全相同的旋轉。
接著我們看向右旋轉的代碼
static <K, V> TreeNode<K, V> rotateRight(TreeNode<K, V> root, TreeNode<K, V> p) { // l:left,左節點。 // pp:parent parent,父節點的父節點。 // lr:left right,左節點的右節點。 TreeNode<K, V> l, pp, lr; if (p != null && (l = p.left) != null) { if ((lr = p.left = l.right) != null) lr.parent = p; if ((pp = l.parent = p.parent) == null) (root = l).red = false; else if (pp.right == p) pp.right = l; else pp.left = l; l.right = p; p.parent = l; } return root; }3.剛進來的時候結構是這個樣子。
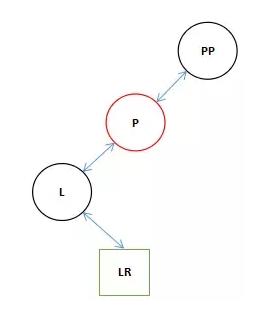
在這里的P就是剛才傳進來的XPP。
4.這里我們認為LR是存在的,其實這個不影響主要的旋轉,為空就指向null唄,直接執行完9和10行。
9 if ((lr = p.left = l.right) != null) 0 lr.parent = p;
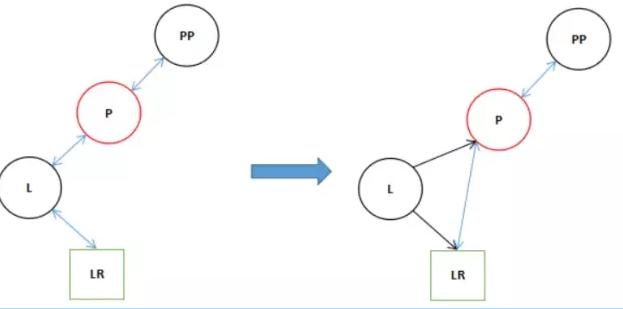
5.在這里我們假使PP是存在的,直接執行完11的表達式不再執行12行。(不再分析不存在的情況)。
11 if ((pp = l.parent = p.parent) == null) 12 (root = l).red = false;
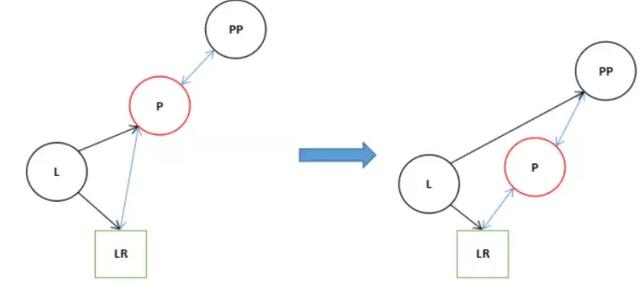
6.由于11行的條件不符合,現在直接執行13行的表達式,不符合執行15行else,執行16行。
15 else 16 pp.left = l;
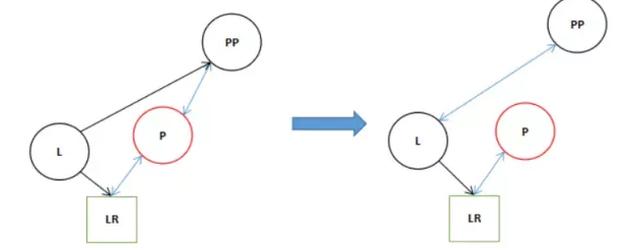
7.最后執行層17和18行。
17 l.right = p; 18 p.parent = l;
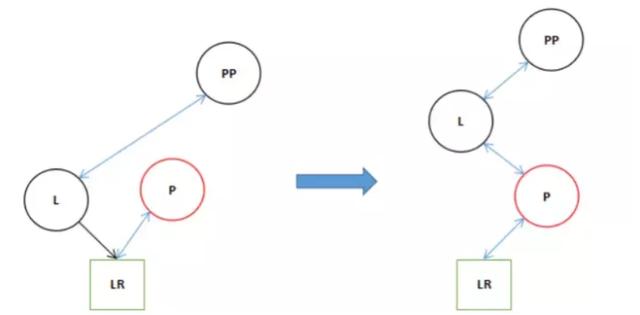
最終完成兩次的旋轉。
大家可能覺得和剛才接不上其實是這樣的,剛才在右旋轉前的時候的圖像是這個樣的。
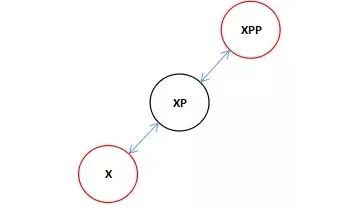
因為我們傳進來的是XPP,所以結合上一次的向左旋轉我們在向右旋轉的時候看到全圖應該是這個樣子的。(注:XPPP可能是XPP的左父節點也可能是右父節點這里不影響,而且可以是任意顏色)
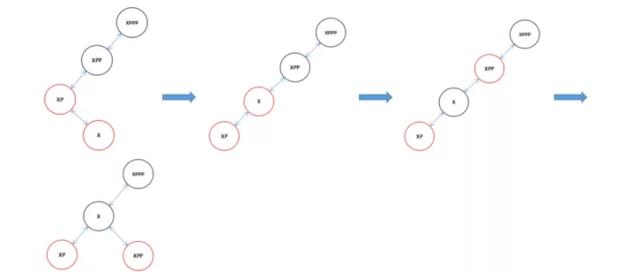
現在知道為什么XPPP可以是任意顏色的了吧,因為旋轉過后X是黑色的即便XPPP是紅色,此時我們又可以對兩個紅色的子節點進行顏色變換了,變換后X和XPPP有發生了顏色沖突,接著進行旋轉直到根。
static <K, V> TreeNode<K, V> balanceInsertion(TreeNode<K, V> root, TreeNode<K, V> x) { x.red = true; for (TreeNode<K, V> xp, xpp, xppl, xppr;;) { if ((xp = x.parent) == null) { x.red = false; return x; } else if (!xp.red || (xpp = xp.parent) == null) return root; if (xp == (xppl = xpp.left)) { // 插入位置父節點在祖父節點的左邊。 } else { // 插入位置父節點在祖父節點的右邊。 } } }我們值分析了插入位置父節點在祖父節點的左邊的情況,并沒有分析另外一面的對稱情況,其實是一樣的因為調用的都是相同的方法。
到此,相信大家對“HashMap紅黑樹樹化過程是怎樣的”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。