您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
概述:R-B Tree,又稱為“紅黑樹”。本文參考了《算法導論》中紅黑樹相關知識,加之自己的解,然后以圖文的形式對紅黑樹進行說明。本文的主要內容包括:紅黑樹的特性,紅黑樹的時間復雜度和它的證明,紅黑樹的左旋、右旋、插入等操作。
1 R-B Tree簡介
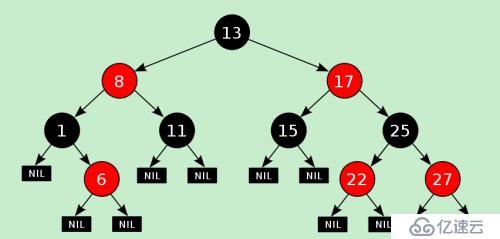
R-B Tree,全稱是Red-Black Tree,又稱為“紅黑樹”,它一種特殊的二叉查找樹。紅黑樹的每個節點上都有存儲位表示節點的顏色,可以是紅(Red)或黑(Black)。
紅黑樹的特性:
(1)每個節點或者是黑色,或者是紅色。
(2)根節點是黑色。
(3)每個葉子節點(NIL)是黑色。 [注意:這里葉子節點,是指為空(NIL或NULL)的葉子節點!]
(4)如果一個節點是紅色的,則它的子節點必須是黑色的。
(5)從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。
2 R-B Tree時間復雜度
紅黑樹的時間復雜度為: O(lgn)
定理:一棵含有n個節點的紅黑樹的高度至多為2log(n+1).
3 R-B Tree基本操作
R-B Tree的基本操作是添加、刪除。 添加和刪除操作,都會用到兩個基本的方法:左旋 和 右旋,統稱為旋轉。旋轉是為了保持紅黑樹的特性而提供的輔助方法,因為當我們進行添加、刪除節點時,可能改變紅黑樹的特性(例如,刪除一個黑色節點之后,就不滿足“從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點”這個特性);這里,我們就需要旋轉方法的輔助來讓樹保持紅黑樹的特性。
向一顆含有n個節點的紅黑樹中插入一個節點,可以在時間O(lgn)內完成。
將節點z插入紅黑樹T內。需要執行的操作依次時:首先,將T當作一顆二叉樹,將z插入;然后,將z著色為紅色;最后,通過RB-INSERT-FIXUP來對節點重新著色并旋轉,以此來保證刪除節點后的樹仍然是一顆紅黑樹。
(01) 將T當作一顆二叉樹,將z插入。
因為紅黑樹本身就是一顆二叉樹,所以,我們可以根據二叉樹的性質將z插入。
(02) 將z著色為紅色。
在介紹為什么將則著色為紅色之前,我們重新溫習一下紅黑樹的特性:
(1)每個節點或者是黑色,或者是紅色。
(2)根節點是黑色。
(3)每個葉子節點(NIL)是黑色。 [注意:這里葉子節點,是指為空(NIL或NULL)的葉子節點!]
(4)如果一個節點是紅色的,則它的子節點必須是黑色的。
(5)從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。
將插入的節點著色為紅色,不會違背“特性(5)”;而若將插入的節點著色為黑色,會違背該特性。
(03) 通過RB-INSERT-FIXUP來對節點重新著色并旋轉。
因為(02)中插入一個紅色節點之后,雖然沒有違背“特性(5)”,但是卻可能違背了其它特性(例如,若被插入節點的父節點也是紅色;插入后,則違背了“特性(4)”)。我們需要通過RB-INSERT-FIXUP進行節點顏色的調整以及旋轉等工作,讓樹仍然是一顆紅黑樹。
總的來說:當節點z被著色為紅色節點,并插入二叉樹時,有三種情況。
情況一:被插入的節點是根節點。
直接把此節點涂為黑色。
情況二:被插入的節點的父節點是黑色。
什么也不需要做。節點被插入后,仍然是紅黑樹。
情況三:被插入的節點的父節點是紅色。
那么,該情況與紅黑樹的“特性(5)”相沖突。情況三包含了“Case 1”、“Case 2” 和“Case 3”三種情況,情況三的目的是恢復紅黑樹的特性,它的處理思想是:將紅色的節點移到根節點;然后,將根節點設為黑色。下面介紹情況三的三種情況。
Case 1 現象說明:當前節點的父節點是紅色,且當前節點的祖父節點的另一個子節點(叔叔節點)也是紅色。
Case 1 處理策略:
(01) 將“父節點”設為黑色。
(02) 將“叔叔節點”設為黑色。
(03) 將“祖父節點”設為“紅色”。
(04) 將“祖父節點”設為“當前節點”(紅色節點);即,之后繼續對“當前節點”進行操作。
Case 2 現象說明:當前節點的父節點是紅色,叔叔節點是黑色,且當前節點是其父節點的右孩子
Case 2 處理策略:
(01) 將“父節點”作為“新的當前節點”。
(02) 以“新的當前節點”為支點進行左旋。
Case 3:叔叔是黑色,當前節點是做孩子
Case 3:叔叔是黑色,且當前節點是左孩子
Case 3 現象說明:當前節點的父節點是紅色,叔叔節點是黑色,且當前節點是其父節點的左孩子
Case 3 處理策略:
(01) 將“父節點”設為“黑色”。
(02) 將“祖父節點”設為“紅色”。
(03) 以“祖父節點”為支點進行右旋。
#include<iostream>
using namespace std;
enum Color
{
BLACK,
RED
};
template<class K,class V>
struct RBTreeNode
{
RBTreeNode(const K& key,const V&value,const Color col = RED)
:_left(NULL)
,_right(NULL)
,_parent(NULL)
,_col(col)
,_key(key)
,_value(value)
{}
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
Color _col;
K _key;
V _value;
};
template<class K,class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
RBTree()
:_root(NULL)
{}
bool Insert(const K& key, const V& value)
{
if (_root == NULL)
{
_root = new Node(key, value, BLACK);
return true;
}
Node* parent = NULL;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
break;
}
}
cur = new Node(key, value, RED);
if (parent->_key <key)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
//調色
while (cur != _root && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
//當叔叔節點為黑色,且S為F的右孩子,處理步驟;1 以父節點進行左旋 2將父節點變黑祖父節點變紅,3然后進行右旋
else
{
if (cur == parent->_right)
{
RotateL(parent);
swap(cur, parent);
}
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
}
else //往右子樹插
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)
{
RotateR(parent);
swap(cur, parent);
}
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
}
}
_root->_col = BLACK;
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
protected:
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if(subRL)
{
subRL->_parent = parent;
}
subR->_left = parent;
subR->_parent = parent->_parent;
parent = subR;
if (parent->_parent == NULL)
{
_root = parent;
}
else
{
if (parent->_key < parent->_parent->_key)
{
parent->_parent->_left = parent;
}
else
{
parent->_parent->_right = parent;
}
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if(subLR)
{
subLR->_parent = parent;
}
subL->_right = parent;
subL->_parent = parent->_parent;
parent->_parent = subL;
parent = subL;
if (parent->_parent == NULL)
{
_root = parent;
}
else
{
if (parent->_key < parent->_parent->_key)
{
parent->_parent->_left = parent;
}
else
{
parent->_parent->_right = parent;
}
}
}
void _InOrder(Node*& root)
{
if (root == NULL)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
protected:
Node* _root;
};
void TestRBTree()
{
RBTree<int, int> t1;
int a[10] = { 5, 2, 9, 6, 7, 3, 40, 1, 8 };
for (size_t i = 0; i < sizeof(a) / sizeof(a[0]); ++i)
{
t1.Insert(a[i], i);
t1.InOrder();
}
cout << "IsBalanceTree:" << t1.IsBalanceTree() << endl;
}
int main()
{
TestRBTree();
system("pause");
return 0;
}4 運行結果
5 紅黑樹的應用
紅黑樹的應用比較廣泛,主要是用它來存儲有序的數據,它的時間復雜度是O(lgn),效率非常之高。
例如,Java中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虛擬內存的管理,都是通過紅黑樹去實現的。
這里大致介紹下,紅黑樹和AVL樹的差異。AVL樹也是特殊的二叉樹,它的特性是“任何節點的左右子樹的高度之差不超過1”。基本上,用到紅黑樹的地方都可以用AVL樹(自平衡二叉查找樹)去替換。但是一般情況下,在執行添加、刪除節點時,AVL樹比紅黑樹執行的操作更多一些,效率更低一些;而且紅黑樹也是相對平衡的二叉樹(從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點)。因此,紅黑樹的效率會高更一點。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。