您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
RNN背后的數學原理是什么,針對這個問題,這篇文章詳細介紹了相對應的分析和解答,希望可以幫助更多想解決這個問題的小伙伴找到更簡單易行的方法。
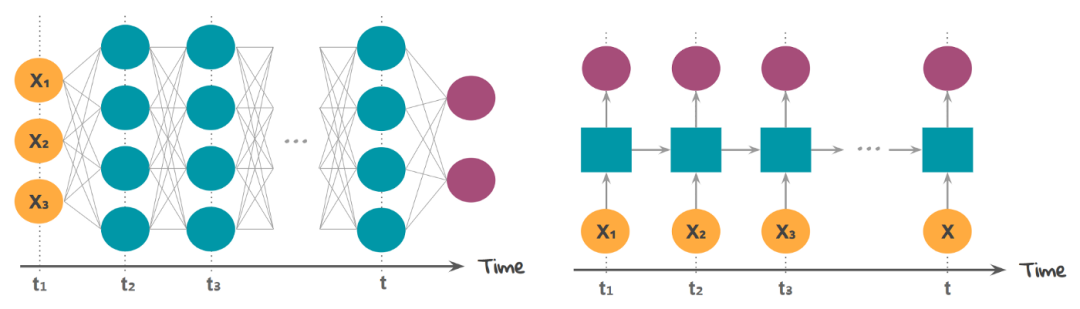

這篇文章的目的是對循環神經網絡的功能、結構提供一個直觀的認識。
一個神經網絡通常取自變量
但如果數據的順序很重要呢?想象一下,如果所有自變量的順序都很重要呢?
讓我來直觀地解釋一下吧。

只要假設每個螞蟻是一個獨立變量,如果一個螞蟻朝著不同的方向前進,對其他螞蟻來說都沒關系,對吧?但是,如果螞蟻的順序很重要怎么辦?

此時,如果一只螞蟻錯過或者離開了群體,它將會影響到后面的螞蟻。
那么,在機器學習空間中,哪些數據的順序是重要的呢?
那么 RNN 是如何解決整體順序很重要的數據呢?我們用自然文本數據為例來解釋 RNN。
假設我正在對一部電影的用戶評論進行情感分析。
從這部電影好(This movie is good) — 正面的,再到這部電影差(This movie is bad) — 負面的。
我們可以通過使用簡單的詞匯袋模型對它們進行分類,我們可以預測(正面的或負面的),但是等等。
如果影評是這部電影不好(This movie is not good),怎么辦?
BOW 模型可能會說這是一個積極的信號,但實際上并非如此。而 RNN 理解它,并預測它是消極的信息。
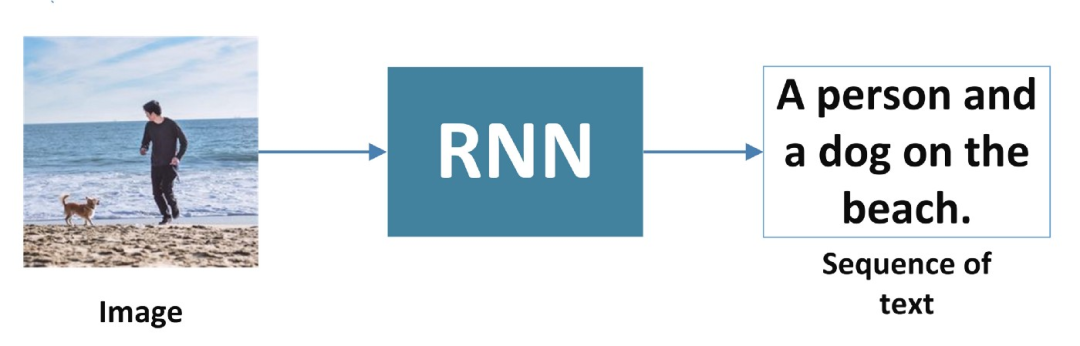
1、一對多
RNN 接受一個輸入,比如一張圖像,并生成一個單詞序列。
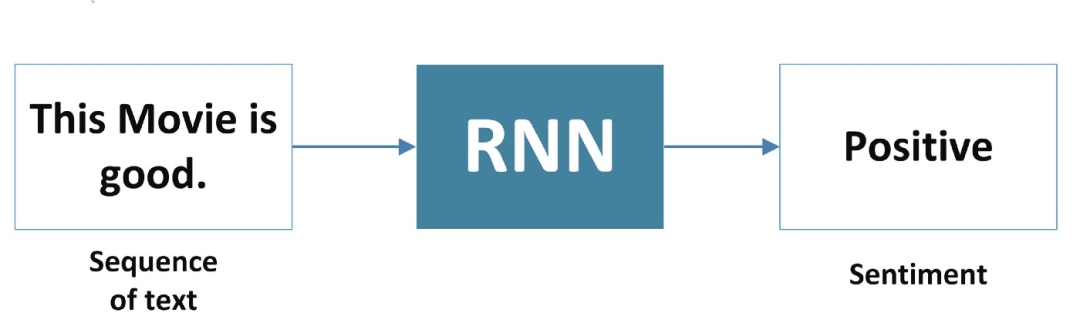
2、多對一
RNN 接受一個單詞序列作為輸入,并生成一個輸出。
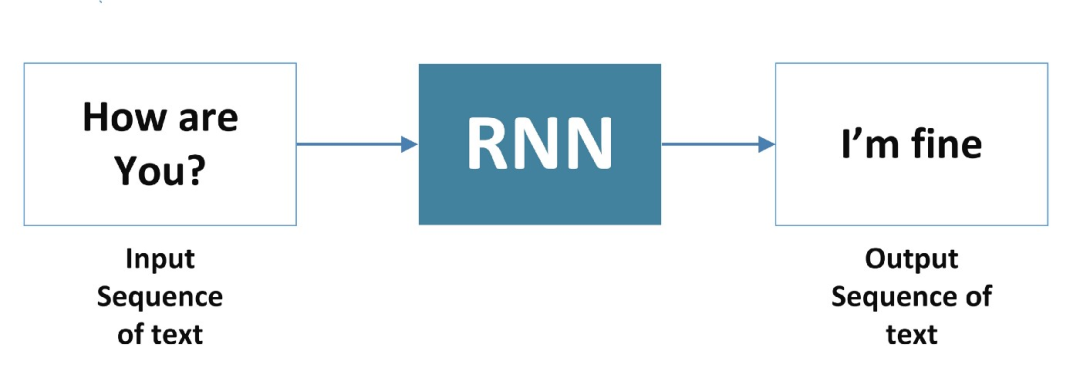
3、多對多
接下來,我們正專注于第二種模式多對一。RNN 的輸入被視為時間步長。
示例: 輸入(X) = [" this ", " movie ", " is ", " good "]
this 的時間戳是 x(0),movie 的是 x(1),is 的是 x(2),good 的是 x(3)。
下面讓我們深入到 RNN 的數學世界。
首先,讓我們了解 RNN 單元格包含什么!我希望并且假設大家知道前饋神經網絡,FFNN 的概括,
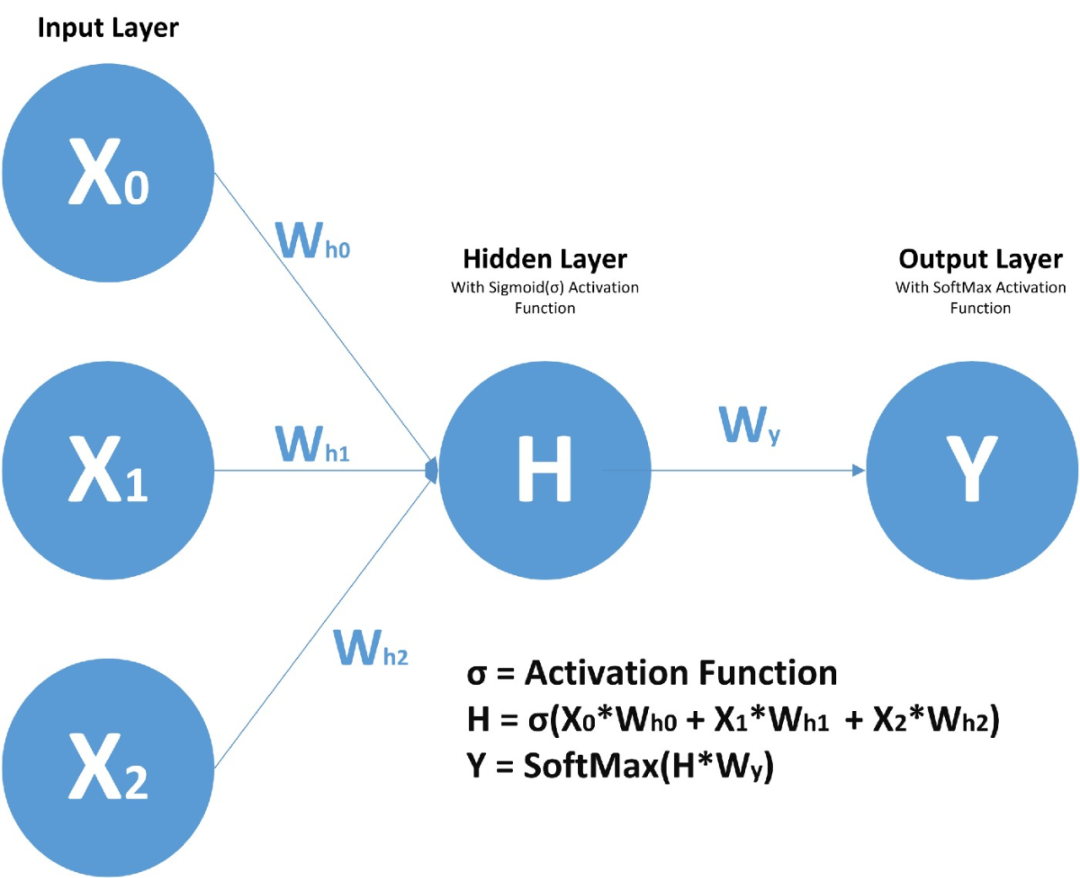
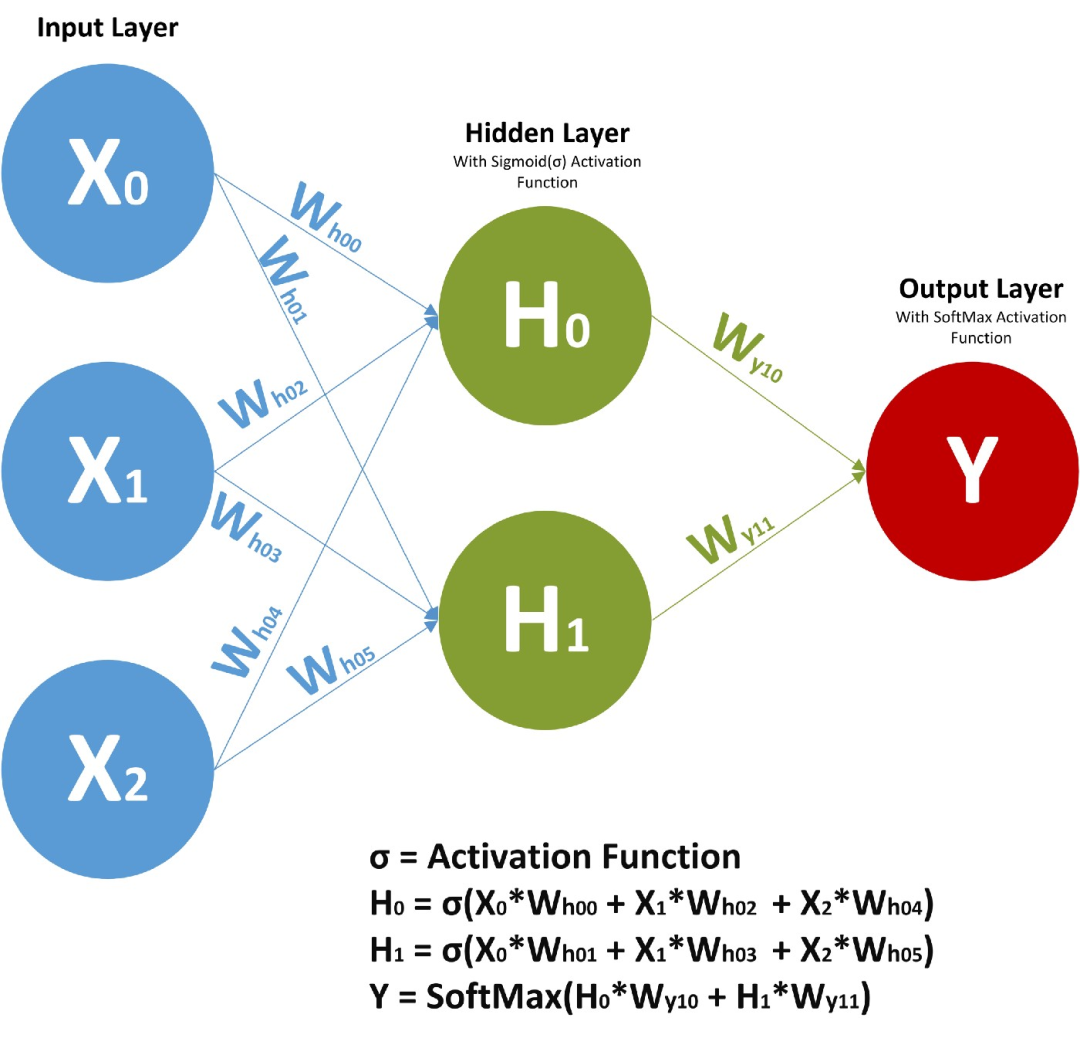
在前饋神經網絡中,我們有 X(輸入)、H(隱藏)和 Y(輸出)。我們可以有任意多的隱藏層,但是每個隱藏層的權值 W 和每個神經元對應的輸入權值是不同的。
上面,我們有權值 Wy10 和 Wy11,分別對應于兩個不同的層相對于輸出 Y 的權值,而 Wh00、Wh01 等代表了不同神經元相對于輸入的不同權值。
由于存在時間步長,神經網絡單元包含一組前饋神經網絡。該神經網絡具有順序輸入、順序輸出、多時間步長和多隱藏層的特點。
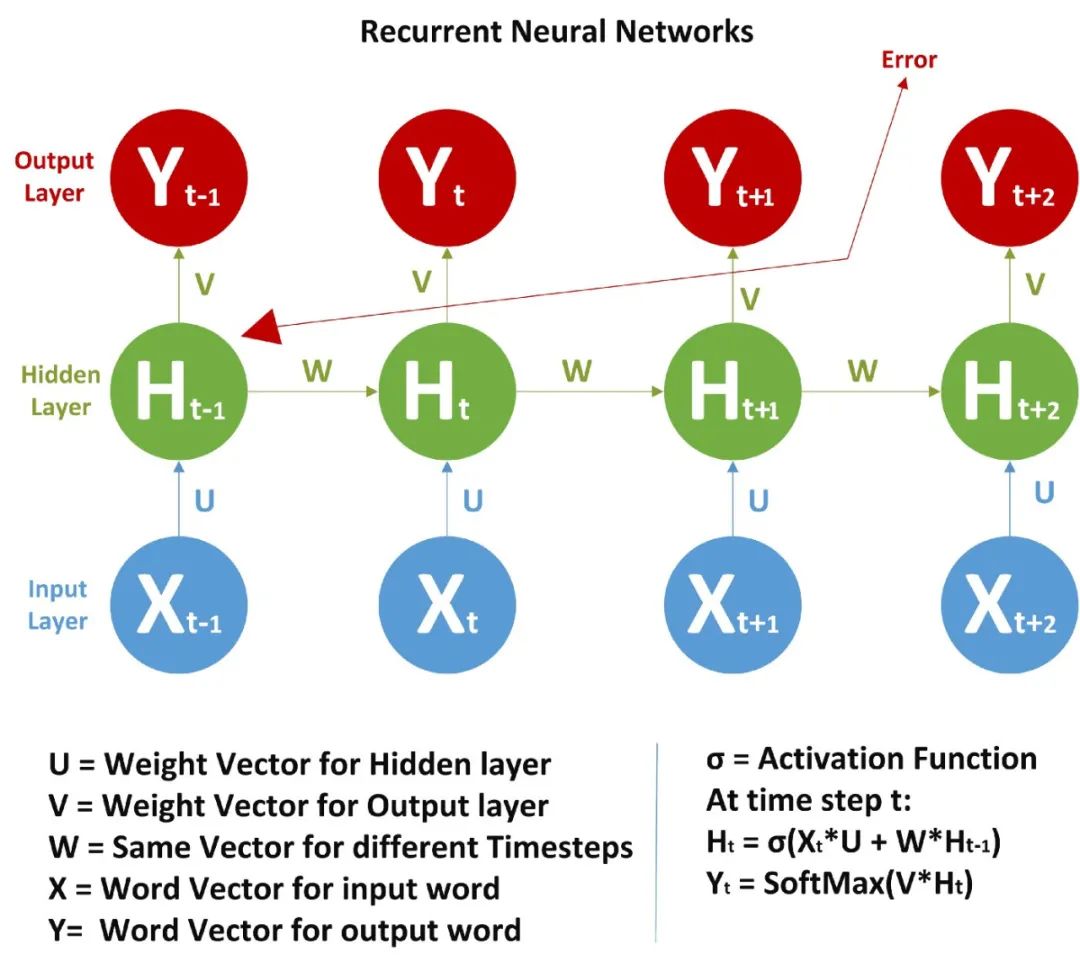
與 FFNN 不同的是,這里我們不僅從輸入值計算隱藏層值,還從之前的時間步長值計算隱藏層值。對于時間步長,隱藏層的權值(W)是相同的。下面展示的是 RNN 以及它涉及的數學公式的完整圖片。
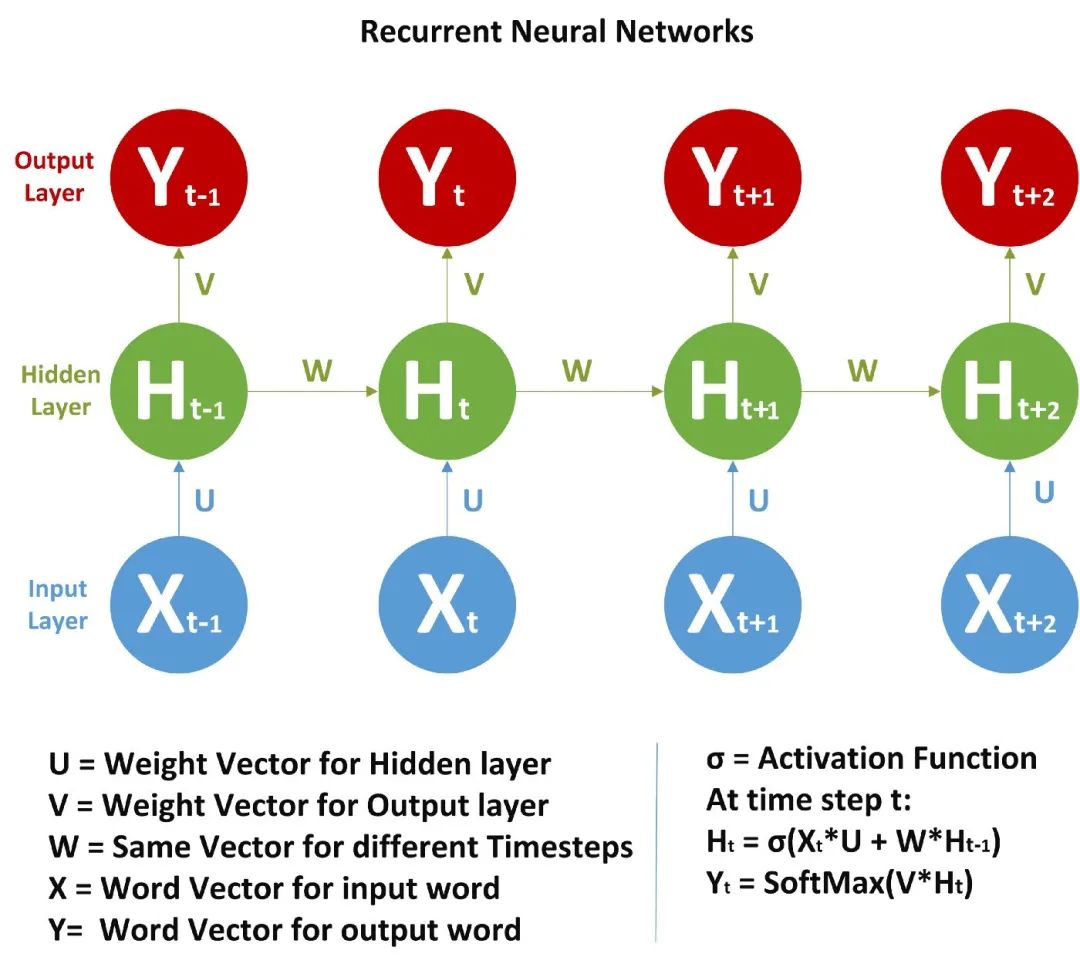
在圖片中,我們正在計算隱藏層的時間步長 t 的值:
上面我們只計算了 Ht,類似地,我們可以計算所有其他的時間步長。
步驟:
1、從
2、由
3、從
4、由
需要注意的是:
1、
2、我們甚至可以先計算隱藏層(所有時間步長),然后計算
3、權重向量一開始是隨機的。
一旦前饋輸入完成,我們就需要計算誤差并使用反向傳播法來反向傳播誤差,我們使用交叉熵作為代價函數。
如果你知道正常的神經網絡是如何工作的,剩下的就很簡單了,如果不清楚,可以參考本號前面關于人工神經網絡的文章。
我們需要計算下面各項,
因為 W 對于所有的時間步長都是一樣的,我們需要返回到前面,來進行更新。
記住 RNN 的反向傳播和人工神經網絡的反向傳播是一樣的,但是這里的當前時間步長是基于之前的時間步長計算的,所以我們必須從頭到尾遍歷來回。
如果我們運用鏈式法則,就像這樣

在所有時間步長上的 W 都相同,因此按鏈式法則展開項越來越多。
在 Richard Sochers 的循環神經網絡講座幻燈片[1]中,可以看到一種類似但不同的計算公式的方法。
所以這里,
現在我們回過頭來談談我們的情感分析問題,這里有一個 RNN,
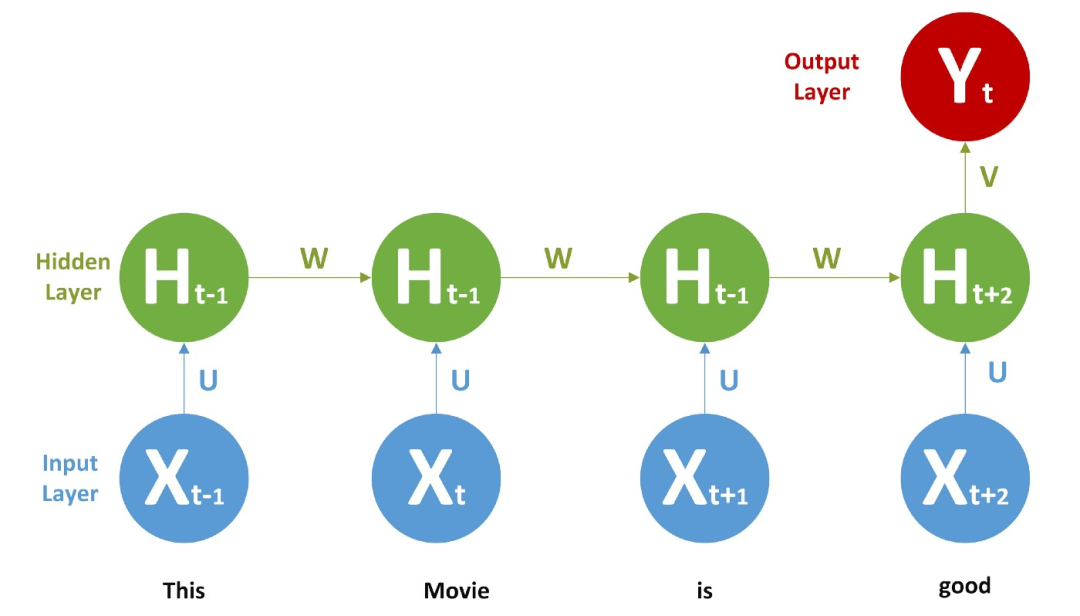
我們給每個單詞提供一個詞向量或者一個熱編碼向量作為輸入,并進行前饋和 BPTT,一旦訓練完成,我們就可以給出新的文本來進行預測。它會學到一些東西,比如不+積極的詞 = 消極的。
RNN 的問題 → 消失/爆炸梯度問題
由于 W 對于所有的時間步長都是一樣的,在反向傳播過程中,當我們回去調整權重時,信號會變得要么太弱要么太強,從而導致要么消失要么爆炸的問題。
關于RNN背后的數學原理是什么問題的解答就分享到這里了,希望以上內容可以對大家有一定的幫助,如果你還有很多疑惑沒有解開,可以關注億速云行業資訊頻道了解更多相關知識。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。