Contents

前言四種遍歷樹的方法簡介簡介兩種快速獲得遍歷結果的方法根據前序遍歷和后續遍歷創建樹代碼實現四種遍歷樹的方法的代碼

不說廢話了，下面講講如何根據pre_order和in_order創建二叉樹。

四種遍歷樹的方法簡介

簡介

首先這里簡單介紹一下二叉樹的4種遍歷方式：

• 前序遍歷（pre_order）

• 中序遍歷（in_order）

• 后序遍歷（post_order）

• 層序遍歷（level_order）

至于這些遍歷的代碼放在文章的最后。

前序遍歷就是先對當前的根節點進行操作，然后到左子節點，再到右子節點！

中序遍歷就是先對當前左子節點進行操作，然后到當前根節點，再到右子節點！

后序遍歷就是先對當前左子節點進行操作，然后到右子節點，再到當前根節點！

層序遍歷就是按照從上到下從左到右的順序對每個節點進行操作！代碼寫起來比前三個復雜點，得借助隊列，并用迭代的方式來做。

如下圖(之前上課做的筆記)：

兩種快速獲得遍歷結果的方法

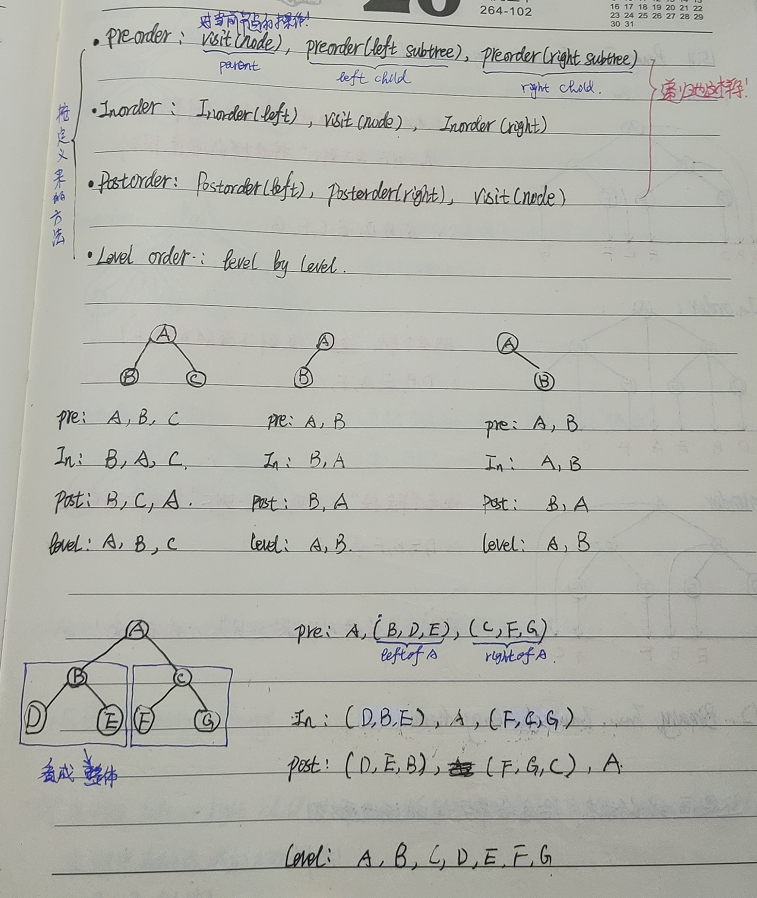
另外，介紹兩個 可以快速地 根據樹的形狀 得出 前序、后序、中序 的遍歷結果。

法一：

法二：

根據前序遍歷和后續遍歷創建樹

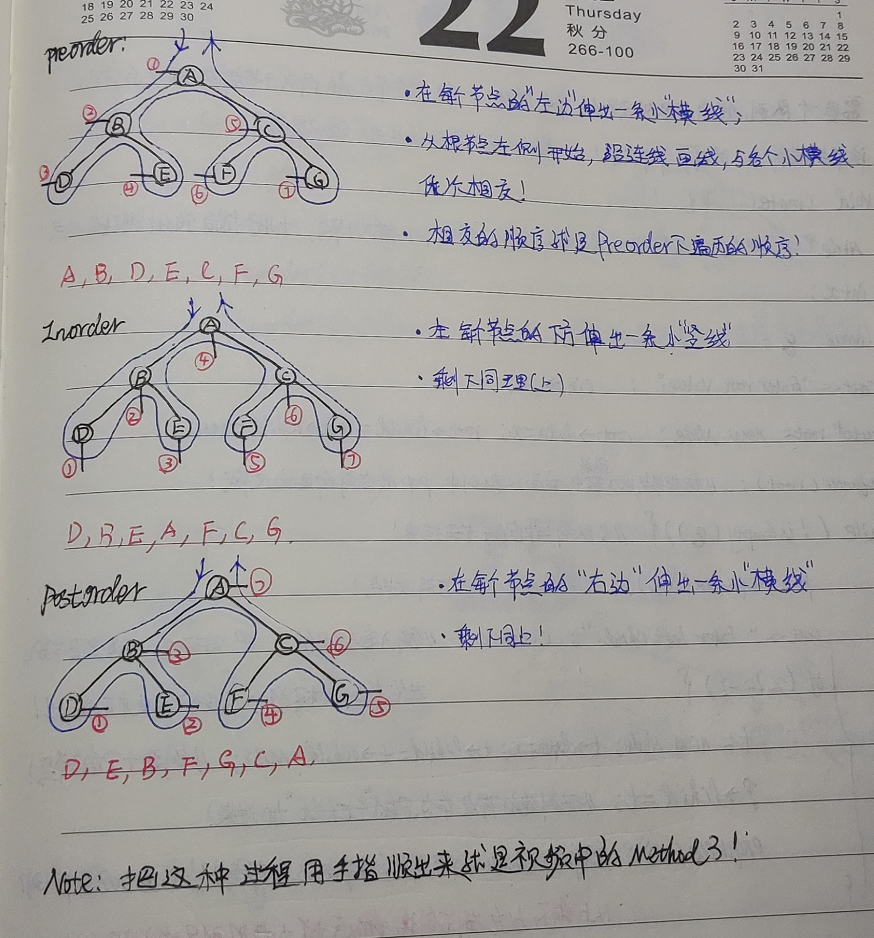
給你一個數組，用這個數組的值來創建一個樹，結果有多種可能：

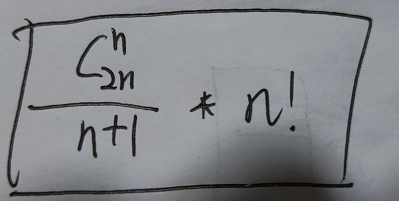
其中n是數組中元素的個數！

但是，如果我們給了兩個數組，分別是前序遍歷和后續遍歷的結果，那么我們就能創建唯一的一個樹！

Note：要求數組中的元素不重復，是唯一的！

看過上面對樹的那幾種遍歷方式后，可以發現：

Note：下面的這個過程有點枯燥，我表述地也不太好，可以看后面的圖。

• 前序遍歷的第一個元素就是樹的根節點；第二個元素是根節點的左子節點，這個左子節點也是后面的根節點；

• 根節點把中序遍歷的數組一分為二，中序遍歷的數組中：根節點的左邊是左樹，根節點的右邊是右樹

• 

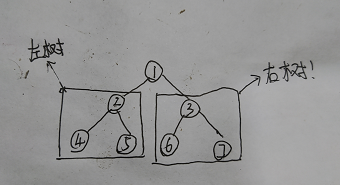
• 所以，我們就對前序遍歷的數組進行遍歷，當前索引記為pre_i，在每次遍歷中，到中序遍歷的數組中找這個pre_i對應的值，用這個pre_i把中序遍歷的結果一分為二。這樣往復下去就能還原樹了。

下面我畫一下整個流程：

大概就是這樣，不斷地對中序遍歷的數組一分為二（根據前序遍歷的數組的當前元素進行分割）；中序遍歷的數組的當前元素就是當前的根節點。

代碼實現

先定義樹的節點：

template <class T>
struct Node{
    T val;
    Node* left;
    Node* right;

    explicit Node(T v) : val(v), left(nullptr), right(nullptr){}
};

根據前序遍歷和中序遍歷創建樹：

/**
 * @brief 根據前序遍歷和中序遍歷創建樹
 * @param[in] pre_vec   前序遍歷的數組
 * @param[in] in_vec    中序遍歷的數組
 * @param[in] left_in   中序遍歷當前段的左邊界
 * @param[in] right_in  中序遍歷當前段的右邊界（超尾）
 * @static pre_i        前序遍歷的當前的索引
 *
 * @note 在每一層遞歸中，當前的 中序遍歷 數組段 被分為：[left_in, pre_i), pre_i, [pre_i+1, right_in)
 * */
template <class T>
Node<T>* CreateTreeR(vector<T>& pre_vec, vector<T>& in_vec, int left_in, int right_in)
{
    static int pre_i = 0;

    if (left_in < right_in)
    {
        /// 從 前序遍歷 的數組中 獲取 當前 根節點！
        T cur_root_val = pre_vec.at(pre_i);
        auto* cur_root = new Node<T>(cur_root_val);

        /// 遍歷 中序遍歷 的數組，找到當前根節點對應的索引
        int i = left_in;
        while (i < right_in && cur_root_val != in_vec.at(i)) ++i;

        /// 下次遞歸前 pre_i 是需要向后移動一位的
        ++pre_i;

        /// 一分為二！(注意，i是當前節點的索引哦！)
        cur_root->left  = CreateTreeR(pre_vec, in_vec, left_in, i);              /// 左樹
        cur_root->right = CreateTreeR(pre_vec, in_vec, i+1, right_in);   /// 右樹

        return cur_root;
    }

    /// 當分到只剩最后一個元素時就返回空了
    return nullptr;
}

測試這段程序

對創建出來的這個樹，用四種遍歷方法分別遍歷一下子，四種遍歷的代碼在文末。

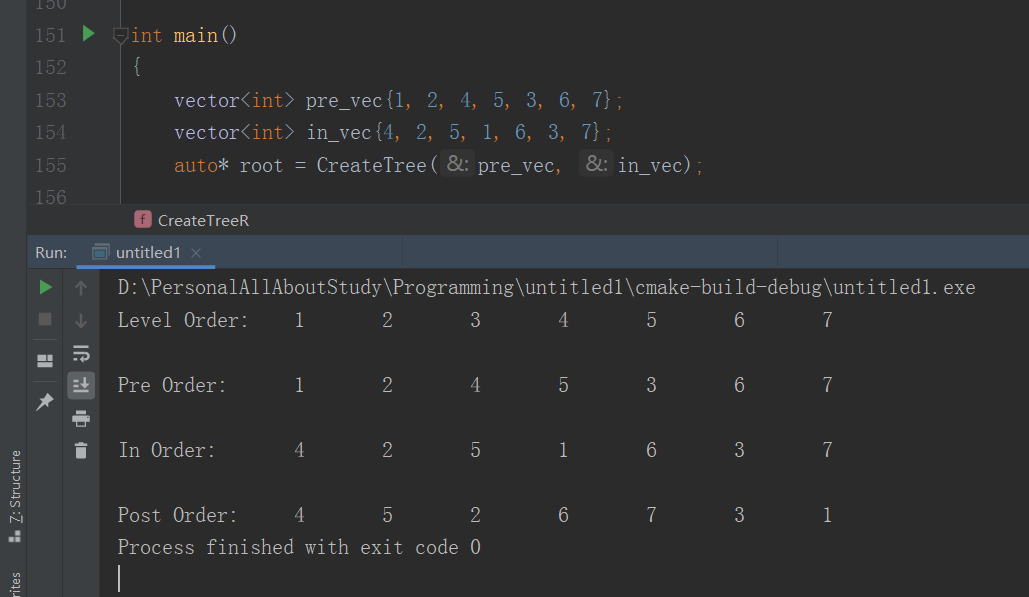
上面這個是數字的，我現在拿字符串的試試：

四種遍歷樹的方法的代碼

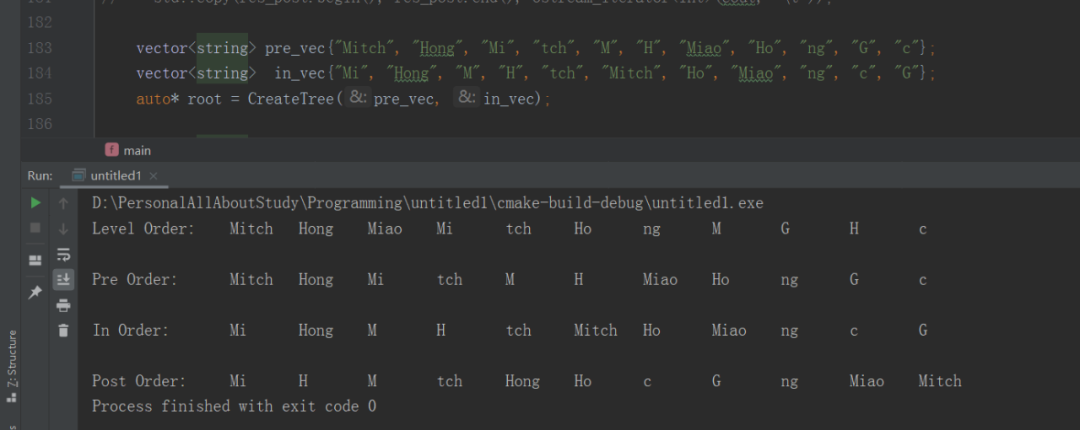
1.層序遍歷：

/**
 * @brief 樹的層序遍歷
 * */
 template<class T>
 void LevelOrder(Node<T>* root, vector<T>& vec)
{
     /// 如果根節點為空就直接返回
     if (!root) return;

     /// 定義一個隊列放所有可能會成為 "根節點" 的節點（每次循環中都會pop出一個 "根節點" ）
     queue< Node<T>* > q;
     q.push(root);

     while (!q.empty())
     {
         /// 從隊列中拿出最前面的根節點
         Node<T>* cur_root = q.front();  /// 這個變量在while外面聲明更好，不用每次都創建一個新變量。
         q.pop();
         /// 保存當前 "根節點" 的值
         vec.push_back(cur_root->val);

         /// 如果左子節點非空就把左子節點放入隊列
         if (cur_root->left)
             q.push(cur_root->left);

         /// 如果右子節點非空就把右子節點放入隊列
         if (cur_root->right)
             q.push(cur_root->right);
     }
}

2.前序遍歷：

/**
 * @brief 樹的前序遍歷
 * */
template<class T>
void PreOrder(Node<T>* root, vector<T>& vec)
{
    if (root)
    {
        vec.push_back(root->val);
        PreOrder(root->left, vec);
        PreOrder(root->right, vec);
    }
}

3.中序遍歷：

/**
 * @brief 樹的中序遍歷
 * */
template<class T>
void InOrder(Node<T>* root, vector<T>& vec)
{
    if (root)
    {
        InOrder(root->left, vec);
        vec.push_back(root->val);
        InOrder(root->right, vec);
    }
}

4.后序遍歷：

/**
 * @brief 樹的后序遍歷
 * */
template<class T>
void PostOrder(Node<T>* root, vector<T>& vec)
{
    if (root)
    {
        PostOrder(root->left, vec);
        PostOrder(root->right, vec);
        vec.push_back(root->val);
    }
}