您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇文章給大家分享的是有關K 均值算法是如何讓數據自動分組,小編覺得挺實用的,因此分享給大家學習,希望大家閱讀完這篇文章后可以有所收獲,話不多說,跟著小編一起來看看吧。
下面要介紹的K 均值算法是一種無監督學習。
與分類算法相比,無監督學習算法又叫聚類算法,就是只有特征數據,沒有目標數據,讓算法自動從數據中“學習知識”,將不同類別的數據聚集到相應的類別中。
K 均值的英文為K-Means,其含義是:
K:表示該算法可以將數據劃分到K 個不同的組中。
均值:表示每個組的中心點是組內所有值的平均值。
K 均值算法可以將一個沒有被分類的數據集,劃分到K 個類中。某個數據應該被劃分到哪個類,是通過該數據與群組中心點的相似度決定的,也就是該數據與哪個類的中心點最相似,則該數據就應該被劃分到哪個類中。
關于如何計算事物之間的相似度,可以參考文章《計算機如何理解事物的相關性》。
使用K 均值算法的一般步驟是:
確定K 值是多少:
對于K 值的選擇,可以通過分析數據,估算數據應該分為幾個類。
如果無法估計確切值,可以多試幾個K 值,最終將劃分效果最好的K 值作為最終選擇。
選擇K 個中心點:一般最開始的K 個中心點是隨機選擇的。
將數據集中的所有數據,通過與中心點的相似度劃分到不同的類別中。
根據類別中的數據平均值,重新計算每個類別中心點的位置。
循環迭代第3,4步,直到中心點的位置幾乎不再改變,分類過程就算完畢。
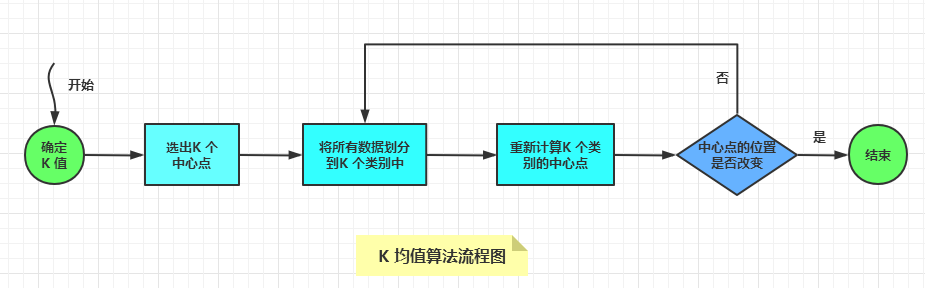
下面以一個二維數據點的聚類過程,來看下K 均值算法如何聚類。
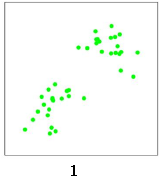
首先,這里有一些離散的數據點,如下圖:
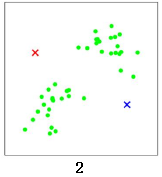
我們使用K 均值算法對這些數據點進行聚類。隨機選擇兩個點作為兩個類的中心點,分別是紅色x 和藍色x:
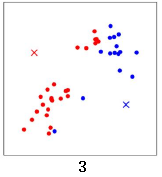
計算所有數據點到這兩個中心點的距離,距離紅色x 近的點標紅色,距離藍色x 近的點標藍色:
重新計算兩個中心點的位置,兩個中心點分別移動到新的位置:
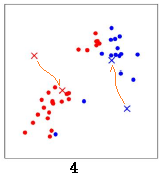
重新計算所有數據點分別到紅色x 和藍色x的距離,距離紅色x 近的點標紅色,距離藍色x 近的點標藍色:
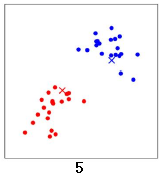
再次計算兩個中心點的位置,兩個中心點分別移動到新的位置:
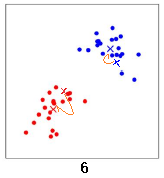
直到中心點的位置幾乎不再變化,聚類結束。
以上過程就是K 均值算法的聚類過程。
K 均值算法是一個聚類算法,sklearn 庫中的 cluster 模塊實現了一系列的聚類算法,其中就包括K 均值算法。
來看下KMeans 類的原型:
KMeans( n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='deprecated', verbose=0, random_state=None, copy_x=True, n_jobs='deprecated', algorithm='auto')
可以看KMeans 類有很多參數,這里介紹幾個比較重要的參數:
n_clusters: 即 K 值,可以隨機設置一些 K 值,選擇聚類效果最好的作為最終的 K 值。
init:選擇初始中心點的方式:
init='k-means++':可加快收斂速度,是默認方式,也是比較好的方式。
init='random ':隨機選擇中心點。
也可以自定義方式,這里不多介紹。
n_init:初始化中心點的運算次數,默認是 10。如果 K 值比較大,可以適當增大 n_init 的值。
algorithm:k-means 的實現算法,有auto,full,elkan三種。
默認是auto,根據數據的特點自動選擇用full或者elkan。
max_iter:算法的最大迭代次數,默認是300。
如果聚類很難收斂,設置最大迭代次數可以讓算法盡快結束。
下面對一些二維坐標中的點進行聚類,看下如何使用K 均值算法。
下面是隨機生成的三類坐標點,每類有20 個點,不同類的點的坐標在不同的范圍內:
A 類點:Ax 表示A 類點的橫坐標,Ay 表示A 類點的縱坐標。橫縱坐標范圍都是 (0, 20]。
B 類點:Bx 表示B 類點的橫坐標,By 表示B 類點的縱坐標。橫縱坐標范圍都是 (40, 60]。
C 類點:Cx 表示C 類點的橫坐標,Cy 表示C 類點的縱坐標。橫縱坐標范圍都是 (70, 90]。
Ax = [20, 6, 14, 13, 8, 19, 20, 14, 2, 11, 2, 15, 19, 4, 4, 11, 13, 4, 15, 11] Ay = [14, 19, 17, 16, 3, 7, 9, 18, 20, 3, 4, 12, 9, 17, 14, 1, 18, 17, 3, 5] Bx = [53, 50, 46, 52, 57, 42, 47, 55, 56, 57, 56, 50, 46, 46, 44, 44, 58, 54, 47, 57] By = [60, 57, 57, 53, 54, 45, 54, 57, 49, 53, 42, 59, 54, 53, 50, 50, 58, 58, 58, 51] Cx = [77, 75, 71, 87, 74, 70, 74, 85, 71, 75, 72, 82, 81, 70, 72, 71, 88, 71, 72, 80] Cy = [85, 77, 82, 87, 71, 71, 77, 88, 81, 73, 80, 72, 90, 77, 89, 88, 83, 77, 90, 72]
我們可以用 Matplotlib 將這些點畫在二維坐標中,代碼如下:
import matplotlib.pyplot as plt plt.scatter(Ax + Bx + Cx, Ay + By + Cy, marker='o') plt.show()
畫出來的圖如下,可看到這三類點的分布范圍還是一目了然的。
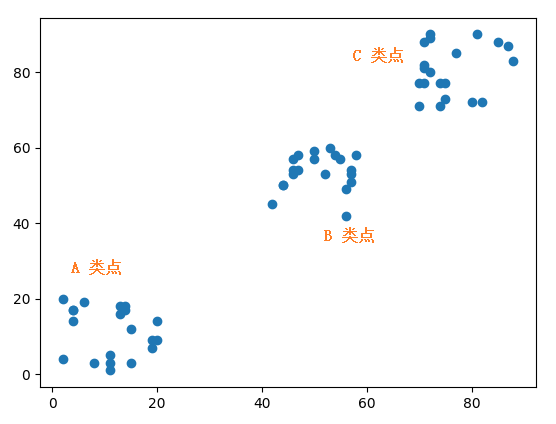
關于如何使用 Matplotlib 繪圖,可以參考文章《如何使用Python 進行數據可視化》。
下面使用K 均值算法對數據點進行聚類。
創建K 均值模型對象:
from sklearn.cluster import KMeans # 設置 K 值為 3,其它參數使用默認值 kmeans = KMeans(n_clusters=3)
準備數據,共三大類,60 個坐標點:
train_data = [ # 前20 個為 A 類點 [20, 14], [6, 19], [14, 17], [13, 16], [8, 3], [19, 7], [20, 9], [14, 18], [2, 20], [11, 3], [2, 4], [15, 12], [19, 9], [4, 17], [4, 14], [11, 1], [13, 18], [4, 17], [15, 3], [11, 5], # 中間20 個為B 類點 [53, 60], [50, 57], [46, 57], [52, 53], [57, 54], [42, 45], [47, 54], [55, 57], [56, 49], [57, 53], [56, 42], [50, 59], [46, 54], [46, 53], [44, 50], [44, 50], [58, 58], [54, 58], [47, 58], [57, 51], # 最后20 個為C 類點 [77, 85], [75, 77], [71, 82], [87, 87], [74, 71], [70, 71], [74, 77], [85, 88], [71, 81], [75, 73], [72, 80], [82, 72], [81, 90], [70, 77], [72, 89], [71, 88], [88, 83], [71, 77], [72, 90], [80, 72], ]
擬合模型:
kmeans.fit(train_data)
對數據進行聚類:
predict_data = kmeans.predict(train_data)
查看聚類結果,其中的0,1,2 分別代表不同的類別:
>>> print(predict_data) [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
通過觀察最終的聚類結果predict_data,可以看到,前,中,后20 個數據分別被分到了不同的類中,也非常符合我們的預期,說明K 均值算法的聚類結果還是很不錯的 。
因為本例中的二維坐標點的分布界限非常明顯,所以最終的聚類結果非常不錯。
我們可以通過 n_iter_ 屬性來查看迭代的次數:
>>> kmeans.n_iter_ 2
通過 cluster_centers_ 屬性查看每個類的中心點坐標:
>>> kmeans.cluster_centers_ array([[11.25, 11.3 ], [75.9 , 80.5 ], [50.85, 53.6 ]])
將這三個中心點畫在坐標軸中,如下:
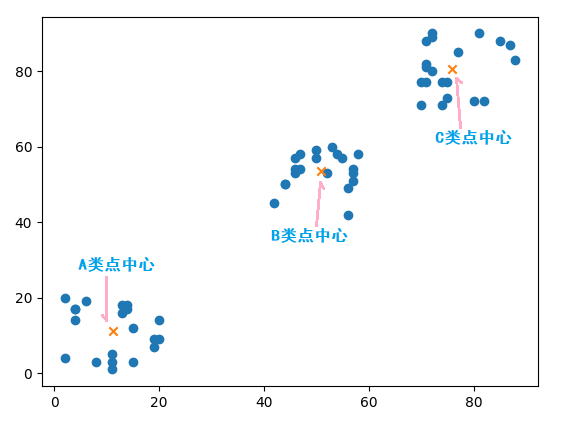
以上就是K 均值算法是如何讓數據自動分組,小編相信有部分知識點可能是我們日常工作會見到或用到的。希望你能通過這篇文章學到更多知識。更多詳情敬請關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。