有哪些圖形算法

本篇內容介紹了“有哪些圖形算法”的有關知識，在實際案例的操作過程中，不少人都會遇到這樣的困境，接下來就讓小編帶領大家學習一下如何處理這些情況吧！希望大家仔細閱讀，能夠學有所成！

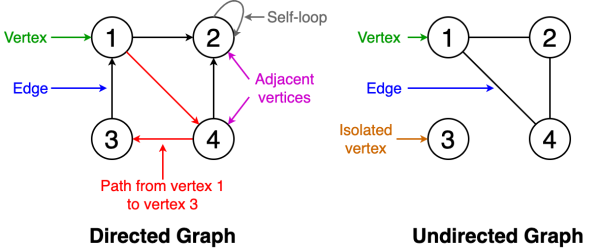
什么是圖?

一個圖由一組有限的頂點或節點以及一組連接這些頂點的邊組成。 如果兩個頂點通過同一邊彼此連接，則它們稱為相鄰頂點。

下面給出一些與圖有關的基本定義。 您可以參考圖1的示例。

• 順序：圖形中的頂點數

• 大小：圖形中的邊數

• 頂點度：入射到頂點的邊數

• 孤立的頂點：未連接到圖中任何其他頂點的頂點

• 自環：從頂點到自身的邊

• 有向圖：所有邊都有一個方向的圖，該方向指示什么是起始頂點，什么是終止頂點

• 無向圖：具有沒有方向的邊的圖

• 加權圖：圖的邊緣具有權重

• 未加權圖形：圖形的邊緣沒有權重

1.廣度優先搜索

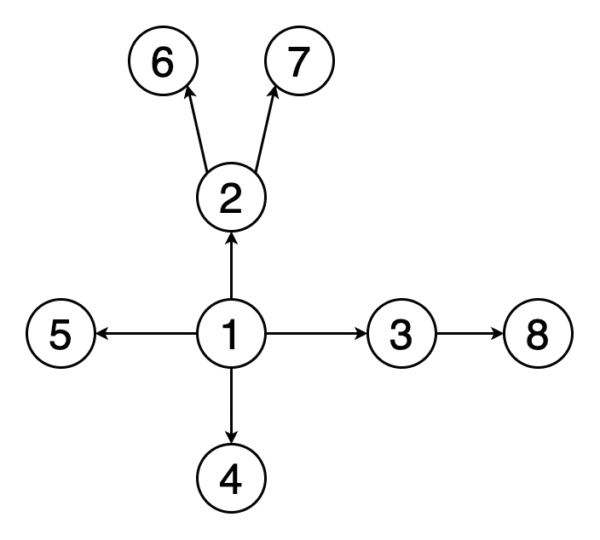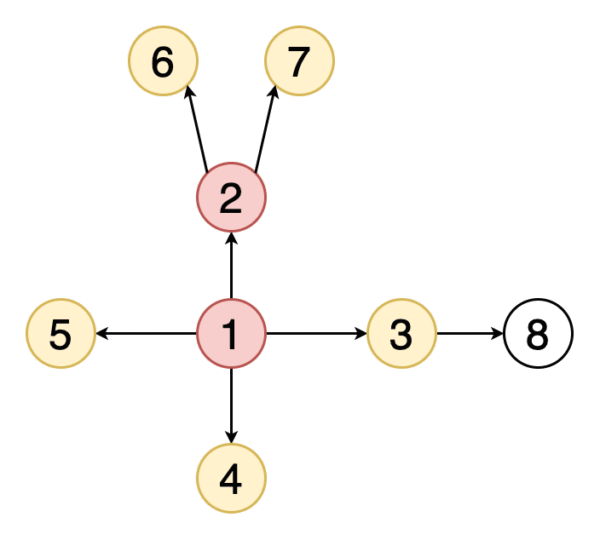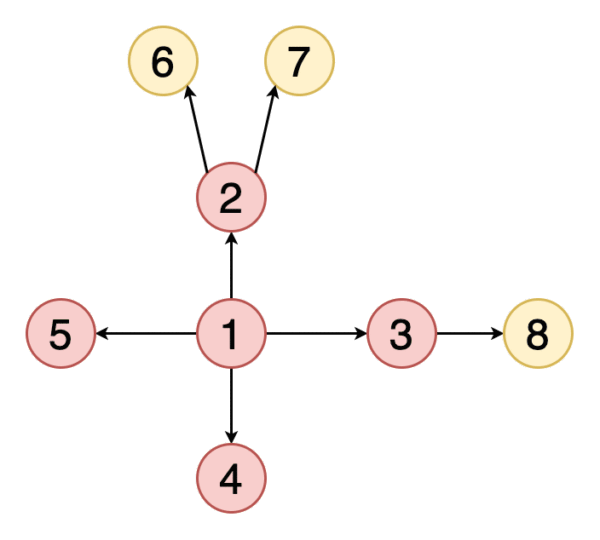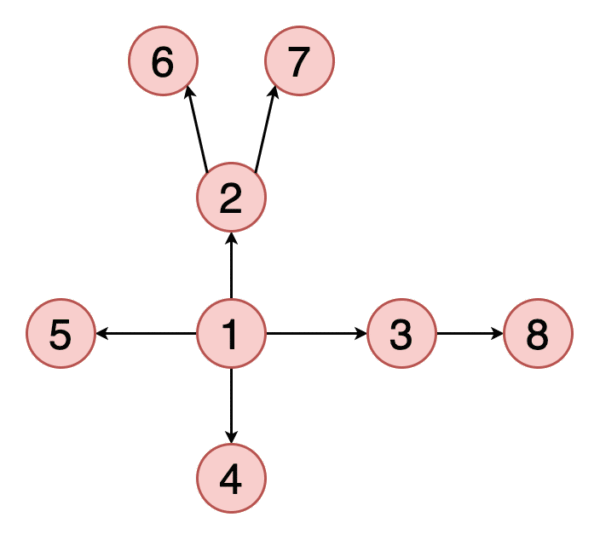
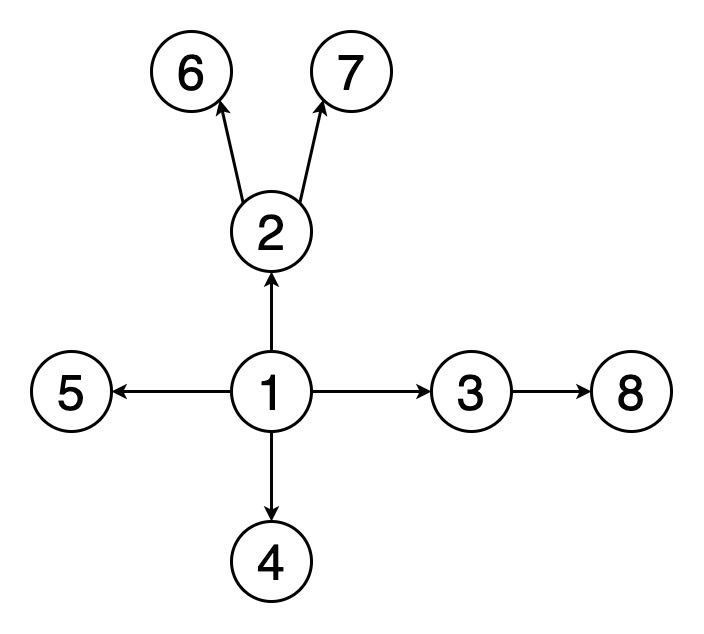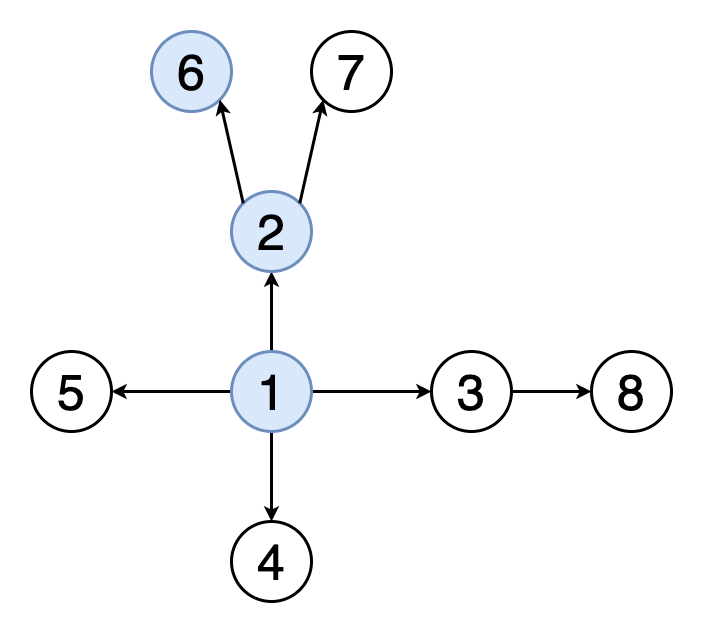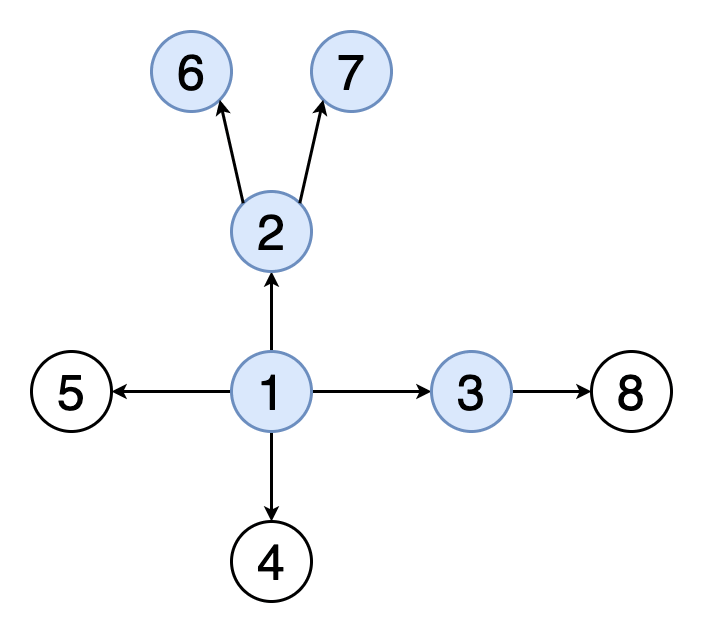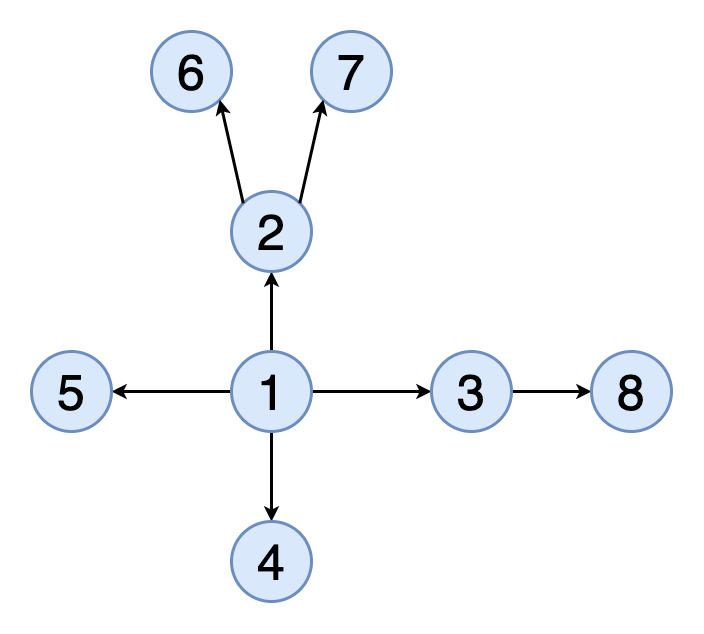
遍歷或搜索是可以在圖形上執行的基本操作之一。 在廣度優先搜索(BFS)中，我們從一個特定的頂點開始，并在當前深度探索其所有鄰居，然后再進入下一級的頂點。  與樹不同，圖可以包含循環(第一個頂點和最后一個頂點相同的路徑)。 因此，我們必須跟蹤訪問的頂點。 在實現BFS時，我們使用隊列數據結構。

圖2表示示例圖的BFS遍歷的動畫。 注意如何發現頂點(黃色)并訪問頂點(紅色)。

應用領域

• 用于確定最短路徑和最小生成樹。

• 搜索引擎搜尋器用來構建網頁索引。

• 用于在社交網絡上搜索。

• 用于查找對等網絡(例如BitTorrent)中的可用鄰居節點。

2.深度優先搜索

在深度優先搜索(DFS)中，我們從特定的頂點開始，并在回溯(回溯)之前沿每個分支進行盡可能的探索。 在DFS中，我們還必須跟蹤訪問的頂點。  在實現DFS時，我們使用堆棧數據結構來支持回溯。

圖3表示與圖2相同的示例圖的DFS遍歷的動畫。請注意，它如何遍歷深度和回溯。

應用領域

• 用于查找兩個頂點之間的路徑。

• 用于檢測圖中的周期。

• 用于拓撲排序。

• 用于解決只有一種解決方案(例如迷宮)的難題

3.最短路徑

從一個頂點到另一個頂點的最短路徑是圖形中的一條路徑，因此應移動的邊的權重之和最小。

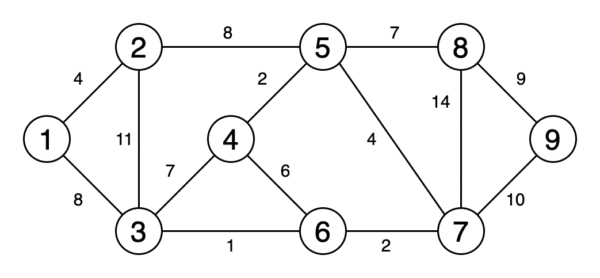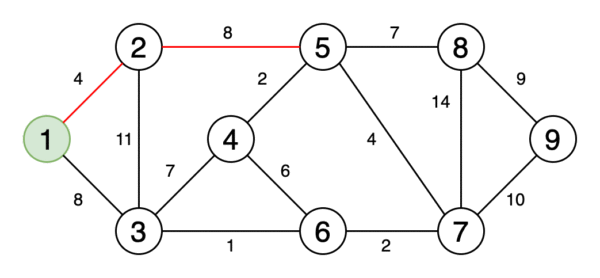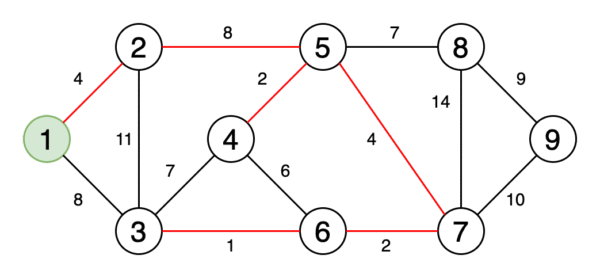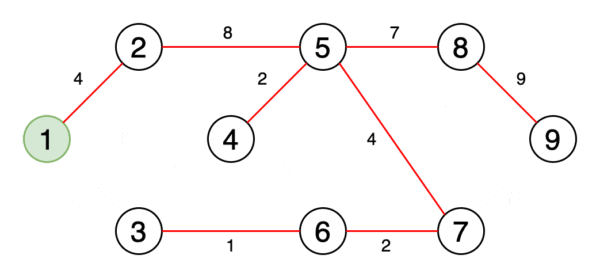
圖4顯示了一個動畫，其中確定了圖形中從頂點1到頂點6的最短路徑。

演算法

• Dijkstra最短路徑算法

• Bellman–Ford算法

應用領域

• 用于在Google地圖或Apple地圖等地圖軟件中查找從一個位置到另一個位置的路線。

• 用于網絡中以解決最小延遲路徑問題。

• 用于抽象機器中，以通過在不同狀態之間進行轉換來確定達到某個目標狀態的選擇(例如，可用于確定贏得一場比賽的最小可能次數)。

4.循環檢測

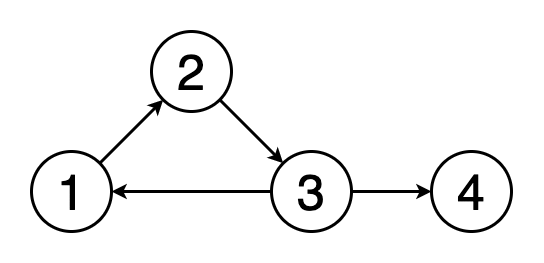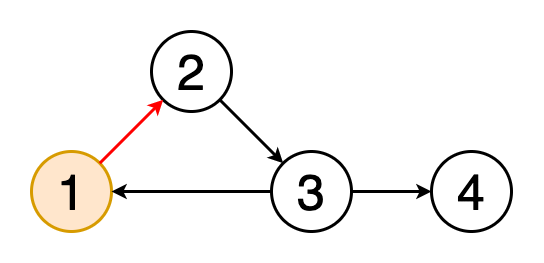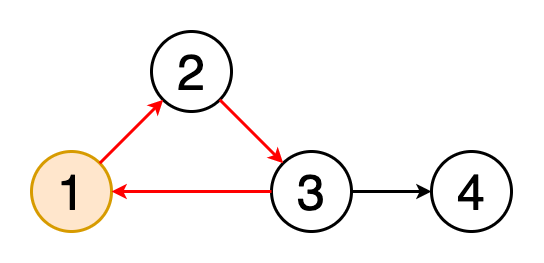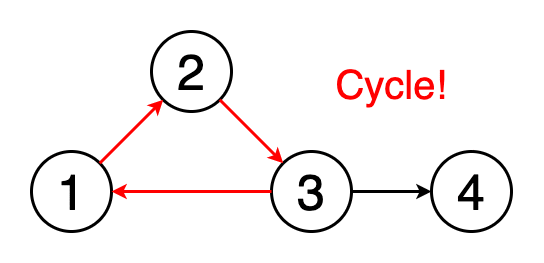
循環是圖形中的第一個頂點和最后一個頂點相同的路徑。 如果我們從一個頂點開始，沿著一條路徑行進，然后在起始頂點處結束，那么這條路徑就是一個循環。  循環檢測是檢測這些循環的過程。 圖5顯示了遍歷一個循環的動畫。

演算法

• 弗洛伊德循環檢測算法

• 布倫特算法

應用領域

• 用于基于分布式消息的算法。

• 用于在群集上使用分布式處理系統處理大規模圖形。

• 用于檢測并發系統中的死鎖。

• 在加密應用程序中用于確定消息的密鑰，該密鑰可以將該消息映射到相同的加密值。

5.最小生成樹

最小生成樹是圖的邊緣的子集，該圖以最小的邊權重之和連接所有頂點，并且不包含循環。

圖6是一個動畫，顯示了獲取最小生成樹的過程。

演算法

• Prim的算法

• Kruskal的算法

應用領域

• 用于構造樹以在計算機網絡中廣播。

• 用于基于圖的聚類分析。

• 用于圖像分割。

• 用于將社會區域劃分為連續區域的社會地理區域的區域化。

6.牢固連接的組件

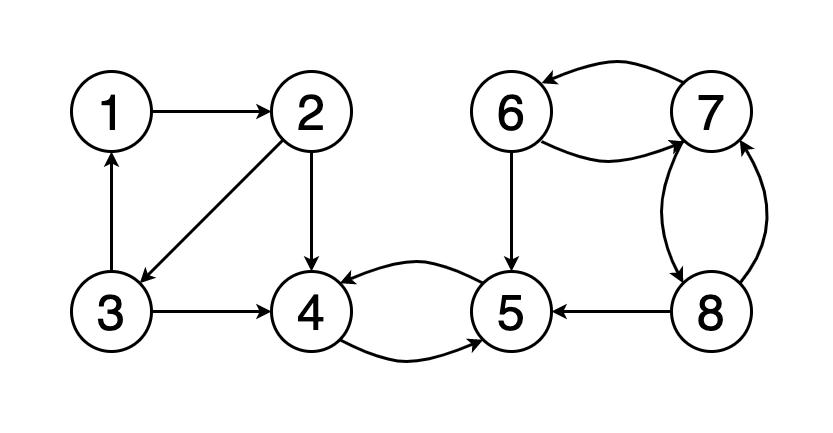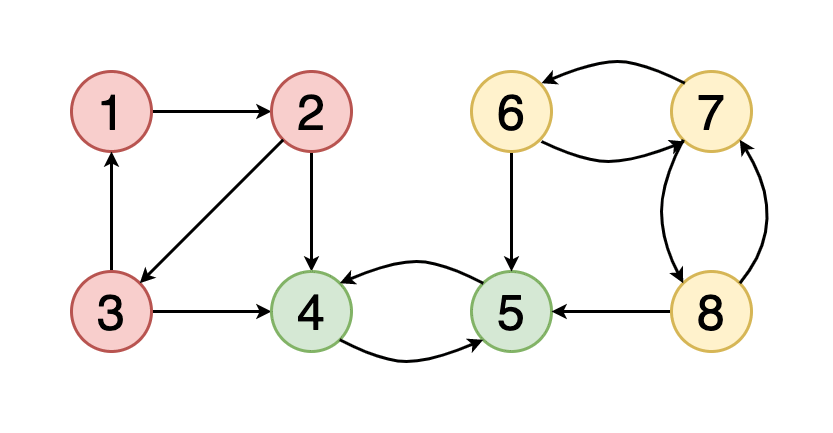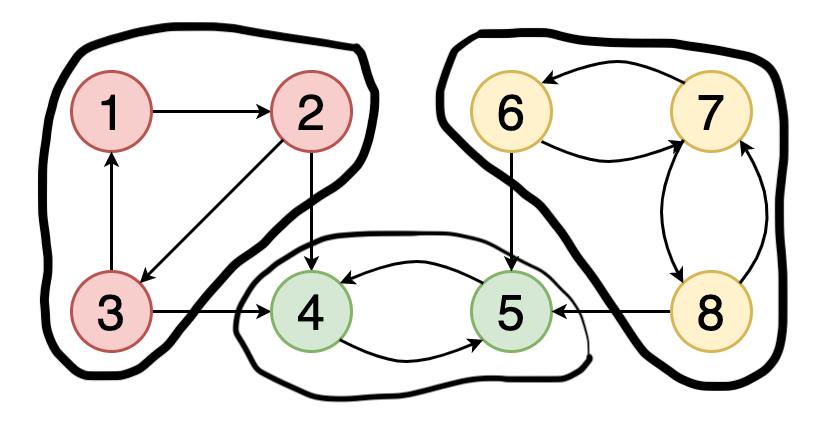
如果圖中的每個頂點均可從其他每個頂點到達，則稱該圖是牢固連接的。

圖7顯示了一個示例圖，其中包含三個具有紅色，綠色和黃色的頂點的牢固連接的組件。

演算法

• Kosaraju的算法

• Tarjan的強連接組件算法

應用領域

• 用于計算Dulmage–Mendelsohn分解，這是二部圖邊緣的分類。

• 用于社交網絡中，以找到一群緊密聯系并根據共同興趣提出建議的人。

7.拓撲排序

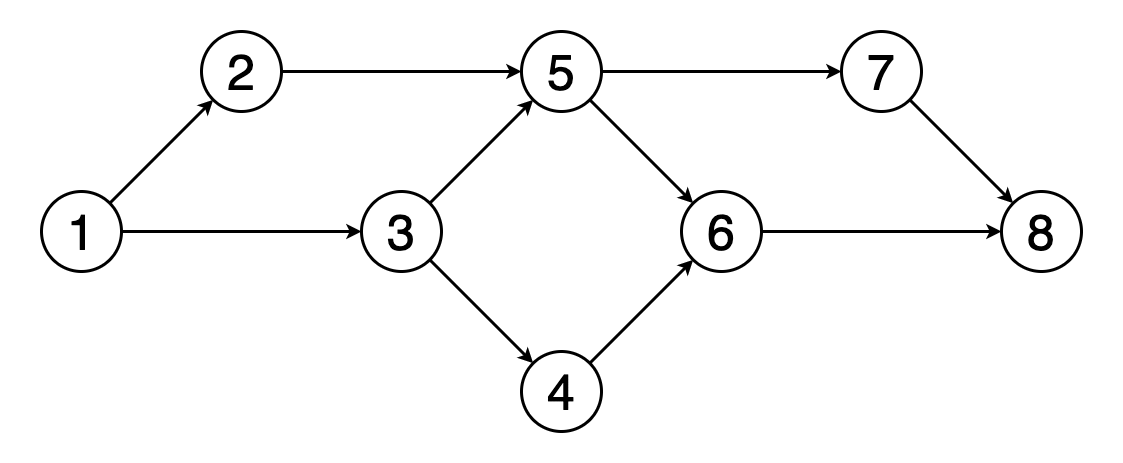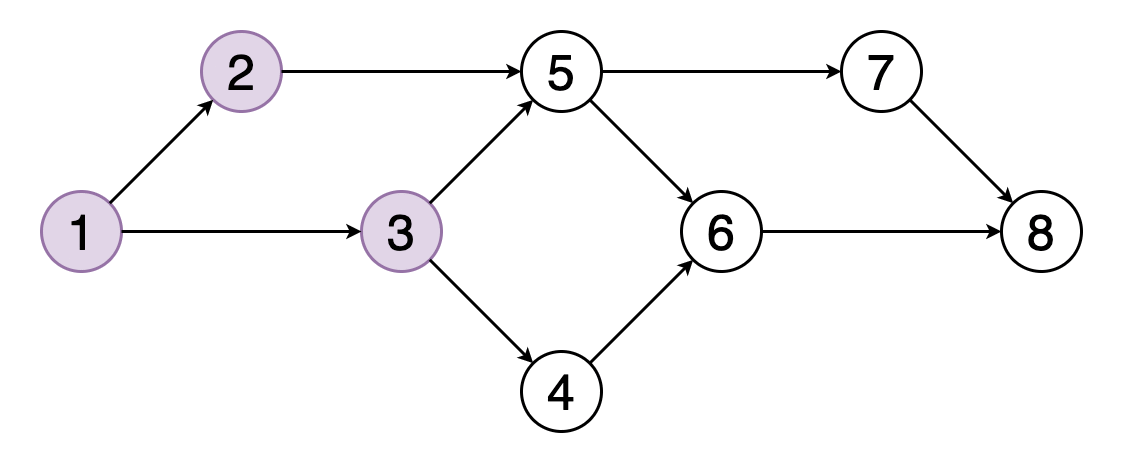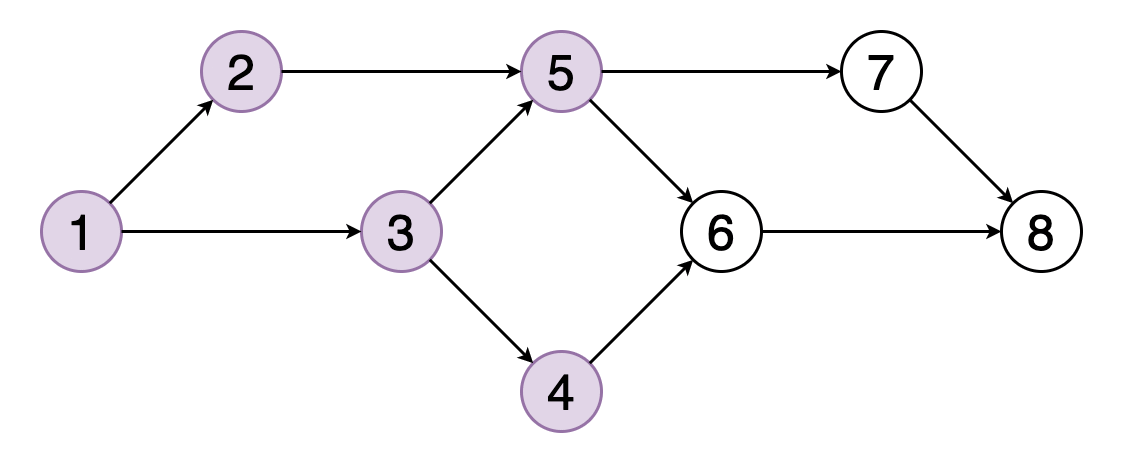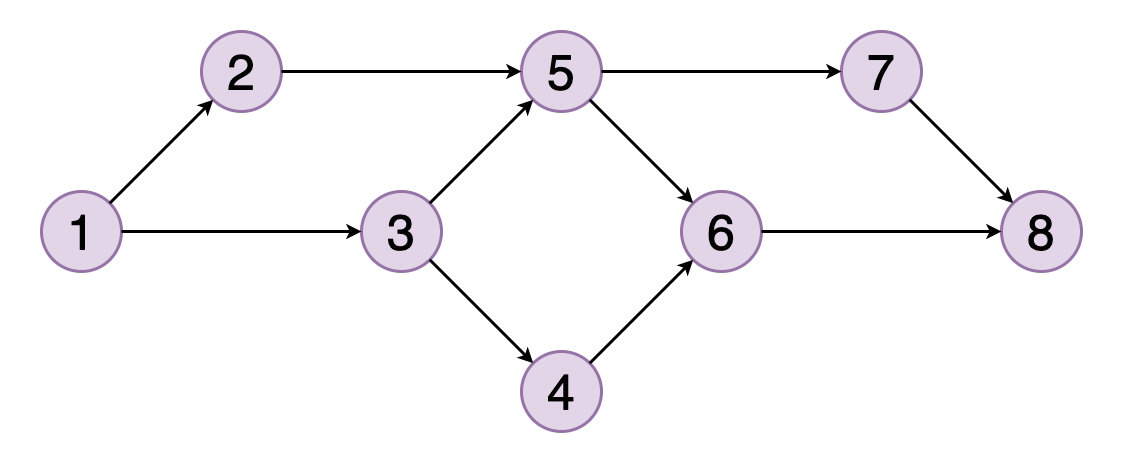
圖的拓撲排序是其頂點的線性排序，因此對于排序中的每個有向邊(u，v)，頂點u都位于v之前。

圖8顯示了頂點(1、2、3、5、4、6、7、8)的拓撲順序的示例。 您可以看到頂點5應該位于頂點2和3之后。類似地，頂點6應該位于頂點4和5之后。

演算法

• 卡恩算法

• 基于深度優先搜索的算法

應用領域

• 用于指令調度。

• 用于數據序列化。

• 用于確定在makefile中執行的編譯任務的順序。

• 用于解析鏈接器中的符號依賴性。

8.圖形著色

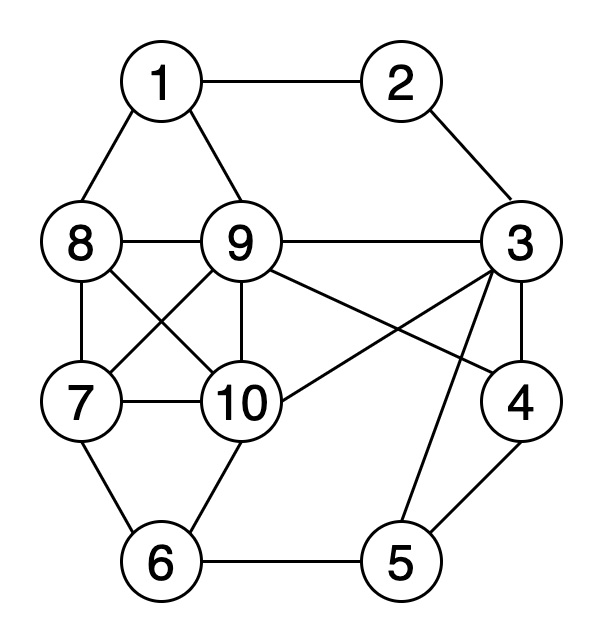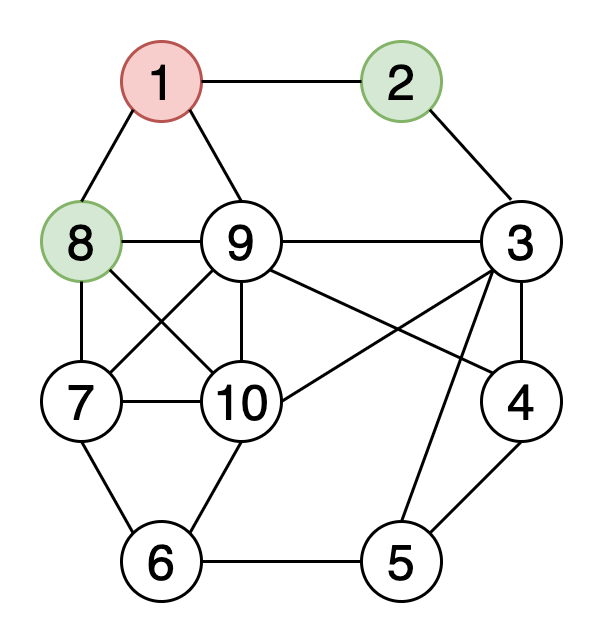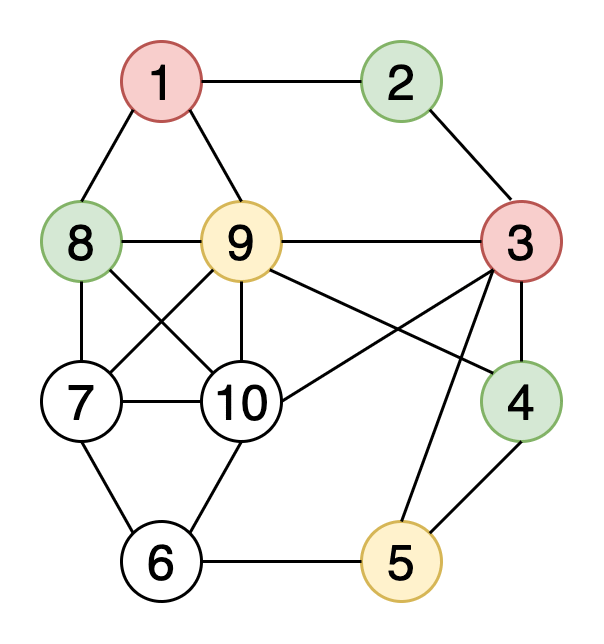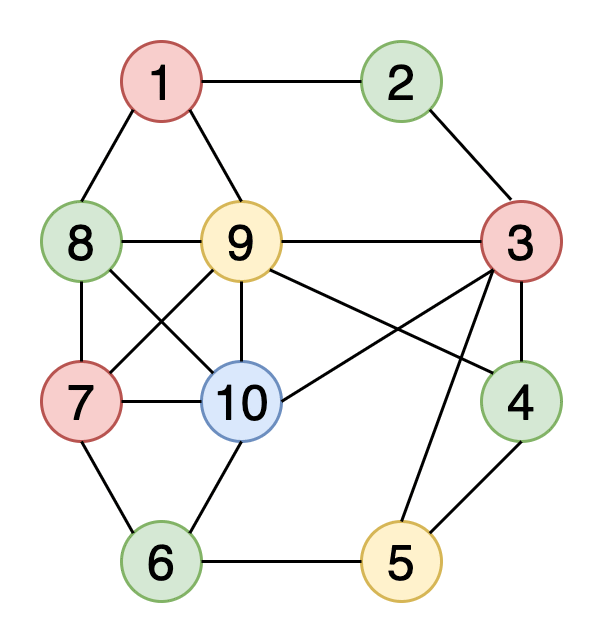
圖形著色可在確保某些條件的同時為圖形元素分配顏色。 頂點著色是最常用的圖形著色技術。  在頂點著色中，我們嘗試使用k種顏色為圖形的頂點著色，并且任何兩個相鄰的頂點都不應具有相同的顏色。 其他著色技術包括邊緣著色和面部著色。

圖的色數是為圖著色所需的最少顏色數。

圖9顯示了使用4種顏色的示例圖的頂點著色。

演算法

• 使用廣度優先搜索或深度優先搜索的算法

• 貪婪的著色

應用領域

• 用于安排時間表。

• 用于分配移動無線電頻率。

• 用于建模和求解數獨游戲。

• 用于檢查圖是否為二部圖。

• 用于為相鄰國家或地區具有不同顏色的國家或州的地理地圖著色。

9.最大流量

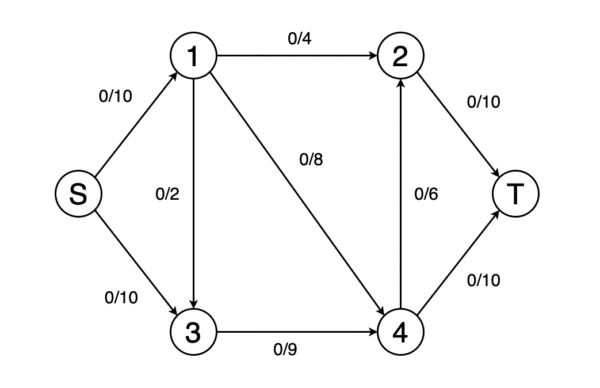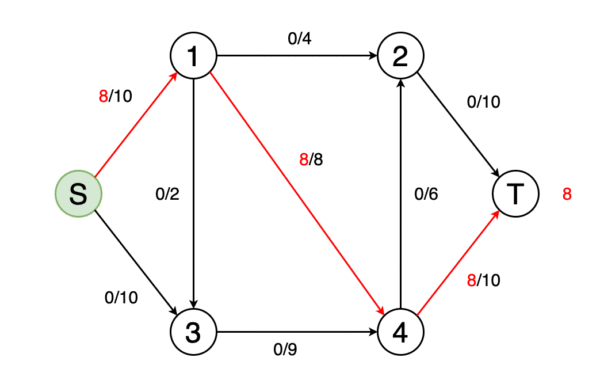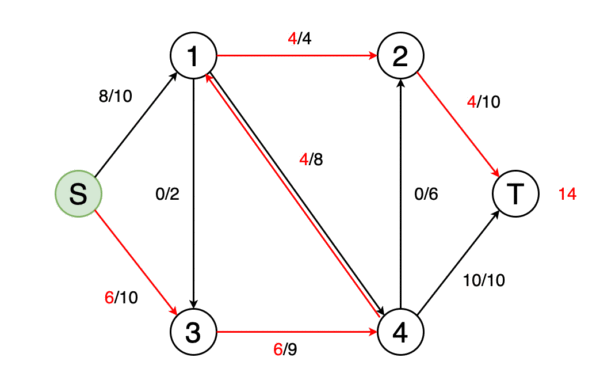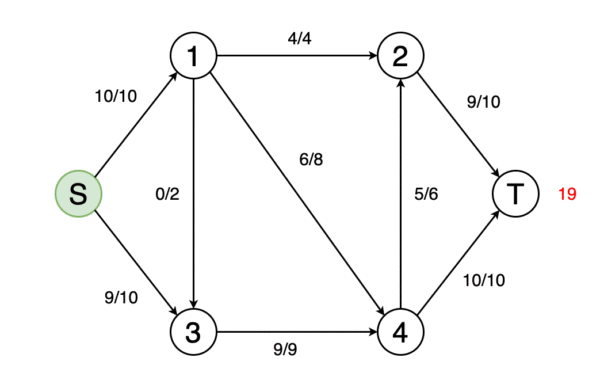
我們可以將圖建模為以邊權重為流量的流量網絡。 在最大流量問題中，我們必須找到一條可以獲得最大可能流量的流路。

圖10顯示了確定網絡的最大流量并確定最終流量值的動畫示例。

演算法

• 福特-福克森算法

• Edmonds–Karp算法

• Dinic的算法

應用領域

• 用于航空公司調度以調度飛行人員。

• 用于圖像分割以查找圖像中的背景和前景。

• 用于淘汰無法贏得足夠比賽來趕上其所在部門的領先者的棒球隊。

10.匹配

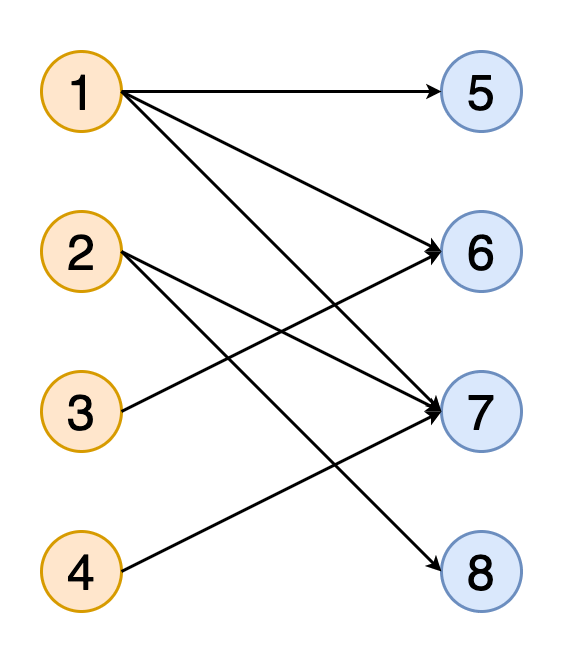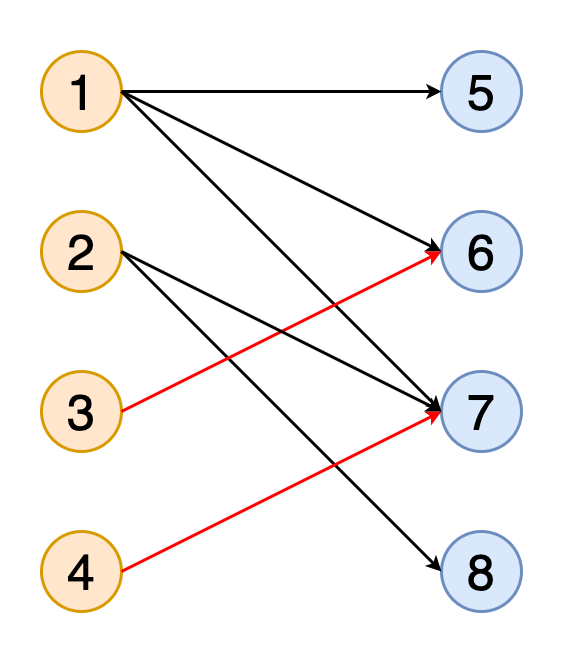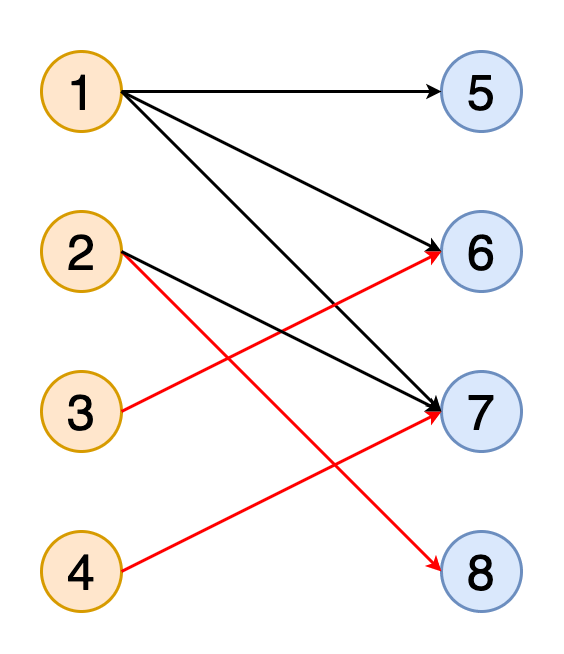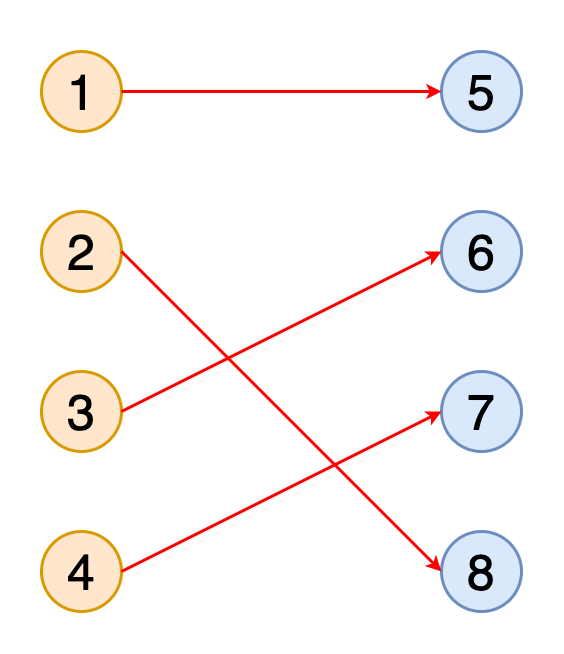
圖中的匹配項是一組沒有共同頂點的邊(即，沒有兩個邊共享共同的頂點)。 如果匹配包含盡可能多的與盡可能多的頂點匹配的邊，則該匹配稱為最大匹配。

圖11顯示了獲得二部圖與橙色和藍色表示的兩組頂點的完全匹配的動畫。

演算法

• Hopcroft-Karp算法

• 匈牙利算法

•  開花算法

應用領域

• 用于對接會以匹配新娘和新郎(穩定的婚姻問題)。

• 用于確定頂點覆蓋率。

• 在運輸理論中用于解決資源分配和出行優化中的問題。

“有哪些圖形算法”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站，小編將為大家輸出更多高質量的實用文章！