Python中怎么檢驗時間序列的平穩性

Python中怎么檢驗時間序列的平穩性，很多新手對此不是很清楚，為了幫助大家解決這個難題，下面小編將為大家詳細講解，有這方面需求的人可以來學習下，希望你能有所收獲。

首先我們還是來簡單介紹一下平穩性檢驗的相關概念。

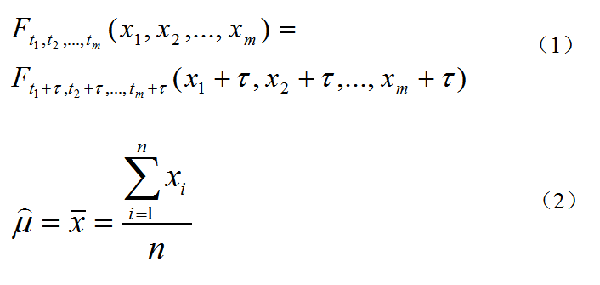
圖1. 平穩性序列的相關公式

時間序列的平穩性可分為嚴平穩和寬平穩。設{Xt}是一時間序列，對任意正整數m，任取t1、t2、t3、...、tm∈T，對任意整數τ，假如滿足圖1中式（1），則稱時間序列{Xt}是嚴平穩時間序列。而寬平穩的定義為，如果{Xt}滿足以下三個條件：

（1）任取t&isin;T，有E(Xt&middot;Xt)<&infin;；

（2）任取t&isin;T，有E Xt =&mu;，&mu;為常數；

（3）任取t，s，k&isin;T，且k+s-t&isin;T，有&gamma;(t, s)=&gamma;(k, k+s-t)

則稱{Xt}為寬平穩時間序列。

因為實際應用中我們很難獲得隨機序列的分布函數，所以嚴平穩用得極少，主要是使用寬平穩時間序列。

在了解了平穩性的基本概念之后，我們再來說一下平穩時間序列的意義。平穩時間序列的分析也遵循數理統計學的基本原理，都是利用樣本信息來推測總體信息。這就要求分析的隨機變量越少越好（也就是數據的維度越小越好），而每個變量獲得樣本信息越多越好（也就是數據的觀測值越大越好），因為隨機變量越少，分析過程越簡單，樣本容量越大，分析的結果越可靠。但時間序列的數據結構有其特殊性，它在任意時刻t的序列值Xt都是一個隨機變量，而且由于時間的不可重復性，該變量在任意一個時刻只能獲得唯一的樣本觀測值。由于樣本信息太少，如果沒有其他的輔助信息，這種數據結構通常是沒有辦法分析的，但序列平穩性就可以有效解決這個問題。在平穩序列中，序列的均值等于常數就意味著原本含有可列多個隨機變量的均值序列{&mu;t, t&isin;T}變成了一個常數序列{&mu;, t&isin;T}，原本每個隨機變量的均值&mu;t只能依靠唯一的一個樣本觀察值xt去估計，現在由于&mu;t=&mu;，于是每一個樣本觀察值xt，都變成了常數均值的樣本觀察值，如圖1中式（2）所示。這就極大減少了隨機變量的個數，并增加了待估參數的樣本容量，這也就降低了時序分析的難度。

在了解了時間序列的平穩性之后，我們再來詳細講解一下如何用python來進行檢驗。

用python來進行平穩性檢驗主要有3種方法，分別是時序圖檢驗、自相關圖檢驗以及構造統計量進行檢驗。

首先來說時序圖檢驗，時序圖就是普通的時間序列圖，即以時間為橫軸，觀察值為縱軸進行檢驗。這里筆者給出3個例子，因為時序圖過于簡單，所以筆者在這里直接用Excel作時序圖，用python也可以，不過沒有Excel簡單。第一個例子是1964-1999年中國紗年產量時間序列（該數據來自北京統計局），其數據如圖2所示，序列圖如圖3所示。圖3中明顯可以看出，中國紗年產量序列有明顯的遞增趨勢，所以它一定不是平穩序列。

圖2. 紗產量部分數據截圖

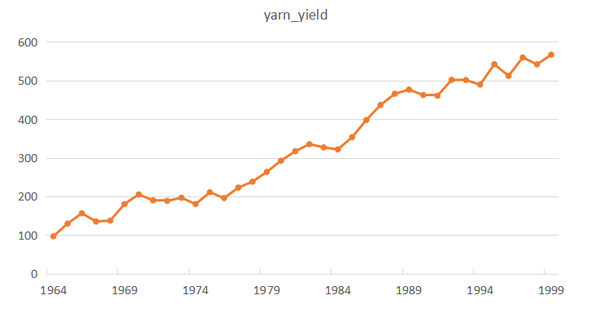
圖3. 紗產量時序圖

第二個例子是1962年1月至1975年12月平均每頭奶牛月產奶量時間序列（數據來自網站http://census-info.us），其數據如圖4所示，序列圖如圖5所示。從圖5中可以看出，平均每頭奶牛的月產奶量以年為周期呈規則的周期性，此外還有明顯的逐年遞增趨勢，所以該序列也一定不是平穩序列。

圖4. 奶牛產量部分數據截圖

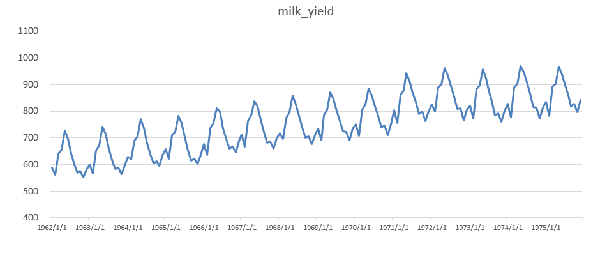
圖5. 奶牛產量時序圖

第三個例子是1949年至1998年北京市每年最高氣溫序列（數據來自北京市統計局），其數據如圖6所示，序列圖如圖7所示。從圖7中可以看出，北京市每年的最高氣溫始終圍繞在37度附近隨機波動，沒有明顯趨勢或周期，基本可以視為平穩序列，但我們還需要利用自相關圖進一步驗證。

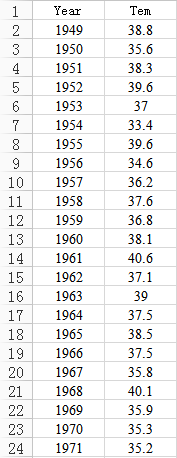
圖6. 北京最高氣溫部分數據截圖

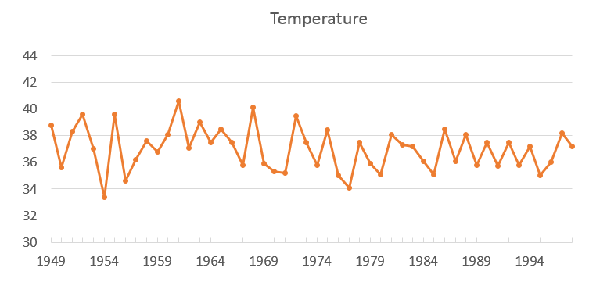
圖7. 北京最高氣溫時序圖

從上面的例子可以看出，時序圖只能粗略來判斷一個時間序列是否為平穩序列，我們可以用自相關圖來更進一步檢驗。要畫自相關圖，我們就要用到python，下面是相關代碼。

import pandas as pd  import matplotlib.pyplot as plt  from statsmodels.graphics.tsaplots import plot_acf  temperature = r'C:\Users\北京氣溫.xls'  milk = r'C:\Users\奶牛產量.xlsx'  yarn = r'C:\Users\紗產量.xls'  data_tem = pd.read_excel(temperature, parse_date=True)  data_milk = pd.read_excel(milk, parse_date=True)  data_yarn = pd.read_excel(yarn, parse_date=True)  plt.rcParams.update({'figure.figsize':(8,6), 'figure.dpi':100}) #設置圖片大小  plot_acf(data_tem.Tem) #生成自相關圖  plot_acf(data_milk.milk_yield)  plot_acf(data_yarn.yarn_yield)  plt.show()

畫自相關圖用到的是statsmodels中的plot_acf方法，這個方法很簡單，只需要直接輸入數據即可，不過數據要是一維的，生成的3張圖如圖8、圖9和圖10所示。

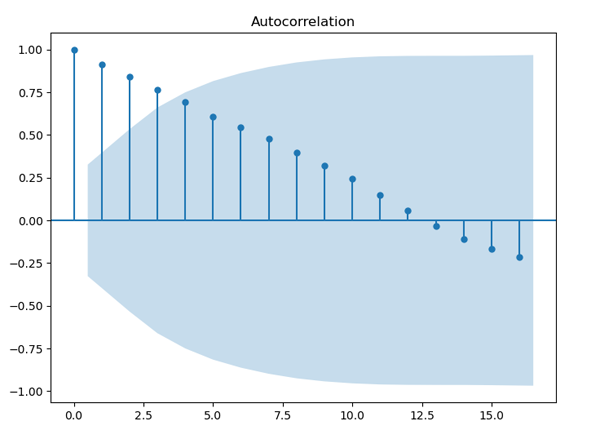
圖8. 紗產量自相關圖

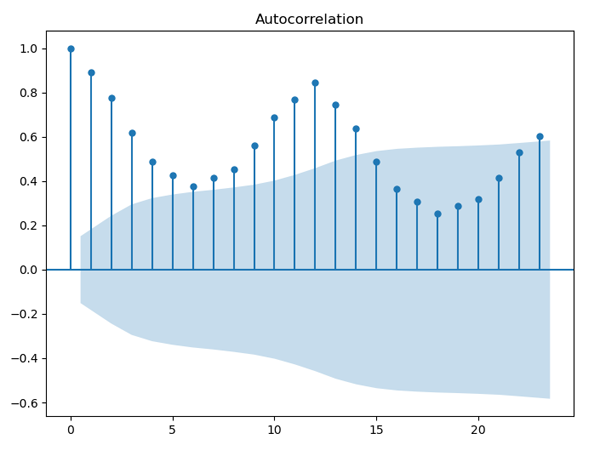
圖9. 奶牛產量自相關圖

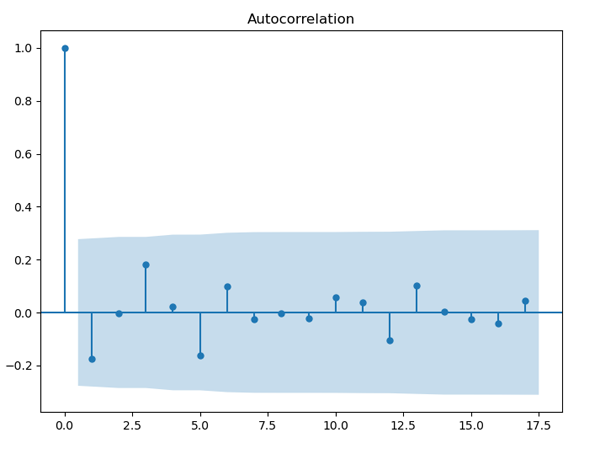
圖10. 北京最高氣溫自相關圖

平穩序列通常具有短期相關性，即隨著延遲期數k的增加，平穩序列的自相關系數會很快地衰減向零，而非平穩序列的自相關系數的衰減速度會比較慢，這就是我們利用自相關圖判斷平穩性的標準。我們就來看下這3張自相關圖，圖8是紗年產量的自相關圖，其橫軸表示延遲期數，縱軸表示自相關系數，從圖中可以看出自相關系數衰減到零的速度比較緩慢，在很長的延遲期內，自相關系數一直為正，然后為負，呈現出三角對稱性，這是具有單調趨勢的非平穩序列的一種典型的自相關圖形式。再來看看圖9，這是每頭奶牛的月產奶量的自相關圖，圖中自相關系數長期位于零軸一邊，這是具有單調趨勢序列的典型特征，同時還呈現出明顯的正弦波動規律，這是具有周期變化規律的非平穩序列的典型特征。最后再來看下圖10，這是北京每年最高氣溫的自相關圖，圖中顯示該序列的自相關系數一直比較小，可以認為該序列一直在零軸附近波動，這是隨機性較強的平穩序列通常具有的自相關圖。

最后我們再講一下ADF方法。前面兩種方法都是作圖，圖的特點是比較直觀，但不夠精確，而ADF法則是直接通過假設檢驗的方式來驗證平穩性。ADF（全稱Augmented Dickey-Fuller）是一種單位根檢驗方法，單位根檢驗方法比較多，而ADF法是比較常用的一種，其和普通的假設檢驗沒有太大區別，都是列出原假設和備擇假設。ADF的原假設（H0）和備擇假設（H1）如下。

H0：具有單位根，屬于非平穩序列。

H1：沒有單位根，屬于平穩序列，說明這個序列不具有時間依賴型結構。

下面我們就用python代碼來解釋一下ADF的用法。

from statsmodels.tsa.stattools import adfuller  yarn_result = adfuller(data_yarn.yarn_yield) #生成adf檢驗結果  milk_result = adfuller(data_milk.milk_yield)  tem_result = adfuller(data_tem.Tem)  print('The ADF Statistic of yarn yield: %f' % yarn_result[0])  print('The p value of yarn yield: %f' % yarn_result[1])  print('The ADF Statistic of milk yield: %f' % milk_result[0])  print('The p value of milk yield: %f' % milk_result[1])  print('The ADF Statistic of Beijing temperature: %f' % tem_result[0])  print('The p value of Beijing temperature: %f' % tem_result[1])

這里我們用的是statsmodels中的adfuller方法，其使用也比較簡單，直接輸入數據即可，但其返回值較多，返回的結果中共有7個值，分別是adf、pvalue、usedlag、nobs、critical values、icbest和resstore，這7個值的意義大家可以參考官方文檔，我們這里用到的是前兩個，即adf和pvalue，adf就是ADF方法的檢驗結果，而pvalue就是我們常用的p值。我們的得到結果如圖11所示。

看完上述內容是否對您有幫助呢？如果還想對相關知識有進一步的了解或閱讀更多相關文章，請關注億速云行業資訊頻道，感謝您對億速云的支持。